今天的第二道tarjan：受欢迎的牛

原题来自：USACO 2003 Fall

题目描述

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 AAA 喜欢 BBB，BBB 喜欢 CCC，那么 AAA 也喜欢 CCC。牛栏里共有 NNN 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入格式

第一行：两个用空格分开的整数：NNN 和 MMM。

接下来 MMM 行：每行两个用空格分开的整数：AAA 和 BBB，表示 AAA 喜欢 BBB。

输出格式

一行单独一个整数，表示明星奶牛的数量。

输入输出样例

输入 #1

3 3
1 2
2 1
2 3

输出 #1

1

说明/提示

只有 3 号奶牛可以做明星。

数据范围

 

 

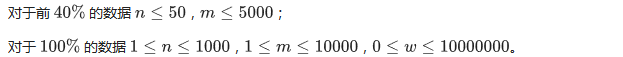
题解

emmmm

这是一到极为经典的，似乎是这一类题的模板的题目：缩点
缩点，也是tarjan的极大的一个作用。
缩点只对强联通分量有用，因为强联通分量中的点可以互相到达，可以被视为一个点。

这题，是肯定是有环的。
那么肯定是很不好去实现遍历的。
怎么办呢？
根据常识，环上的点肯定都在同一个强联通分量中。
强联通分量 -->缩点
经过缩点的图，一定是一个有向无环图
那么只需要一个dfs就好了啊awa
简单题
awa
淦，题解写完了，代码还没写。。。

等等我写完代码awa

 

#include<bits/stdc++.h>
#define ll long long
using namespace std;
struct edge
{
    int next,to;
}e[1000001];
int head[1000001],n,m,w[1000001],tot,ccs,dfsc,low[1000001],dfn[1000001],color[10000001],cnt[1000001],de[1000001],all[1000001];bool vis[1000001];
stack<int> stk;
inline ll read()
{
    char c=getchar();ll a=0,b=1;
    for(;c<'0'||c>'9';c=getchar())if(c=='-')b=-1;
    for(;c>='0'&&c<='9';c=getchar())a=a*10+c-48;
    return a*b;
}
void add(int i,int j)
{
    e[++tot].next=head[i];
    e[tot].to=j;
    head[i]=tot;
}
void tarjan(int x,int fa)
{
    dfn[x]=low[x]=++dfsc;
    vis[x]=true;stk.push(x);
    for(int i=head[x];i!=0;i=e[i].next)
    {
        int u=e[i].to;
//        if(u==fa)continue;
        if(dfn[u]==0)
        {
            tarjan(u,x);
            low[x]=min(low[x],low[u]);
        }
        else
        if(vis[u]==true)
        {
            low[x]=min(low[x],dfn[u]);
        }
    }
    if(dfn[x]==low[x])
    {
        int k;
        ccs++;
        do
        {
            k=stk.top();
            stk.pop();
            color[k]=ccs;
            cnt[ccs]++;all[ccs]++;
            vis[k]=false;
        }
        while(x!=k);
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read();m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read();int y=read();
        add(x,y);
    }
    for(int i=1;i<=n;i++)
    {
        if(dfn[i]==0)
        {
            tarjan(i,-1);
        }
    }
//    for(int i=1;i<=n;i++)
//    {
//        cout<<color[i]<<endl;
//    }
    for(int i=1;i<=n;i++)
    {
        int x=i;
        for(int j=head[x];j!=0;j=e[j].next) 
        {
            int u=e[j].to;
            if(color[u]!=color[x])
            {
                de[color[i]]++;
            }
        }
    }
    int ans=0,sum=0;bool tt=0;
    for(int i=1;i<=ccs;i++)
    {
        if(de[i]==0)
        {
            ans+=cnt[color[i]];
            sum++;
            if(tt){puts("0");return 0;}
            tt=i;
        }
    }
    cout<<all[tt]<<endl;
    return 0;
}

 n年前的草稿总算是发布了awa