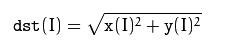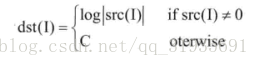C++ Opencv 傅里叶变换的代码实现及关键函数详解

一、前言

最近几天接触了图像的傅里叶变换，数学原理依旧不是很懂，因此不敢在这里妄言。下午用Opencv代码实现了这一变换，有一些经验心得，愿与大家分享。

二、关键函数解析

2.1copyMakeBorder() 扩展图片尺寸

傅里叶变换的计算对图像的尺寸有一定要求，尺寸不满足要求的，可用copyMakeBorder() 函数进行扩展。函数定义如下：

void copyMakeBorder(InputArray  src,        //输入图像
		    OutputArray dst,        //输出图像
		    int top,                //上边界添加的像素行数
		    int bottom,             //下边界添加的像素行数
		    int left,               //左边界添加的像素列数
		    int right,              //右边界添加的像素列数
		    int borderType,         //表示边界的类型
		    const Scalar& value=Scalar()//表示如果边界的类型是BORDER_CONSTANT时边界的颜色值 )

borderType边界的类型有以下几种:

1)BORDER_REPLICATE:重复： aaaaaa|abcdefgh|hhhhhhh

2)BORDER_REFLECT:反射: fedcba|abcdefgh|hgfedcb

3)BORDER_REFLECT_101:反射101: gfedcb|abcdefgh|gfedcba

4)BORDER_WRAP:外包装： cdefgh|abcdefgh|abcdefg

5)BORDER_CONSTANT:常量复制： iiiiii|abcdefgh|iiiiiii(i的值由最后一个参数 const Scalar& value=Scalar()确定，如Scalar::all(0) )

2.2getOptimalDFTSize() 获取最佳计算尺寸

离散傅里叶变换的计算速度与图片的尺寸有关，当图片的尺寸是2，3，5的倍数时，计算速度最快。常与函数copyMakeBorder() 配合使用，保证较快的计算速度。

int getOptimalDFTSize(int vecsize)

使用示例：

int m = getOptimalDFTSize(mImage.rows);//返回行的最佳尺寸
int n = getOptimalDFTSize(mImage.cols);//返回列的最佳尺寸
copyMakeBorder(mImage, mImage, 0, m - mImage.rows, 0, n - mImage.cols, BORDER_CONSTANT, Scalar(0));

2.3dft()傅里叶变换计算

傅里叶变换计算函数。

void dft(InputArray src, OutputArray dst, int flags=0, int nonzeroRows=0);

参数解释：
InputArray src: 输入图像，可以是实数或虚数
OutputArray dst: 输出图像，其大小和类型取决于第三个参数flags
int flags = 0: 转换的标识符，有默认值0。其可取的值如下所示：
1）DFT_INVERSE: 用一维或二维逆变换取代默认的正向变换；
2）DFT_SCALE: 缩放比例标识符，根据数据元素个数平均求出其缩放结果，如有N个元素，则输出结果以1/N缩放输出，常与DFT_INVERSE搭配使用；
3）DFT_ROWS: 对输入矩阵的每行进行正向或反向的傅里叶变换；此标识符可在处理多种适量的的时候用于减小资源的开销，这些处理常常是三维或高维变换等复杂操作；
4）DFT_COMPLEX_OUTPUT: 对一维或二维的实数数组进行正向变换，这样的结果虽然是复数阵列，但拥有复数的共轭对称性（CCS），可以以一个和原数组尺寸大小相同的实数数组进行填充，这是最快的选择也是函数默认的方法。你可能想要得到一个全尺寸的复数数组（像简单光谱分析等等），通过设置标志位可以使函数生成一个全尺寸的复数输出数组；
5）DFT_REAL_OUTPUT: 对一维二维复数数组进行逆向变换，这样的结果通常是一个尺寸相同的复数矩阵，但是如果输入矩阵有复数的共轭对称性（比如是一个带有DFT_COMPLEX_OUTPUT标识符的正变换结果），便会输出实数矩阵。
int nonzeroRows = 0: 当这个参数不为0，函数会假设只有输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值。这样的话函数就可以对其他的行进行更高效的处理节省一些时间，这项技术尤其是在采用DFT计算矩阵卷积时非常有效。

2.4magnitude()计算二维矢量幅值

void magnitude(InputArray x, InputArray y, OutputArray magnitude)；

参数解释：
InputArray x: 浮点型数组的x坐标矢量，也就是实部
InputArray y: 浮点型数组的y坐标矢量，必须和x尺寸相同
OutputArray magnitude: 与x类型和尺寸相同的输出数组
其计算公式如下：
这里写图片描述

2.5log()自然对数计算

log()函数的功能是计算每个数组元素绝对值的自然对数。

void log(InputArray src,OutputArray dst)

参数解释：

InputArray src：为输入图像
OutputArray dst：为得到的对数值

其原理如下：
这里写图片描述

2.6normalize()矩阵归一化

归一化就是把要处理的数据经过某种算法的处理限制在所需要的范围内。首先归一化是为了后面数据处理的方便，其次归一化能够保证程序运行时收敛加快。

void normalize(InputArray src, OutputArray dst, 
               double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray() )

参数解释：
InputArray src: 输入图像 ;
OutputArray dst: 输出图像，尺寸大小和src相同 ;
double alpha = 1: range normalization模式的最小值 ;
double beta = 0: range normalization模式的最大值，不用于norm normalization(范数归一化)模式 ;
int norm_type = NORM_L2: 归一化的类型，主要有 :
1)NORM_INF: 归一化数组的C-范数（绝对值的最大值）
2)NORM_L1: 归一化数组的L1-范数（绝对值的和）
3)NORM_L2: 归一化数组的L2-范数（欧几里得）
4)NORM_MINMAX: 数组的数值被平移或缩放到一个指定的范围，线性归一化，一般较常用。
int dtype = -1: 当该参数为负数时，输出数组的类型与输入数组的类型相同，否则输出数组与输入数组只是通道数相同，而depth = CV_MAT_DEPTH(dtype) ;
InputArray mask = noArray(): 操作掩膜版，用于指示函数是否仅仅对指定的元素进行操作。

归一化公式：

1)norm_type!=NORM_MINMAX(线性函数转换)：

if mask(i,j)!=0

dst(i,j)=(src(i,j)-min(src))*(b'-a')/(max(src)-min(src))+ a'

else

dst(i,j)=src(i,j)

其中b'=MAX(a,b), a'=MIN(a,b);

2)norm_type!=NORM_MINMAX:

if mask(i,j)!=0

dst(i,j)=src(i,j)*a/norm (src,norm_type,mask)

else

dst(i,j)=src(i,j)

其中，函数norm的功能是计算norm（范数）的绝对值

技术分享

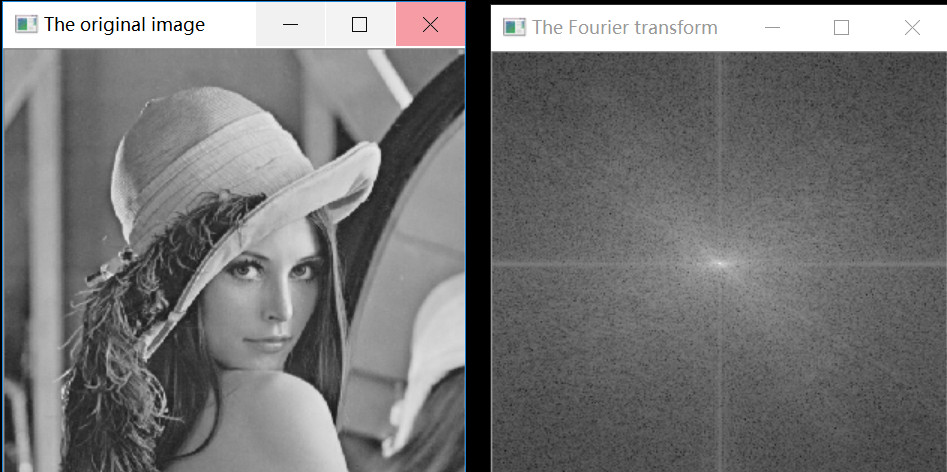
三、代码及结果分享

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace std;
using namespace cv;

int main() 
{
	Mat mImage = imread("Lenna.jpg", 0);
	if (mImage.data == 0)
	{
		cerr << "Image reading error" << endl;
		system("pause");
		return -1;
	}
	namedWindow("The original image", WINDOW_NORMAL);
	imshow("The original image", mImage);

	//Extending image
	int m = getOptimalDFTSize(mImage.rows);
	int n = getOptimalDFTSize(mImage.cols);
	copyMakeBorder(mImage, mImage, 0, m - mImage.rows, 0, n - mImage.cols, BORDER_CONSTANT, Scalar(0));

	//Fourier transform
	Mat mFourier(mImage.rows + m, mImage.cols + n, CV_32FC2, Scalar(0, 0));
	Mat mForFourier[] = { Mat_<float>(mImage), Mat::zeros(mImage.size(), CV_32F) };
	Mat mSrc;
	merge(mForFourier, 2, mSrc);
	dft(mSrc, mFourier);

	//channels[0] is the real part of Fourier transform,channels[1] is the imaginary part of Fourier transform 
	vector<Mat> channels;
	split(mFourier, channels);
	Mat mRe = channels[0];
	Mat mIm = channels[1];

	//Calculate the amplitude
	Mat mAmplitude;
	magnitude(mRe, mIm, mAmplitude);

	//Logarithmic scale
	mAmplitude += Scalar(1);
	log(mAmplitude, mAmplitude);

	//The normalized
	normalize(mAmplitude, mAmplitude, 0, 255, NORM_MINMAX);

	Mat mResult(mImage.rows, mImage.cols, CV_8UC1, Scalar(0));
	for (int i = 0; i < mImage.rows; i++)
	{
		uchar* pResult = mResult.ptr<uchar>(i);
		float* pAmplitude = mAmplitude.ptr<float>(i);
		for (int j = 0; j < mImage.cols; j++)
		{
			pResult[j] = (uchar)pAmplitude[j];
		}
	}

	Mat mQuadrant1 = mResult(Rect(mResult.cols / 2, 0, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant2 = mResult(Rect(0, 0, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant3 = mResult(Rect(0, mResult.rows / 2, mResult.cols / 2, mResult.rows / 2));
	Mat mQuadrant4 = mResult(Rect(mResult.cols / 2, mResult.rows / 2, mResult.cols / 2, mResult.rows / 2));

	Mat mChange1 = mQuadrant1.clone();
	//mQuadrant1 = mQuadrant3.clone();
	//mQuadrant3 = mChange1.clone();
	mQuadrant3.copyTo(mQuadrant1);
	mChange1.copyTo(mQuadrant3);

	Mat mChange2 = mQuadrant2.clone();
	//mQuadrant2 = mQuadrant4.clone();
	//mQuadrant4 = mChange2.clone();
	mQuadrant4.copyTo(mQuadrant2);
	mChange2.copyTo(mQuadrant4);

	namedWindow("The Fourier transform", WINDOW_NORMAL);
	imshow("The Fourier transform", mResult);
	waitKey();
	destroyAllWindows();
	return 0;
}

四、注意事项

4.1Mat对象类型问题

为方便运算，在计算过程中，Mat对象中数据都是float型，将其归一化至0-255范围后仍保留有小数部分，造成无法用imshow()正常显示。最后结果必须用uchar强制转换。源代码中以下片段实现了这一过程：

	normalize(mAmplitude, mAmplitude, 0, 255, NORM_MINMAX);

	Mat mResult(mImage.rows, mImage.cols, CV_8UC1, Scalar(0));
	for (int i = 0; i < mImage.rows; i++)
	{
		uchar* pResult = mResult.ptr<uchar>(i);
		float* pAmplitude = mAmplitude.ptr<float>(i);
		for (int j = 0; j < mImage.cols; j++)
		{
			pResult[j] = (uchar)pAmplitude[j];
		}
	}

4.2clone()与copyTo()的差异问题

clone 是完全的深拷贝，在内存中申请新的空间。copyTo 也是深拷贝，但是否申请新的内存空间，取决于dst矩阵头中的大小信息是否与src一至，若一致则只深拷贝并不申请新的空间，否则先申请空间后再进行拷贝。

Mat A  = Mat::ones(4,5,CV_32F);
Mat B = A.clone()    //clone 是完全的深拷贝，在内存中申请新的空间，与Ａ独立
Mat C;
A.copyTo(C) //此处的Ｃ矩阵大小与Ａ大小不一致，则申请新的内存空间，并完成拷贝，等同于clone()
Mat D = A.col(１);
A.col(0).copyTo(D)　//此处D矩阵大小与Ａ.col(0)大小一致，因此不会申请空间，而是直接进行拷贝，相当于把Ａ的第１列赋值给第二列

因此在进行不同象限数据对换时，用copyTo()能成功对换数据，而用clone()则不能起到作用，原因就在于mQuadrant.clone()时重新开辟了内存空间，数据对换时对换的并非是原矩阵mResult中的数据。所以源代码中，以下片段能够正常对换数据，而注释掉的部分不能正常工作。

	Mat mChange1 = mQuadrant1.clone();
	//mQuadrant1 = mQuadrant3.clone();
	//mQuadrant3 = mChange1.clone();
	mQuadrant3.copyTo(mQuadrant1);
	mChange1.copyTo(mQuadrant3);

	Mat mChange2 = mQuadrant2.clone();
	//mQuadrant2 = mQuadrant4.clone();
	//mQuadrant4 = mChange2.clone();
	mQuadrant4.copyTo(mQuadrant2);
	mChange2.copyTo(mQuadrant4);

注：错误之处，敬请雅正！

posted @ 2018-07-24 19:30 秋沐霖阅读(8968) 评论(1) 编辑收藏举报

刷新页面返回顶部