Splay

注：本文改自http://blog.csdn.net/changtao381/article/details/8936765与百度百科伸展树。

（代码为本人原创，有两百多行，第一次很难写，但是写多了就好了。）

博客原作者若有问题可联系本人（815344231@qq.com），多谢。

类别：二叉排序树

空间效率：O(n)
时间效率：O(log n)内完成插入、查找、删除操作

创造者：Daniel Sleator和Robert Tarjan

优点：每次查询会调整树的结构，使被查询频率高的条目更靠近树根。

注：所有图片来自wiki——http://en.wikipedia.org/wiki/Splay_tree（English）。

Tree Rotation

 

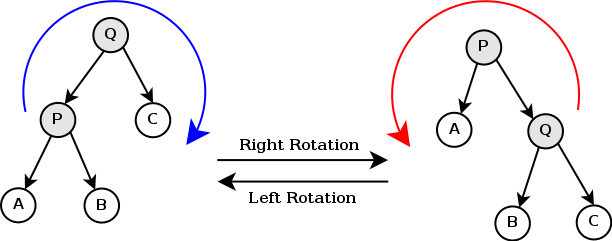
树的旋转是splay的基础，对于二叉查找树来说，树的旋转不破坏查找树的结构。

 

Splaying

 

Splaying是Splay Tree中的基本操作，为了让被查询的条目更接近树根，Splay Tree使用了树的旋转操作，同时保证二叉排序树的性质不变。

Splaying的操作受以下三种因素影响：

• 节点x是父节点p的左孩子还是右孩子
• 节点p是不是根节点，如果不是
• 节点p是父节点g的左孩子还是右孩子

同时有三种基本操作：

 

Zig Step

当p为根节点时，进行zip step操作。

当x是p的左孩子时，对x右旋；

当x是p的右孩子时，对x左旋。

 

Zig-Zig Step

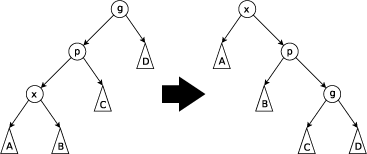
当p不是根节点，且x和p同为左孩子或右孩子时进行Zig-Zig操作。

当x和p同为左孩子时，依次将p和x右旋；

当x和p同为右孩子时，依次将p和x左旋。

 

 

Zig-Zag Step

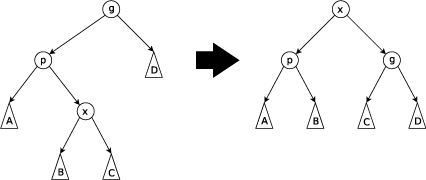
当p不是根节点，且x和p不同为左孩子或右孩子时，进行Zig-Zag操作。

当p为左孩子，x为右孩子时，将x左旋后再右旋。

当p为右孩子，x为左孩子时，将x右旋后再左旋。

 

其余操作

查找操作

 Find(x,S)：判断元素x是否在伸展树S表示的有序集中。

首先，与在二叉查找树中的查找操作一样，在伸展树中查找元素x。如果x在树中，则再执行Splaying(x,S)调整伸展树。

加入操作

 Insert(x,S)：将元素x插入伸展树S表示的有序集中。

首先，也与处理普通的二叉查找树一样，将x插入到伸展树S中的相应位置上，再执行Splaying(x,S)。

删除操作

 Delete(x,S)：将元素x从伸展树S所表示的有序集中删除。

首先，用在二叉查找树中查找元素的方法找到x的位置。如果x没有孩子或只有一个孩子，那么直接将x删去，并通过Splaying操作，将x节点的父节点调整

到伸展树的根节点处。否则，则向下查找x的后继y，用y替代x的位置，最后执行Splaying(y,S)，将y调整为伸展树的根。

合并操作

 join(S1,S2)：将两个伸展树S1与S2合并成为一个伸展树。其中S1的所有元素都小于S2的所有元素。首先，我们找到伸展树S1中最大的一个元素x，再通过Splaying(x,S1)将x调整到伸展树S1的根。然后再将S2作为x节点的右子树。这样，就得到了新的伸展树S。

划分操作

 Split(x,S)：以x为界，将伸展树S分离为两棵伸展树S1和S2，其中S1中所有元素都小于x，S2中的所有元素都大于x。首先执行Find(x,S)，将元素x调整为伸展树的根节点，则x的左子树就是S1，而右子树为S2。

其他操作

 除了上面介绍的五种基本操作，伸展树还支持求最大值、求最小值、求前趋、求后继等多种操作，这些基本操作也都是建立在伸展操作的基础上的。

通常来说，每进行一种操作后都会进行一次Splaying操作，这样可以保证每次操作的平摊时间复杂度是O(logn)。

 

 

代码

#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>
using namespace std;
#define N 100000
struct Tree
 {
     int Le,Ri,Fa,s;
 };
Tree a[N];
int n=0,Gf=0;
void RiTn(int x)//右旋
 {
     int i=a[a[x].Fa].Fa;
     if (i==0)
      Gf=i;else
      {
          if (a[i].Le==a[x].Fa)
            a[i].Le=x;else
            a[i].Ri=x;
      }
     if (a[x].Ri!=0)
       a[a[x].Ri].Fa=a[x].Fa;
     a[a[x].Fa].Le=a[x].Ri;
     a[a[x].Fa].Fa=x;
     a[x].Ri=a[x].Fa;
     a[x].Fa=i;
     return;
 }
void LeTn(int x)//左旋
 {
     int i=a[a[x].Fa].Fa;
     if (i==0)
      Gf=i;else
      {
          if (a[i].Le==a[x].Fa)
            a[i].Le=x;else
            a[i].Ri=x;
      }
     if (a[x].Le!=0)
       a[a[x].Le].Fa=a[x].Fa;
     a[a[x].Fa].Ri=a[x].Le;
     a[a[x].Fa].Fa=x;
     a[x].Le=a[x].Fa;
     a[x].Fa=i;
     return;
 }
int Find(int x,int y)//查找元素
 {
     if (y==0) 
      return 0;
     if (a[y].s==x) 
      return y;else
       if (a[y].s>x) 
        return Find(x,a[y].Le);else
         return Find(x,a[y].Ri);
 }
void Insert(int x)//插入操作
 {
     if (a[n].s<a[x].s)
      {
          if (a[x].Le==0)
            {
                a[x].Le=n;
                a[n].Fa=x;
           }else 
          Insert(a[x].Le);
      }else
      {
          if (a[x].Ri==0)
            {
                a[x].Ri=n;
                a[n].Fa=x;
            }else 
          Insert(a[x].Ri);
      }
     return;
 }
int Fnext(int x)//查找后继
 {
     if (a[x].Le==0) 
      return x;else
       return Fnext(a[x].Le);
 }
int main()
 {
     int i,j,k,l,q,w,e,m;
     string b;
     scanf("%d",&m);
     for (i=1;i<=m;i++)
      {
          cin >>b;
          if (b=="Find")
           {
               scanf("%d",&k);
            l=Find(k,Gf);
               if (l>0) 
                 {
                 printf("Yes\n");
                    while (Gf!=l) 
                  if (l==a[a[l].Fa].Le)
                    RiTn(l);else
                    LeTn(l);
              }else
                 printf("No\n");
           }else
          if (b=="Insert")
           {
               scanf("%d",&k);
               n++;
               a[n].s=k;
            a[n].Fa=0;
            a[n].Le=0;
            a[n].Ri=0;
               if (n==1) 
              Gf=1;else
                 {
                     Insert(Gf);
                     while (Gf!=n) 
                  if (a[a[n].Fa].Le==n)
                    RiTn(n);else
                    LeTn(n);
                 }
           }else
          if (b=="Delete")
           {
               scanf("%d",&k);
               l=Find(k,Gf);
               if (l==0) continue;
               if (a[l].Le*a[l].Ri==0)
                {
                    if (l!=Gf)
                  {
                     if (a[a[l].Fa].Ri==l)
                       a[a[l].Fa].Ri=a[l].Ri+a[l].Le;else
                           a[a[l].Fa].Le=a[l].Ri+a[l].Le;
                     }else 
                     Gf=a[l].Le+a[l].Ri;
                    if (a[l].Le>0)
                      a[a[l].Le].Fa=a[l].Fa;else
                      if (a[l].Ri>0)
                        a[a[l].Ri].Fa=a[l].Fa;
                a[l].Fa=0;
                a[l].Le=0;
                a[l].Ri=0;
                a[l].s=0;
                }else 
                {
                   q=Fnext(a[l].Ri);
                   if (q==a[a[q].Fa].Le)
                  {
                      a[a[q].Fa].Le=a[q].Ri;
                      if (a[q].Ri!=0) 
                      a[a[q].Ri].Fa=a[q].Fa;
                      if (l!=Gf)
                      {
                         if (l==a[a[l].Fa].Ri) 
                           a[a[l].Fa].Ri=q;else
                           a[a[l].Fa].Le=q;
                      }else
                      Gf=q;
                    a[q].Ri=a[l].Ri;
                    a[q].Fa=a[l].Fa;
                    a[q].Le=a[l].Le;
                    if (a[l].Le>0)
                      a[a[l].Le].Fa=q;
                    a[a[l].Ri].Fa=q;
                  }else
                  {
                      if (l!=Gf)
                      {
                         if (l==a[a[l].Fa].Le)
                             a[a[l].Fa].Le=q;else
                             a[a[l].Fa].Ri=q;
                      }else
                      Gf=q;
                      a[q].Fa=a[l].Fa;
                      a[q].Le=a[l].Le;
                      if (a[q].Le>0) a[a[q].Le].Fa=q;
                  }
                a[l].Fa=0;
                a[l].Le=0;
                a[l].Ri=0;
                a[l].s=0;
                }
           }
      }
     return 0;
 }

 

 

应用

 

Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。

每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。

对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。

对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。

这样，大部分区间问题都可以很方便的解决，操作同样也适用于一个或多个条目的添加或删除，和区间的移动。