多样性计算的各种距离
Beta多样性和生态相似性
Beta多样性(β多样性,Beta diversity),即在一个梯度上从一个生境到另一个生境所发生的种的多样性变化的速率和范围,它是研究群落之间的种多度关系。Beta多样性本身代表了一个复杂的问题,可以被视为物种更替(物种沿空间、时间或环境梯度的定向过程)或物种组成的差异(数据集内物种组成的异质性的非定向过程)。
下图展示了Alpha多样性、Beta多样性和Gamma多样性的关系(点击查看原文献)。图示三个群落,Alpha多样性反映了各群落内物种的丰富度、均匀度等,Beta多样性反映了群落间的差异水平,Gamma多样性可视为区域内Alpha多样性和Beta多样性的结合。
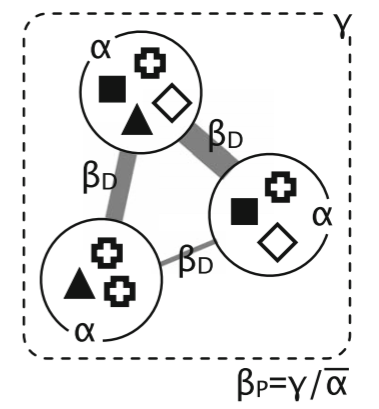
在群落的Beta多样性分析中,通常涉及到非约束排序(如PCA、PCoA等)、层次聚类(如UPGMA等)等具体的分析。关于这些具体的分析方法,本文不作阐述。无论哪种形式的Beta多样性分析,均以群落相似(或相异)程度为基础。
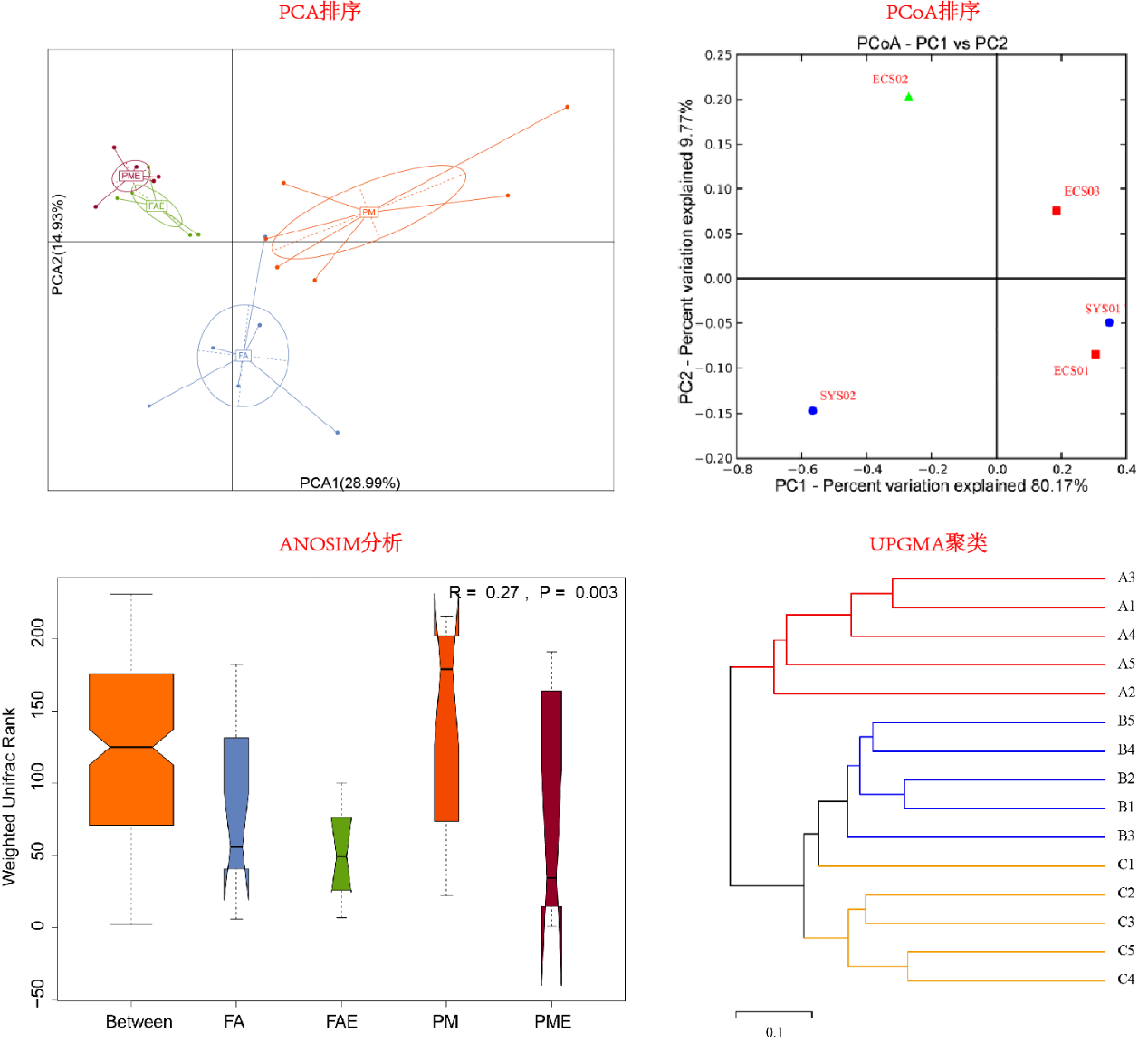
生态相似性(Ecological resemblance)以计算样方之间的群落组成相似程度或距离(相异程度)为基础,是处理多元生态数据的基本方法之一。在群落数据的分析中,常用其反映Beta多样性。如在物种数据的分析中,对于两个群落,若它们共享相同的物种,并且所有物种的丰度也一致,那么这两个群落就具有最高的相似程度(或最低距离0)。关于“相似性”和“距离”的概念详见下文。随着群落物种组成差异(种类和丰度)的增加,相似性逐渐降低,距离逐渐递增。
生态学数据分析中的很多统计方法都以样方之间的相似性或距离为基础,例如上述提到的Beta多样性分析中的聚类、排序等,即使对于PCA和CA,实质上在计算时也分别基于欧几里得(euclidean)和卡方(chi-square)距离考虑的。
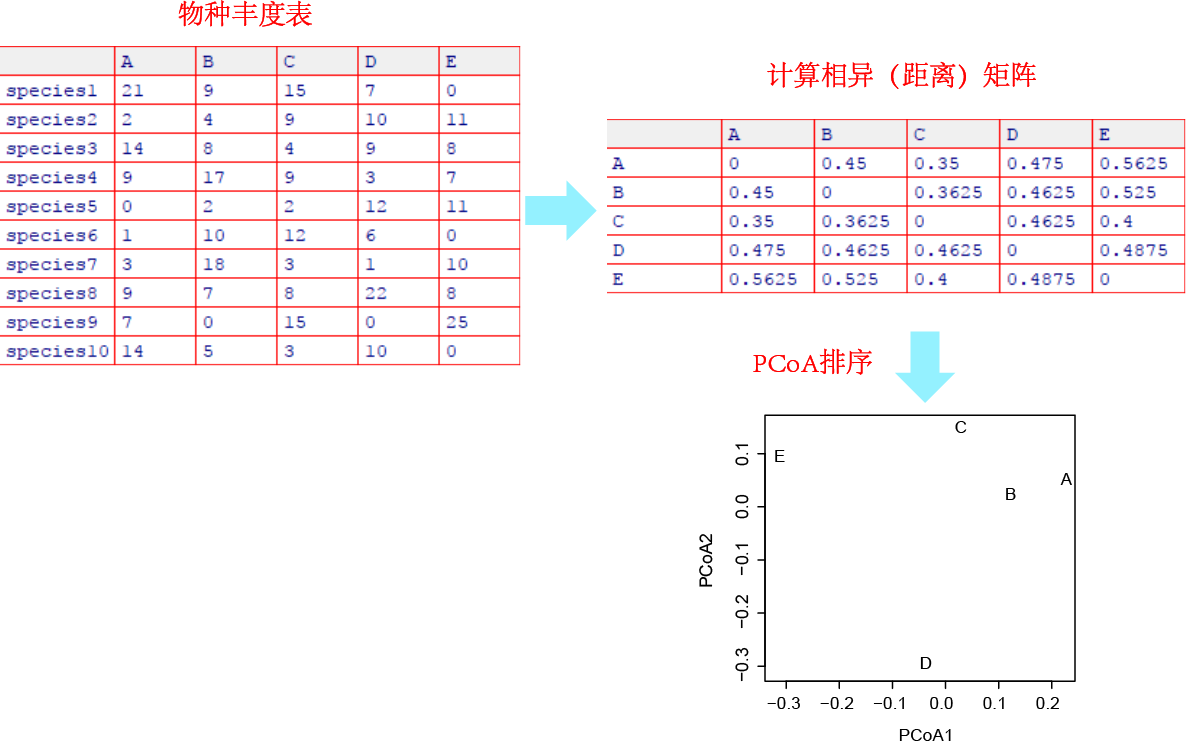
双零问题
在介绍“相似性”或“距离”之前,首先需要明确一个概念,“双零”。“双零”是指在计算群落相似性(或距离)时,所比较的两个样方中缺失某些物种的情况,这是很常见的现象。对于某些特定物种来讲,它们在两个样方中同时缺失的可能原因:
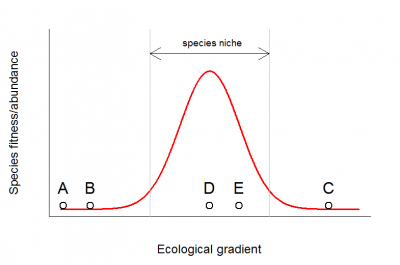
(1)两个样方位于这些物种生态位之外,但无法确定两个样方是否均处于生态梯度的同一侧(即它们是生态相似的,如下图所示的A、B两个样方),或者它们分别处于生态梯度的两侧(如下图所示的A、C两个样方,它们实际上存在非常大的差异)。
(2)样方位于物种生态位内(如下图所示的D、E两个样方),但是未被观测到。未被观测到的原因,可能是该物种恰好没有在我们所调查的区域出现(扩散限制),也可能仅仅由于采样误差而未被收集到,或者由于丰度太低而被忽视等。
在这两种情况下,双零代表了信息的缺失,限制了我们对生态群落的比较和深入研究。
这里有两个关键点:
(1)在大多数情况下,一个物种在两个样方内同时缺失,并不能成为这两个样方具有组成相似的依据,因为引起缺失的原因可能完全不同。
(2)在物种矩阵内,不可解释的双零的数量取决于物种的数量,因此也会随着检测到的稀有种数量的增加而显著增加。
因此,物种存在的信息比物种缺失的信息有更明确的意义。
相似性和距离
直观地理解,若两个对象在各属性上越近似,那么它们的相似性就越高。对于群落数据,这些属性一般就是物种组成,或者环境属性等。通常使用物种组成数据,依据相似性指数(similarity indices)判断群落相似性,范围由0(两个群落不共享任何物种)到1(两个群落的物种类型和丰度完全一致)。
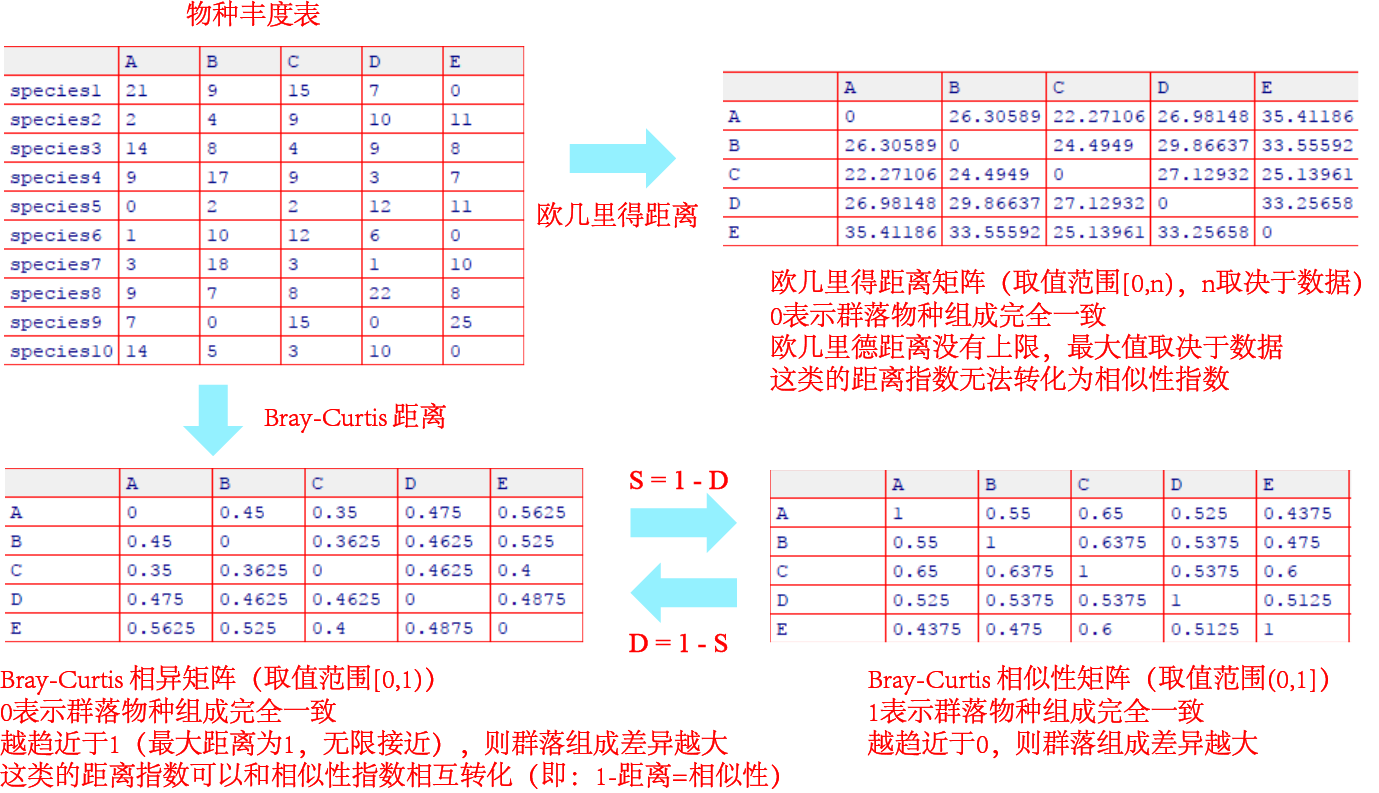
距离指数(distance indices)或称距离测度(distance measures),与相似性指数相反,距离数值越大表明群落间差异越大。存在多种距离类型,例如欧几里得(Euclidean)距离、Bray-Curtis距离、UniFrac距离等。对于物种组成数据,距离指数的最小值为0(两个群落的物种类型和丰度完全一致),最大取值取决于距离类型和数据本身。
在两个比较样方相同(最大相似)的情况下,相似性指数返回最高值;类似地,对于不共享任何物种的两个样方,距离指数最大。
相似性和距离的相互转换
所有相似性指数均可以转换为距离指数,转化公式大致就是“距离指数 = 1 – 相似性指数”的关系,因此不必多说。
但反过来,并非所有距离指数都可以转换为相似性指数:
(1)可以转化为相似性指数的距离指数,例如定量数据的相异百分率(也称为Bray-Curtis距离)等。二者相互转换的公式通常表示为D = 1-S或S = 1-D,其中S是相似性指数,D为距离指数。
(2)无法转化为相似性指数的距离指数,例如欧几里得距离、卡方距离。
对称指数和非对称指数
无论距离指数或相似性指数,可归为对称指数和非对称指数两种,它们在对于如何处理双零问题方面存在差异。对称指数(symmetrical indices)以双重存在相同的方式处理双零问题,即作为考虑样本相似的原因。这通常对物种组成数据没有意义;非对称指数(asymmetrical indices)忽略双零,在评估相似性时仅关注存在的部分,这些指数通常对物种组成数据更有意义。
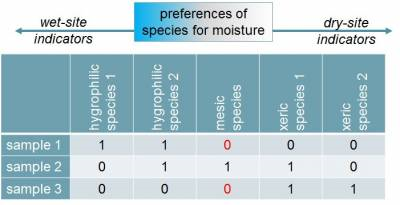
下图以一示例展示两种类型的指数在处理双零现象时的区别。由环境样品1至3,环境中的湿度依次降低。对于样品1和3,未观测到包含相同物种的存在,特别是对于“mesic species”这个物种来讲,产生“双零”。缺失物种的事实并没有说明两个样本之间的生态相似性或差异,因此最好忽略它。在对称指数的情况下,样品1和样品3中不存在的物种“mesic species”(0-0)会被考虑在内,这将增加样品1和3的相似性(或着说降低差异); 而在非对称指数中,样品1和样品3中均不存在的物种“mesic species”将被忽略,只考虑(至少有一个)存在情形(1-1,1-0,0-1)。相较之下,非对称指数的处理方式更为合理。
特别是在实际的分析中,由于涉及的群落数据很多,会存在大量的双零现象。因此,在群落物种数据的分析中,通常不建议使用对称指数(即那些认为双零相关的指数),因为它们可能会带来较大的误差(如上所述,在群落物种组成数据时无法很好地处理双零问题)。对于非对称指数(即忽略双零的那些),根据它们使用的数据,可分为两种类型:定性(二元)指数,应用于存在缺失数据;以及应用于原始(或转化)物种丰度的定量指数。当存在多样方时,其计算结果常用于反映群落Beta多样性。
尽管如此,在生态学数据分析中,对称指数并非显得“毫无用途”,实际上,它们在处理环境变量数据(变量属性为“环境”,而非“物种”)时可能是适用的。例如,对于包含化学测量的多变量数据。假设我们采集了多个环境中的土壤样本,意在比较土壤的受污染情况,在通过测量多种化学指标后,发现在其中两个样品中均未检测到重金属Hg存在(Hg在其他样本中是存在的,因此Hg在这两个样本中视为“双零”),此时Hg的缺失是需要如实考虑在内的,即“双零”反映了这两个样品之间的相似性。
相似性或距离的计算
相似性或距离的衡量标准有很多种,Legendre和Legendre(1998)列出大约30种方法,并对生态相似性作了更详细的介绍,有兴趣可自行参阅Legendre和Legendre(1998)“Numerical Ecology”第七章“Ecological resemblance”的内容。
下文简介其中几种常见的相似性指数及距离指数。
定性(二元)对称相似性指数、定量对称相似性指数
这种类型的相似性指数不适用于生态学数据分析,忽略。
定性(二元)非对称相似性指数
常见以下几种类型。
Jaccard相似性指数(Jaccard similarity index)将两个样方共享的物种数量(a)除以两个样方中出现的所有物种的总和(a + b + c,其中b和c是仅在第一个和第二个样方中出现的物种数量)。计算公式如下:

转换为Jaccard相异度(Jaccard dissimilarity):

与此相比,Sørensen相似性指数(Sørensen similarity index)认为两个样方之间共享的物种数量更重要,因此它计算两次。计算公式如下:

转换为Sørensen相异度(Sørensen dissimilarity):

在两个样方的物种丰富度指数差异很大的情况下(即一个样方比另一个样方具有更多的物种),Simpson相似性指数(Simpson similarity index)更为适用。在这种情形下,如果使用Jaccard或Sørensen相似性指数,它们的值通常非常低,因为会出现分母过大的情况(具有很多的非共享物种,特别是高物种丰富度的样方所贡献)导致指数的总值过低。Simpson相似性指数通过从分数b和c中仅取较小的数据来消除这个问题。计算公式如下:

转换为Simpson相异度(Simpson dissimilarity):

注意:这里的Simpson相似性指数(或Simpson相异度),不同于Alpha多样性指数中的Simpson指数。
定量非对称相似性指数
例如相似百分率(Percentage similarity),由“1 - 相异百分率”获得(即直接通过“1 – 距离指数 = 相似性指数”转化),相异百分率又称Bray-curtis距离,详见下文“Bray-curtis距离”。
欧几里得距离(Euclidean distance)
欧几里得距离是多变量分析中经常使用的一种距离,如在线性排序方法PCA、RDA,以及某些层次聚类算法中。欧几里得距离没有上限,最大值取决于数据。
欧几里得距离计算公式如下:

其中,y1j和y2j分别是对象1和2中元素j的数值。若是群落物种数据,那么y1j和y2j即分别是样方1和2中物种j的丰度。p是物种数(样方-物种矩阵中的物种数)。如下展示了仅包含两个物种的两个群落之间的欧几里得距离的计算过程。
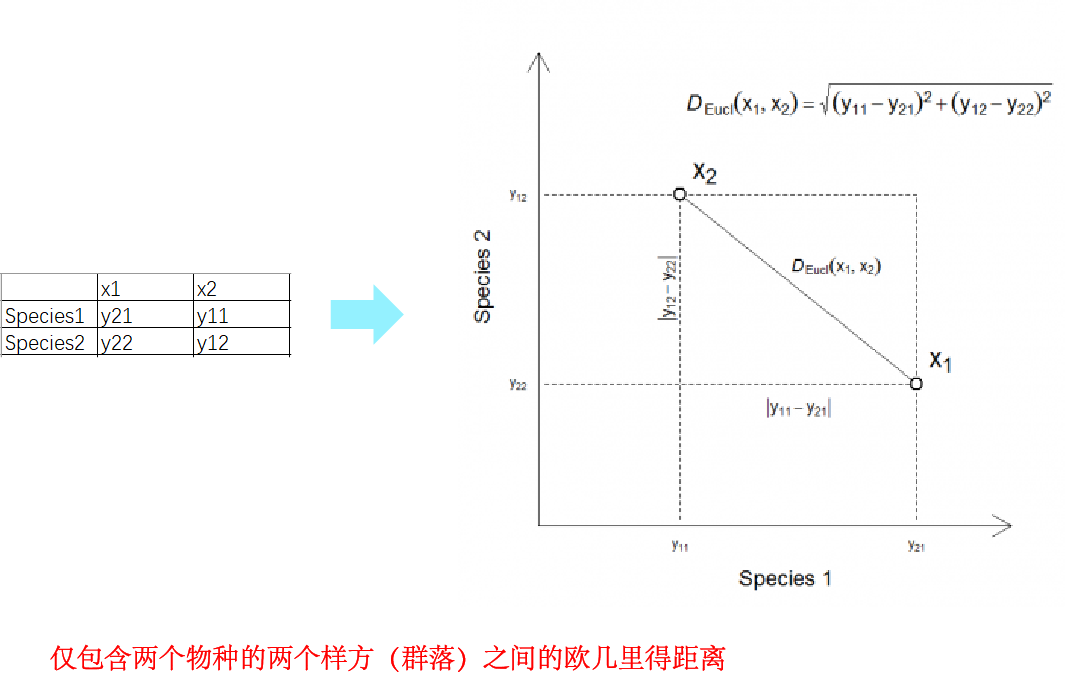
毫无疑问,作为最常规的距离之一,现实中欧几里得距离应用十分广泛。在生态学分析中,可以使用它来处理地理因素、环境指标、生物性状等数据。
但是在物种数据的分析中,欧几里得距离却表现得不很理想。主要原因在于它是一个对称的指数,即它将“双零”现象视作相同存在的方式处理,因此会缩小两个共享很少物种的群落之间的距离(实际上,它们差异很大)。可参考上文“对称指数和非对称指数”所述。并且,他还有对“物种丰度的差异”比对“物种是否存在”更加敏感的这么一个特点,也会影响我们对群落相似程度的判断。本文的末尾,详细展示了一例在物种数据处理中使用欧几里得距离可能会带来的问题。
如果仍要将欧几里得距离应用在物种数据的分析中,常见的解决方法是首先对原始物种数据执行预转化(常见的如弦转化、Hellinger转化等),然后再使用转化后的数据计算欧几里得距离(即对应于下文提到的弦距离、Hellinger距离,事实上,它们仍然属于欧氏距离)。尽管弦距离、Hellinger距离等然是对称指数的范畴,但是相较于使用原始物种丰度数据所得的欧几里得距离,弦距离、Hellinger距离的优势体现在存在距离的“上限”,降低了欧几里得距离对“物种丰度”的敏感性,有效减少了“双零”问题导致的误差。
更多情况下,我们在处理物种数据时,会尽可能避开使用欧几里得距离这类的对称指数。例如,通常我们选择使用非对称的Bray-curtis距离等。除非特定需要,不得不使用欧氏距离的情况下,可再考虑先转化数据再求欧几里得距离的方法。
弦距离(Chord distance)
弦距离是根据范数标准化的物种数据计算的欧几里得距离(首先对原始物种丰度数据执行范数标准化,又称为弦转化,再使用弦转化后的物种数据计算欧几里得距离,即为弦距离)。
弦转化意味着多维空间中的物种向量具有单位长度(对于每个样方,物种丰度平方和为1)。相较于使用原始物种数据直接计算的欧几里得距离(没有上限),弦距离具有上限(上限2^0.5)。
弦距离公式如下:

其中,y1j和y2j分别是对象1和2中元素j的数值。若是群落物种数据,那么y1j和y2j即分别是样方1和2中物种j的丰度。p是物种数(样方-物种矩阵中的物种数)。
Hellinger距离(Hellinger distance)
Hellinger距离是指通过Hellinger转化后物种数据计算的欧几里得距离(首先对原始物种丰度数据执行Hellinger转化,再使用转化后的物种数据计算欧几里得距离)。相较于使用原始物种数据直接计算的欧几里得距离(没有上限),Hellinger距离具有上限(上限2^0.5)。
对于样方i中物种j,执行Hellinger转化公式如下:

其中,yij是样方i中物种j的丰度,yi+是样方i中所有物种的丰度之和,y’ij是样方i中物种j的Hellinger转化后的丰度。从公式可以清楚地看出,它消除了样方间绝对丰度的差异(标准化为相对丰度),且平方根降低了优势物种的重要性。
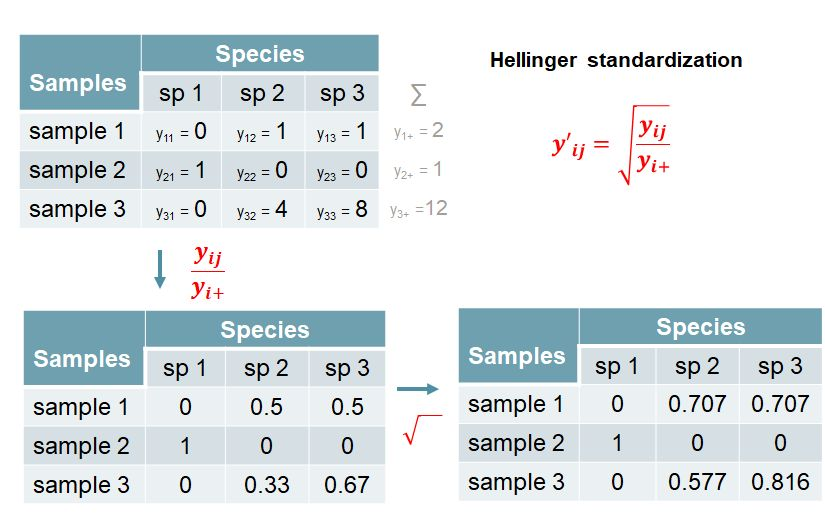
之后,再基于Hellinger转化后的数据计算的欧几里得距离,即为Hellinger距离。
因此Hellinger距离公式可直接写为:

其中,y1j和y2j分别是样方1和2中物种j的丰度,p是物种数(样方-物种矩阵中的物种数)。
Hellinger转化的另一种说法是平方根转化后的弦转化,反过来说,弦转化是多度数据平方后的Hellinger转化。这种关系表明弦距离和Hellinger距离存在关联。
Hellinger转化是一种预先转化物种组成数据以用于线性排序方法的方法,并且被认为是处理带有很多零值的生态数据的合适方法之一。例如,Hellinger距离常应用于物种数据的PCA、RDA等分析中(tb-PCA、tb-RDA),可有效避免“马蹄形效应”的产生(见本文末尾所述)。
卡方距离(chi-square distance)
卡方距离通常应用于单峰模型的排序方法中,如CA、CCA。
Bray-curtis距离(Bray-curtis distance)
Bray-curtis距离或称Bray-curtis相异度(Bray-curtis dissimilarity)、相异百分率(Percentage difference)。其计算公式如下:

其中p是物种数(样方-物种矩阵中的物种数),yij和yik表示两个样方中对应的物种多度。
Bray-curtis距离的取值范围范围由0(两个群落的物种类型和丰度完全一致)到1(两个群落不共享任何物种),因此它也可以直接通过“1 – 距离指数 = 相似性指数”转化为相似性指数(上文提到的“相似百分率”)。Bray-curtis距离适用于群落物种数据分析的原因在于它是一个非对称指数,可有效忽略双零。
Unifrac距离(Unifrac distance)
这里再额外简介一种特殊的距离,Unifrac距离,它常用于微生物群落的研究中(例如,16S扩增子测序)。上述距离的计算方法,仅考虑了物种的存在与否及其丰度,没有考虑物种之间的进化关系,距离0表示两个群落的物种组成结构完全一致。在Unifrac距离中,除了关注考虑了物种的存在与否及其丰度外,还将物种之间的进化关系考虑在内,距离0更侧重于表示两个群落的进化分类完全一致。
例如在16S扩增子测序中,根据16S序列组成构建OTUs进化树,OTUs之间存在进化上的联系,因此不同OTUs之间的(系统发育)距离实际上有“远近”之分。将系统发育树和OTUs丰度数据一起添加至距离的计算中,计算Unifrac距离。而若使用上述提到的其它只基于OTUs丰度数据计算群落距离的方法,则忽略了OTUs之间的进化关系,认为OTUs间的关系平等。当然,并不是说Unifrac距离是最合适16S群落分析的,很多情况下它其实也并没有比只基于OTUs丰度数据计算群落距离的方法(如Bray-curtis距离)“更好”,总之具体问题具体分析吧,根据实际情况选择合适的距离测度。
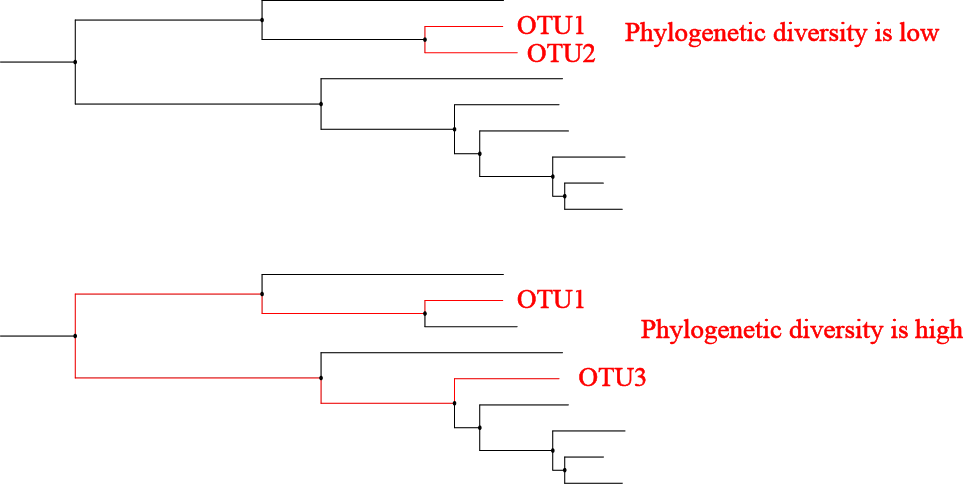
Unifrac距离分为非加权Unifrac距离(Unweighted unifrac distance)和加权Unifrac距离(Weighted unifrac distance)。两种的主要区别是否考虑了物种的丰度。非加权Unifrac距离只考虑了物种有无的变化,不关注物种丰度,若两个微生物群落间存在的物种种类完全一致,则距离为0;加权Unifrac距离同时考虑物种有无和物种丰度的变化,若两个微生物群落间存在的物种种类及丰度完全一致,则距离为0。
对于非加权和加权Unifrac距离的选择,看网上很多帖子给的经验性建议:在环境样本的检测中,由于影响因素复杂,群落间物种的组成差异更为剧烈,因此往往采用非加权方法进行分析。但如果要研究对照与实验处理组之间的关系,例如研究短期青霉素处理后,人肠道的菌落变化情况,由于处理后群落的组成一般不会发生大改变,但群落的丰度可能会发生大变化,因此更适合用加权方法去计算。(来源)
当然这只是建议,实际情况中可能效果并没有那么好,个人体会如此,总之具体问题具体分析吧。
R语言计算相似性指数或距离指数
常见的相似性指数或距离指数,如Jaccard相似性指数、欧几里得距离、Bray-curtis距离等,在R中可通过vegan包vegdist()函数计算。但是需要注意一点,像Jaccard指数这些,本身属性是相似指数,但vegdist()函数的输出结果统统为距离指数,必要时需要通过“S=1-D”转换;本身属性是相异指数的,则无需再作转换。stats包、ade4包、cluster包、FD包等,也提供了计算相似性指数或距离指数的命令,可自行了解。
对于特殊的Unifrac距离,在R中可通过phyloseq包UniFrac()函数计算,GUniFrac包GUniFrac()函数也可以。
相似性或距离的计算中的注意事项
选择合适的度量标准很重要,特别是对于距离测度。例如,在某些情形中我们直接使用了欧几里得距离,但实际上可能不是很合适(特别是在处理物种数据中,欧氏距离因其对称指数的属性,会受到很大的限制)。以相似性或距离为基础的排序或聚类方法强烈依赖于该度量标准的选择。
在计算之前需要确定分析所关注的是Q模式还是R模式(Q模式关注样方间的差异,R模式关注物种间的差异),因为两种模式的适用方法不同(例如Bray-Curtis距离常用于反映各群落间物种组成的差异(Q模式),而不能表示单个物种的分布状态(R模式);同样地,Pearson相关系数对物种之间的关联(R模式)有意义,但不适用于样方之间的关联(Q模式))。
如果主要关注样方之间的差异(Q模式),生态学中的“双零”问题一定不要忽视。
方法选择还取决于数据是定性的(即二元数据,不存在或存在的0-1数据类型)还是定量的(如实际的物种丰度数据)。
关于欧几里得距离应用在群落相似性分析中的常见问题
上面提到了好几次这么一个问题:为什么不建议使用原始物种丰度数据计算欧几里得距离?
欧几里德距离:丰度悖论
上文提到多次,欧几里得距离属于对称指数类型,因此不能有效地处理“双零”问题,而是将“0-0”现象视作“等丰度”对待。当两个样方之间存在很多同为0丰度的物种的情况时,很容易“拉近二者的距离”。
这一点上文有提及,不再额外举例说明了。
另外一方面,欧几里得距离还具有对“物种丰度的差异”比对“物种是否存在”更加敏感的属性。因此,在使用欧几里得距离评估群落相似性时,两个共享很少物种的样方可能看起来比两个共享较多物种但物种的丰度差别很大的样方具有更相似(具有更低的欧几里得距离),干扰我们对群落相似度的判断。对于这种情况,我们举一个例子说明吧。在下面的物种组成矩阵中,样方1和2不共享任何物种,而样方1和3共享所有物种但丰度不同(例如物种3在样方1中的丰度为1,而在样方3中的丰度为8)。然后我们根据欧几里得距离的公式计算群落距离。

根据欧几里得距离,我们得到了这样的结果:样方1和2具有比样方1和3更高的群落相似度!这显然是很难让人接受的,毕竟样方1和2没有共享任何的物种,而样方1和3共享所有物种,仅仅是丰度相差较大而已。对比之下,样方1和3具有比样方1和2更高的群落相似度,这样的结果似乎更容易让人接受。
常见问题示例,“PCA的马蹄形效应”
那么,这种“丰度悖论”会带来怎样的干扰呢?我们举个常见的例子来说明吧。
下图反映了不同环境梯度下物种的丰度分布状态,横轴从左往右,代表了不同的环境梯度,每条曲线代表一种物种,纵轴为物种的丰度。我们知道,自然界的物种大多属于“单峰分布”,即在最适的环境条件下丰度最高;偏离最适环境时,丰度会逐渐降低;当环境差异很大(极端)时,丰度通常就很少了甚至为0。由于每类物种的最适生态位不同,因此各异的环境下各类物种的丰度组成肯定是显著不同的。
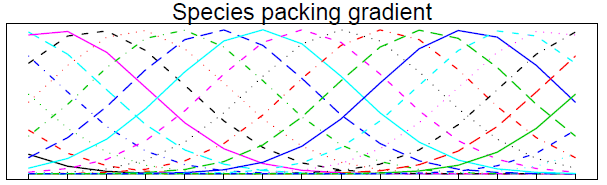
实际的生态学研究中,经常会涉及到在不同环境中的取样调查过程。毫无疑问,当你在一个“较长”的环境梯度内(或者说,在差异很大的几个环境中)取样时,肯定会存在很多物种出现0值的情形。并且两个环境之间差异越大,共享物种就越少。
然后你期望通过排序分析,探究不同环境之间群落差异程度。如果你选择的方法为PCA(PCA以欧几里得距离为基础),并且直接在原始物种丰度(存在非常多的0值,且丰度也通常不均)的基础上执行PCA,那么也就有很大概率出现类似上文提到的情形:具有很多“双零”的样方,距离被“拉近”;很多共享物种数很少的几个样方,比很多共享更多物种数(但共享物种丰度差异较大)的样方,具有“更高的相似性”。最后,PCA排序图呈现出了这么一种状态,形似马蹄,常称为“马蹄形效应”(horseshoe effect)。
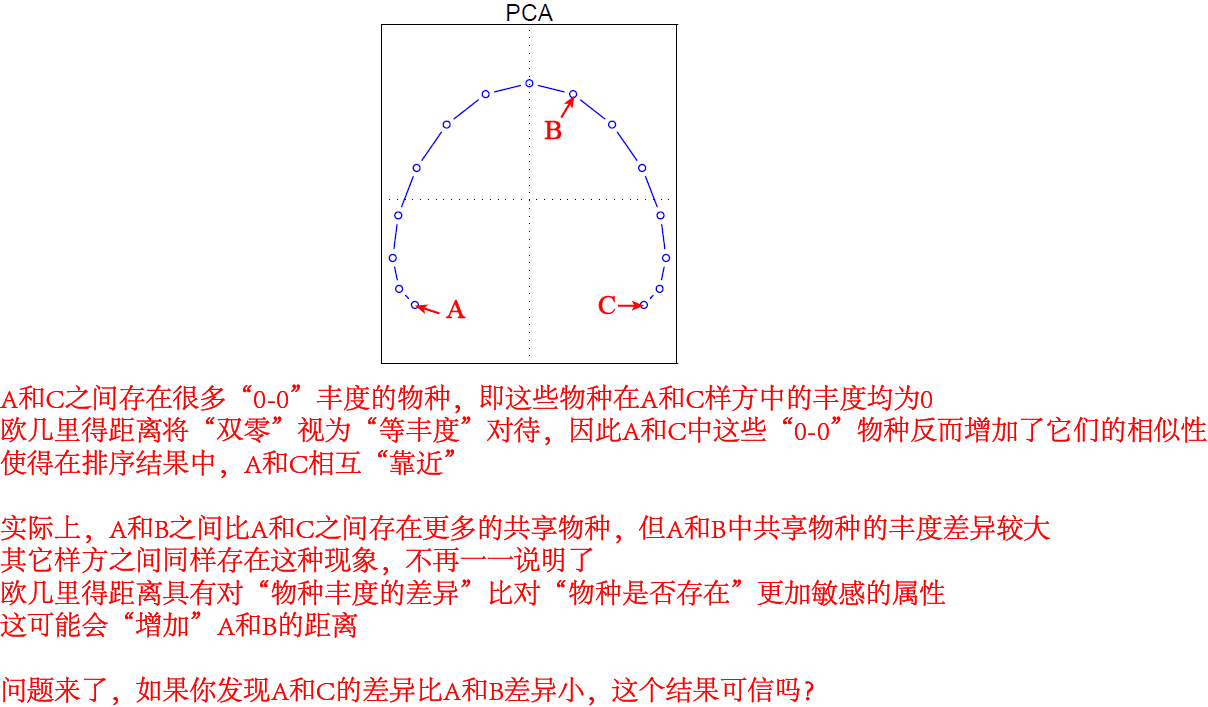
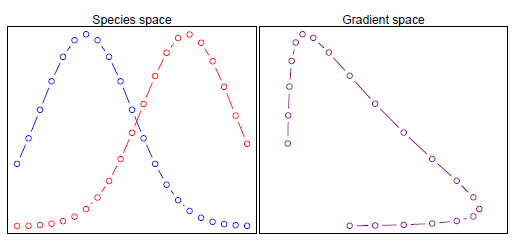
有点懵?来个容易理解的。下图左图每一个点代表一个样方,横轴表示环梯度,纵轴表示物种丰度,这里仅存在两个物种。好了,我们只需要根据这两个物种在各样方中的丰度组成,判断群落相似性即可。当组合两个物种的丰度去执行PCA时,得到了右图的排序结果(产生类似于马蹄形),发现“两极”的环境梯度却具有了较高的群落相似度?实际上,“两极”的环境在两种物种组成上差异是巨大的,因此PCA结果显然是不可靠的。
常用的解决方案
如上文在介绍“欧几里得距离”中提到的那样,在处理物种数据时,一个有效的方法是首先对物种数据执行预转化,如Hellinger转化等,然后再计算欧几里得距离。尽管Hellinger距离仍然是“对称指数”,仍具欧氏距离属性,但它存在“上限2^0.5”(而原始物种数据直接计算得到的欧几里得距离,上限由数据本身决定,有时可以达到很大的值),并且减少了高丰度物种的重要性,降低了欧几里得距离对“物种丰度”的敏感性等,这些有效降低了“双零”问题导致的误差。因此Hellinger距离也通常被认为是处理带有很多零值的生态数据的合适方法之一。这也是为什么在对物种数据执行PCA、RDA时,推荐首先对物种数据执行Hellinger预转化的原因,可有效避免“马蹄形效应”产生。
如果没有硬性要求一定要为欧氏距离属性,那么对于物种数据,最好使用非对称指数计算相异矩阵,例如常见的Bray-curtis距离等。正如上文“对称指数和非对称指数”中所提到的,非对称指数有效解决了“双零”问题。事实上,我们在物种数据的排序分析中也更多地使用PCoA(可以使用任意距离,物种数据中常用Bray-curtis距离等)代替PCA(欧几里得距离属性),原因也是如此了。
参考资料
张金屯. 数量生态学. 科学出版社, 2004.
DanielBorcard, FranoisGillet, PierreLegendre, et al. 数量生态学:R语言的应用(赖江山 译). 高等教育出版社, 2014.
David Zeleny博士:Ecological resemblance
Jari Oksanen1. Multivariate Analysis in Ecology - Lecture Notes -. 2004
Legendre P, Legendre L. Numerical Ecology. Second English edition. Developments in Environmental Modelling, 1998, 20, Elsevier



