纪中游记(十二)
20190818
T0
初
树形DP?果断放弃
复
这道题竟也可以用贪心大法!
按能量大小给每个节点排序,每次找需要能量最小的节点,判断其是否合法(能量能否传输)。如果合法,将答案加一、更新祖先节点的传递能量限制。这样扫一遍就行了。
什么,贪心的证明?不存在的。

1 #include<bits/stdc++.h> 2 using namespace std; 3 int n,ans=0; 4 struct hh 5 { 6 int po,pt; 7 }a[1005]; 8 int wi[1005],fa[1005]; 9 inline int read() 10 { 11 int x=0; 12 char ch=getchar(); 13 while(ch<'0'||ch>'9') 14 { 15 ch=getchar(); 16 } 17 while(ch>='0'&&ch<='9') 18 { 19 x=(x<<1)+(x<<3)+ch-'0'; 20 ch=getchar(); 21 } 22 return x; 23 } 24 bool cmp(hh op,hh ed) 25 { 26 return op.po<ed.po; 27 } 28 int main() 29 { 30 scanf("%d",&n); 31 for(int i=1;i<=n;i++) 32 { 33 fa[i]=read(), 34 a[i].po=read(), 35 wi[i]=read(); 36 a[i].pt=i; 37 } 38 sort(a+1,a+n+1,cmp); 39 for(int i=1;i<=n;i++) 40 { 41 int zu=0; 42 for(int j=a[i].pt;j,zu=j;j=fa[j]) 43 { 44 if(wi[j]<a[i].po) 45 break; 46 47 } 48 if(zu!=0) continue; 49 for(int j=a[i].pt;j;j=fa[j]) 50 { 51 wi[j]-=a[i].po; 52 } 53 ans++; 54 } 55 printf("%d",ans); 56 return 0; 57 }
终
贪心真是越来越重要了
T1
初
想了很长时间,开始想用桶维护,却不会离散化;后来放弃正解转向部分分,却因sort函数被注释爆零(亏了60)
复
看到GMOJ上有一神犇用了十分神奇的方法,什么二分查找通通踩爆!
分析题意可以发现:
答案只和 大于当前区间的区间 与 与当前区间有重合部分的区间 与 当前选择的数值 有关
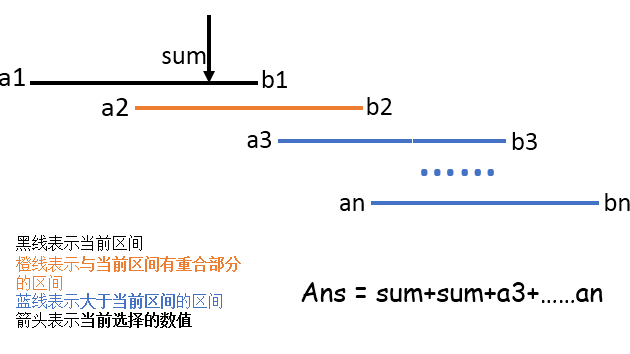
如果区间们不重合,那么答案就只涉及当前选择的数值。再进一步,答案只可能是某个区间的右端点;
如果区间们重合,那么答案还要加上与当前区间有重合部分的区间的值。
这样一来,我们可以将左端点和右端点储存在同一个数组中,再进行排序、预先算出左端点的和为qzh
然后就可以进行以下两种操作:
1.每经过一个左端点,将当前区间的左端点的值从qzh中减去,再维护一个re,表示当前有多少重合的区间;
2.每经过一个右端点,能量就可以用(re*当前选择的数值+qzh)表示,再把re减一。
有了这两种操作,就可以轻松解决这道题了

1 #include<bits/stdc++.h> 2 #define lll long long 3 using namespace std; 4 lll ans=-1,qzh=0; 5 struct hh 6 { 7 lll a;lll b; 8 }aa[200005]; 9 inline long long read() 10 { 11 lll x=0; 12 char ch=getchar(); 13 while(ch<'0'||ch>'9') 14 ch=getchar(); 15 while(ch>='0'&&ch<='9') 16 { 17 x=(x<<1)+(x<<3)+ch-'0'; 18 ch=getchar(); 19 } 20 return x; 21 } 22 bool cmp(hh op,hh ed) 23 { 24 if(op.b==ed.b) return op.a<ed.a; 25 return op.b<ed.b; 26 } 27 int n,oio,re=0; 28 int main() 29 { 30 scanf("%d",&n); 31 for(int i=1;i<=n;i++) 32 { 33 lll jk,kl; 34 jk=read();aa[i].a=1;aa[i+n].a=2; 35 kl=read();aa[i].b=jk;aa[i+n].b=kl; 36 qzh+=jk; 37 } 38 sort(aa+1,aa+1+2*n,cmp); 39 for(int i=1;i<=2*n;i++) 40 { 41 if(aa[i].a==1) 42 { 43 qzh-=aa[i].b; 44 re++; 45 } 46 else 47 { 48 lll num=re*aa[i].b+qzh; 49 if(num>ans) 50 { 51 ans=num; 52 oio=i; 53 } 54 re--; 55 } 56 } 57 cout<<aa[oio].b<<" "; 58 printf("%lld",ans); 59 return 0; 60 }
终
二分查找竟有官方函数?(致远星)
T2
初
Hash?KMP?靠无‘*’情况水得10分
复
在GMOJ上发现了某大佬写的程序,十分详细
果真是我不会的KMP,

1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 int n,m,m1,num,a[101],next[101][200001];//bz[i][j]记录的是第i个区间能否和以 字符串中以j为首的串匹配 8 char s1[101],s2[200001]; 9 bool bz[101][200001]; 10 void kmp(int ar,int lt,int rt)//ar是第几个区间,lt是首端,rt是尾端 11 { 12 if(rt<lt)//如果尾端比首端小 13 { 14 for(int i=0;i<=m1+1;i++) 15 bz[ar][i]=1; 16 return; 17 }//说明根本不需要匹配,全部满组,记录一下跳出函数 18 int len=rt-lt+1,i,j=0,j1=0,p[101];//len是记录一下该区间的长度。 19 p[1]=0;//接下来是标准的KMP算法,P数组在这就是next数组 ,先将p[1]标记位初始值0; 20 //然后先让a字符串进行自我匹配。 21 for(int i1=2;i1<=len;i1++) 22 { 23 i=i1+lt-1; 24 j1=j+lt-1;//由于我们只是取了s1字符串中的一段,真正匹配还是要和原字符串匹配。 25 while(j>0 && s1[j1+1]!=s1[i]) 26 { 27 j=p[j];//如果我想等,就让j到上一个匹配的位置,继续匹配,直到匹配到为止。 28 j1=j+lt-1; 29 } 30 //在这里j1和i的作用都是将当前a区间字符串的位置还原到原数组。 31 if(s1[j1+1]==s1[i]) 32 j++; 33 j1=j+lt-1; 34 p[i1]=j; 35 } 36 j=0; 37 for(int i=1;i<=m1;i++)//匹配的字符是要从1开始的。因为s2[1]这个位置也是要匹配的啊 38 { 39 j1=j+lt-1;//j1用来找到s1数组中的位置 40 while (j>0 && s1[j1+1]!=s2[i]) 41 { 42 j=p[j]; 43 j1=j+lt-1;//随着j值的变化,j1的值也要不断更新 44 } 45 if(s1[j1+1]==s2[i]) 46 j++; 47 j1=j+lt-1;//随着j的值变化而更新 48 if(j==len)//如果j和len的值相等,那就说明匹配成功,将判断数组标记为1, 49 bz[ar][i-j+1]=1;//反之就标记为0,由于初始值为0,所以根本不需要再标记 50 //其中i-j+1表示的就是s2数组中能和a区间匹配的首端,、 51 //因为是在i的位置匹配完的,长度又为len,因此整个是从i-j+1开始匹配成功的。 52 } 53 } 54 bool pd(int st)//st表示是第几个同构串,当然也表示从那一位开始 55 { 56 int i=st,j=1; 57 //j在这里仍然表示的是第几个区间 58 if(bz[j][st]==0) 59 return 0;//如果第一个区间都匹配不成功,那还匹配个鸟啊。直接退出 60 a[0]=0;//还记得a数组吗,a数组表示的是每一个区间的断点 61 while(i!=0 && i+a[j]-a[j-1]-2<=st+m-1)//while这里是啥意思呢,我们仔细理解一下 62 //如果i不等于0,并且i+a[j]-a[j-1]-2小于等于st+m-1就继续循环。 63 //惊奇地发现st+m-1表示的就是长度为m的串的在原来的s2字符串中的最后一位,在这可以理解为位置。 64 //又发现a[j]-a[j-1]-1表示的是字符串中哪个区间的长度,相当于是i+这个长度-1,和上面是一个形式,指的就是这个 65 //区间的长度不能超过同构串的长度,这是最基本的限定 66 { 67 if(j==num-1 && bz[num][st+m-a[num]+a[num-1]+1])//再看,如果j等于num-1;并且第num个区间可以匹配上。 68 //说明匹配成功。这里显然是把最后一个区间单独拿出来讨论了 69 return 1; 70 //而如果匹配失败,i就必须从下一个可能的位置开始匹配。 71 i=next[j][i+a[j]-a[j-1]-2]; 72 //还记得next数组吗 ,next[i][j]数组记录的是bz[i+1][k]==1时,k为大于j的最小值。从这一位开始匹配,不仅快, 73 //而且能保证是正确的 74 j++; 75 } 76 //如果从循环中出来了,说明在循环中,不存在一种情况可以返回1,那就只能返回0了 77 return 0; 78 } 79 int main() 80 { 81 scanf("%s",s1+1); 82 scanf("\n"); 83 scanf("%s",s2+1);//这里是输入部分,将两个字符串输入出来 84 n=strlen(s1+1); 85 m=strlen(s2+1);//找到两个字符串的长度。 86 num=0;//num是一个统计区间个数的变量 87 for(int i=1;i<=m-1;i++) 88 s2[i+m]=s2[i]; //将s2数组有复制一份,满足同构串的性质。这样比较方便找匹配数 89 m1=2*m-1;//复制一份后,m1的长度也当然要复制一份。 90 for(int i=1;i<=n;i++) 91 { 92 if(s1[i]=='*') 93 a[++num]=i; 94 }//这里统计的是每一个区间点,表示在此之前为一个区间 95 a[++num]=n+1;//那为什么要将n+1也设为区间点呢,因为离上一个"*"号之间也隔了一串数,我们也需要记录下来 96 memset(bz,0,sizeof(bz));//将判断数组清零。 97 for(int i=1;i<=num;i++)//进入统计阶段 98 { 99 kmp(i,a[i-1]+1,a[i]-1);//进入匹配函数。这里i表示的是第几个区间,a[i-1]+1是指区间的头,a[i]-1是指区间的尾端。 100 } 101 //弄完了KMP函数,接下来我们要做的就是判定了。 102 for(int i=m1-1;i>=0;i--)//从s2字符串开始逆序统计 103 { 104 for(int j=0;j<=num-1;j++)//j是从0开始到num-1,也就是到所有区间的前一个区间。 105 //j表示的是哪个区间的,由于如果暴力枚举会超时,因此我们再引如一个next数组 106 107 //next[i][j]数组记录的是bz[i+1][k]==1时,k为大于j的最小值,加上这个数组是因为。我们如果想要匹配a的所有区间 108 109 //是一定要按顺序匹配上的,这样记录后不仅能保证按顺序匹配,还能让其尽量小,满足了贪心的策略。 110 //可以证明:对于字符串匹配,我们当然希望越早匹配完越好 111 { 112 next[j][i]=bz[j+1][i+1]?i+1:next[j][i+1];//这句话需要仔细琢磨, 113 }//他的意思是如果bz[j+1][i+1]为1,即从i开始可以匹配那么就为i+1,这样i+1肯定是最小的 114 //而如果bz[j+1][i+1]为0,说明这一位无法匹配那么只能是从next[j][i+1]. 115 //理解一下,这其实是一个动态规划的过程。之前的i从逆序开始枚举到这里就发挥上用场了。 116 //next[j][i+1]肯定在next[j][i+1]之前就已经枚举到答案,如果j+1这一位匹配不到,那也只能最小从i+1为开始匹配, 117 //而从i+1未开始匹配,next[j][i+1]记录的就是从i+1位开始匹配的最大的值了 118 } 119 int ans=0; 120 //ans可以用来统计最终答案 121 for(int i=1;i<=m;i++) //最后一个for循环,这里是在枚举s2中每一个同构串。 122 { 123 if(pd(i))//如果判定正确,说明可以匹配,ans++ 124 //进入最后一个判定函数 125 ans++; 126 } 127 cout<<ans;//输出结果,圆满结束 128 }



