纪中游记(九)
20190813
写在前面的话
哇~前两题是真的简单,后两题是真的难
T0&T1
初&复&终
桶排模板+hash模板
没什么好说的(虽然第一题由于粗心只拿了十分)
T2
初
单点修改当然是树状数组哒,可数据范围让O(n)的单调队列也望尘莫及
没办法,我又不会线段树,只好硬着头皮上O(n*m)
只得了10分,意料之中
复
果不其然,这题正解真是用线段树维护区间最大子段和,
(菜鸡HHHG看着1800多的线段树模板代码瑟瑟发抖)
终
不可能的,太难了,这辈子都不可能码出来的(已疯)
补
2019.08.14.14.50
我完成了(吼吼吼)(感谢MHY大佬的讲解)
果然昨天的线段树模板没有白打
值此兴奋之际,我来讲一下这道题
------------华丽的分割线------------
我们先看题,单点修改再加上查询区间最大子段和
前面的伏笔都指向了一个神奇的数据结构——线段树
而线段树需要维护什么呢?你首先想到的一定是区间最大子段和,没错
那又如何合并呢?看图:
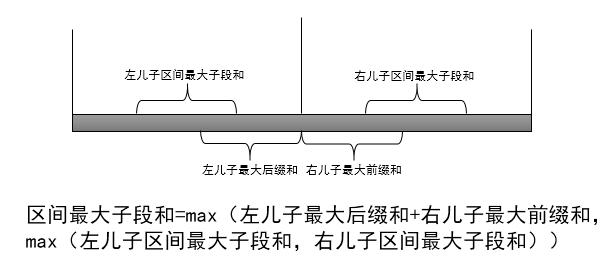
这样就很清晰了,但是题目中是环,所以我们还要维护一个区间最小子段和,最后答案就是:
ans=max(区间总和-区间最小子段和,区间最大子段和)
AC轻(困)轻(难)松(重)松(重)

1 #include<bits/stdc++.h> 2 #define lll long long 3 using namespace std; 4 int n,m; 5 struct oier 6 { 7 lll xl,xr,xm,nl,nr,nm,sum;//最大前缀和,最大后缀和,最大子段和,最小前缀和,最小后缀和,最小子段和,区间和; 8 }lt[400005]; 9 lll a[100005]; 10 inline int ls(int x) 11 { 12 return x<<1; 13 } 14 inline int rs(int x) 15 { 16 return x<<1|1; 17 } 18 void pu(int x) 19 { 20 lt[x].sum=lt[ls(x)].sum+lt[rs(x)].sum; 21 lt[x].xl=max(lt[ls(x)].xl,lt[ls(x)].sum+lt[rs(x)].xl); 22 lt[x].xr=max(lt[rs(x)].xr,lt[rs(x)].sum+lt[ls(x)].xr); 23 lt[x].xm=max(lt[ls(x)].xr+lt[rs(x)].xl,max(lt[ls(x)].xm,lt[rs(x)].xm)); 24 lt[x].nl=min(lt[ls(x)].nl,lt[ls(x)].sum+lt[rs(x)].nl); 25 lt[x].nr=min(lt[rs(x)].nr,lt[rs(x)].sum+lt[ls(x)].nr); 26 lt[x].nm=min(lt[ls(x)].nr+lt[rs(x)].nl,min(lt[ls(x)].nm,lt[rs(x)].nm)); 27 } 28 void build(lll x,lll l,lll r) 29 { 30 if(l==r) 31 { 32 lt[x].sum=lt[x].nl=lt[x].nm=lt[x].nr=lt[x].xl=lt[x].xm=lt[x].xr=a[l]; 33 return ; 34 } 35 lll mid=(l+r)>>1; 36 build(ls(x),l,mid); 37 build(rs(x),mid+1,r); 38 pu(x); 39 } 40 inline void update(lll l,lll r,lll x,lll nn,lll k) 41 { 42 if(l==r&&l==nn) 43 { 44 lt[x].sum=lt[x].nl=lt[x].nm=lt[x].nr=lt[x].xl=lt[x].xm=lt[x].xr=k; 45 return ; 46 } 47 lll mid=(l+r)>>1; 48 if(nn<=mid) update(l,mid,ls(x),nn,k); 49 if(nn>mid) update(mid+1,r,rs(x),nn,k); 50 pu(x); 51 } 52 //oier query(lll xx,lll yy,lll l,lll r,lll x) 53 //{ 54 // oier num={-0x7fffffff,-0x7fffffff,-0x7fffffff,0,0x7fffffff,0x7fffffff,0x7fffffff} ,a={-0x7fffffff,-0x7fffffff,-0x7fffffff,0,0x7fffffff,0x7fffffff,0x7fffffff},b={-0x7fffffff,-0x7fffffff,-0x7fffffff,0,0x7fffffff,0x7fffffff,0x7fffffff}; 55 // //if(l>=xx&&r<=yy) return lt[x]; 56 // lll mid=(l+r)>>1; 57 // if(xx<=mid) a=query(xx,yy,l,mid,ls(x)); 58 // if(yy>mid) b=query(xx,yy,mid+1,r,rs(x)); 59 // num.sum=a.sum+b.sum; 60 // num.xl=max(a.xl,a.sum+b.xl); 61 // num.xr=max(b.xr,b.sum+a.xr); 62 // num.xm=max(a.xr+b.xl,max(a.xm,b.xm)); 63 // num.nl=min(a.nl,a.sum+b.nl); 64 // num.nr=min(b.nr,b.sum+a.nr); 65 // num.nm=min(a.nr+b.nl,min(a.nm,b.nm)); 66 // return num; 67 //}//无用的函数 68 inline lll read() 69 { 70 lll x=0,f=1; 71 char ch=getchar(); 72 while(ch<'0'||ch>'9') 73 { 74 if(ch=='-') 75 f=-1; 76 ch=getchar(); 77 } 78 while(ch>='0'&&ch<='9') 79 { 80 x=(x<<1)+(x<<3)+ch-'0'; 81 ch=getchar(); 82 } 83 return x*f; 84 } 85 int main() 86 { 87 n=read(); 88 for(int i=1;i<=n;i++) 89 { 90 a[i]=read(); 91 } 92 build(1,1,n); 93 m=read(); 94 while(m--) 95 { 96 lll xx,zz; 97 xx=read(),zz=read(); 98 update(1,n,1,xx,zz); 99 //oier ui=query(1,n,1,n,1); 100 printf("%lld\n",max(lt[1].sum-lt[1].nm,lt[1].xm)); 101 } 102 return 0; 103 }
T3
初
直接暴力,成功骗得40分



 浙公网安备 33010602011771号
浙公网安备 33010602011771号