【降维之NMF】NMF(非负矩阵分解)实例
数据介绍:
NMF人脸数据特征提取目标:已知 Olivetti 人脸数据共400个,每个数据是 64*64 大小。
由于NMF分解得到的 W 矩阵相当于从原始矩阵中提取的特征,那么就可以使用NMF对400个人脸数据进行特征提取。
NMF 非负矩阵分解是在矩阵中所有元素均为非负数约束条件下的矩阵分解方法
NMF基本思想:给定一个非负阵V,NMF能找到一个非负矩阵W和一个非负阵H,使得W和H的乘积近似等于V中的值,W:基础图像矩阵(特征)H:系数矩阵
矩阵分解优化目标:最小化W和H的乘积和原始矩阵之间的差别
传统的目标函数(基于欧式距离):
基于KL散度的损失函数:

from numpy.random import RandomState #加载RandomState用于创建随机种子
import matplotlib.pyplot as plt #加载matplotlib用于数据的可视化
from sklearn.datasets import fetch_olivetti_faces #加载Olivetti人脸数据集导入函数
from sklearn import decomposition #加载PCA算法包
n_row, n_col = 2, 3 #设置图像展示时的排列情况
n_components = n_row * n_col #设置提取的特征的数目
image_shape = (64, 64) #设置人脸数据图片的大小
#########################################################################################
dataset = fetch_olivetti_faces(shuffle=True, random_state=RandomState(0))
faces = dataset.data #加载数据,并打乱顺序
# print(faces)
print(len(faces))
print(len(faces[0]))
#########################设置图像的展示方式###############################################
def plot_gallery(title, images, n_col=n_col, n_row=n_row):
plt.figure(figsize=(2. * n_col, 2.26 * n_row)) #创建图片,并指定图片大小(英寸)
plt.suptitle(title, size=16) #设置标题几字号大小
for i, comp in enumerate(images):
plt.subplot(n_row, n_col, i + 1) #选择画制的子图
vmax = max(comp.max(), -comp.min())
plt.imshow(comp.reshape(image_shape), cmap=plt.cm.gray,
interpolation='nearest', vmin=-vmax, vmax=vmax) #对数值归一化,并以灰度图形式显示
plt.xticks(()) #去除子图的坐标轴标签
plt.yticks(()) #去除子图的坐标轴标签
plt.subplots_adjust(0.01, 0.05, 0.99, 0.94, 0.04, 0.) #对子图位置及间隔调整
plot_gallery("First centered Olivetti faces", faces[:n_components])
# print(faces[:n_components].shape) #(6, 4096)
plt.show()
###############################################################################
estimators = [ #对NMF和PCA实例,将他们存于列表中
('Eigenfaces - PCA using randomized SVD',
decomposition.PCA(n_components=6, whiten=True)),
('Non-negative components - NMF',
decomposition.NMF(n_components=6, init='nndsvda', tol=5e-3)) #n_components 指定分解后矩阵的单个维度k init表示W矩阵和H矩阵初始化方式,'nndsvd':非负双奇异值分解 (NNDSVD) 初始化(更适合稀疏性)
]
###############################################################################
for name, estimator in estimators: #分别调用PCA和NMF
print("Extracting the top %d %s..." % (n_components, name))
print(faces.shape) #(400*k) * (k*4096) = (400, 4096) W * H = V
estimator.fit(faces) #调用PCA或NMF提取特征
components_ = estimator.components_ #获取提取的特征
print("components_.shape:",components_.shape)
plot_gallery(name, components_[:n_components]) #按照固定格式进行排列
plt.show() #可视化结果:


本文来自博客园,作者:木子欢儿,转载请注明原文链接:https://www.cnblogs.com/HGNET/p/16843369.html

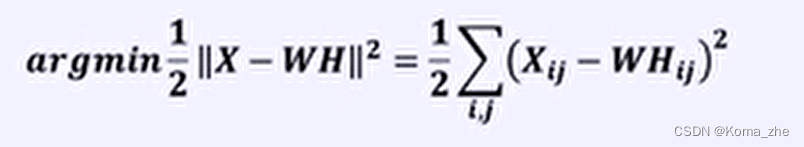
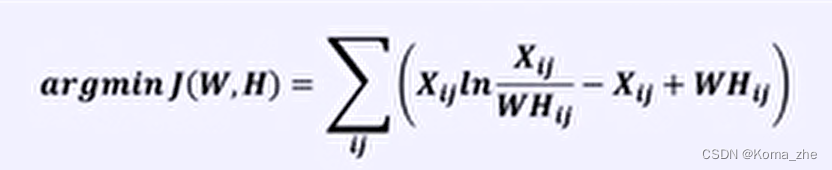

 浙公网安备 33010602011771号
浙公网安备 33010602011771号