【C语言】构建一个校园交通查询系统程序。能够规划出任意出发地和目的地之间的最短路径。
要求
(1)将校园中的重要地点(如教学楼、宿舍楼、餐厅、图书馆等主要地点位置以及主要的道路和路口等联系起来并绘制草图,然后将其抽象为图中的结点(序号)、边,道路中各相邻结点间的近似距离作为边上的权值,形成图结构);
(2)对上述图结构采用邻接矩阵方法进行存储,图中结点的实际名称和图序号之间的对应关系可以另外通过建立一个一维数组对应存储(名称和序号能够实现相互转换);
(3)交通查询:输入一个图中起点位置名称(可由程序转换为结点序号)以及要到达的目的地位置名称(可转换为结点序号),就可通过Floyd算法规划出该两点间的一条最短路径并输出该路径中间所经过的主要位置(结点)的名称序列以及该路径的距离。
代码
#include"stdio.h" #include"stdlib.h" #define MAXVEX 20 #define FINITY 5000 typedef struct { int vexs[MAXVEX]; //顶点类 int arc[MAXVEX][MAXVEX]; //邻接矩阵 int numVertexes; //图中当前的顶点数和边数 int numEdges; } MGraph; typedef int Patharc[MAXVEX][MAXVEX]; typedef int ShortPathTable[MAXVEX][MAXVEX]; void CreateMGraph(MGraph &G) //这个是创建一个图函数 { int i, j, d, k;//d表示权重 printf("学校重点地点有多少和边数:\n"); scanf_s("%d", &G.numVertexes);//顶点 scanf_s("%d", &G.numEdges); //边数 printf("学校名称用序号表示为:\n"); //输入顶点信息,建立顶点节点 for (i = 0; i < G.numVertexes; i++) { scanf_s("%d", &(G.vexs[i])); } //邻接矩阵初始化 for (i = 0; i < G.numVertexes; i++) { for (j = 0; j < G.numVertexes; j++) { G.arc[i][j] = FINITY; } } //这里输入他们的之间的权重 for (k = 0; k < G.numEdges; k++) { printf("输入该建筑与下一个建筑序号以及之间的距离:\n"); scanf_s("%d %d %d", &i, &j, &d); G.arc[i][j] = d; G.arc[j][i] = G.arc[i][j]; } } void print(MGraph *mg) //这是打印第一个邻接表 { printf("初始化的邻接矩阵:\n"); for (int i = 0; i < mg->numVertexes; i++) { for (int j = 0; j < mg->numVertexes; j++) printf("%d\t", mg->arc[i][j]); printf("\n"); } } void Floyd(MGraph G,Patharc *P, ShortPathTable *D) { int v, w, k; for (v = 0; v < G.numVertexes; ++v) { for (w = 0; w < G.numVertexes; ++w) (*D)[v][w] = G.arc[v][w]; (*P)[v][w] = w; } for (k = 0; k < G.numVertexes; ++k) { for (v = 0; k < G.numVertexes; ++v) { for (w = 0; k < G.numVertexes; ++w) { if ((*D)[v][w]>(*D)[v][k] + (*D)[k][w]) { (*D)[v][w] = ((*D)[v][k] + (*D)[k][w]); (*P)[v][w] = (*P)[v][k]; } } } } } int main() { printf("*************************************\n"); printf("*欢迎来到校园交通查询系统*\n"); printf("*************************************\n"); printf("*************************************\n"); printf("*序号分别代表学校内的建筑*\n"); printf("1.宿舍\n"); printf("2.图书馆\n"); printf("3.餐厅\n"); printf("4.教学楼\n"); printf("5.学校中央\n"); printf("**************************************\n"); int v, w, k; MGraph G; Patharc P; ShortPathTable D; CreateMGraph(G); //printf(&G); Floyd(G, &P, &D); printf("各建筑间最短路径如下:\n"); for (v = 0; v < G.numVertexes; ++v) { for (w = v + 1; w<G.numVertexes; w++) { printf("v%d-v%d weight:%d ", v, w, D[v][w]); k = P[v][w]; printf("path: %d", v); while (k != w) { printf("-> %d", k); k = P[k][w]; } printf("-> %d\n", w); } printf("\n"); } printf("最短路径D\n"); for (v = 0; v < G.numVertexes; ++v) { for (w = 0; w < G.numVertexes; ++w) { printf("%d\t", D[v][w]); } printf("\n"); } return 0; }
效果
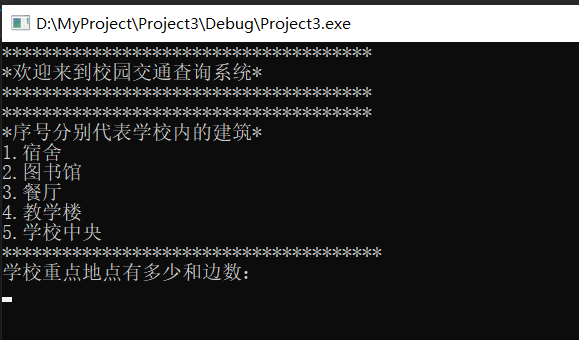
本文来自博客园,作者:木子欢儿,转载请注明原文链接:https://www.cnblogs.com/HGNET/p/14077001.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号