字符串处理

字符串处理

I.KMP

KMP主要应用于字符串匹配问题

KMP相比普通的单模式串匹配的优势在于：对于每次失配，我们不会从头开始，而是从特定的位置开始匹配。

考虑一组样例

模式串 ：abcab
文本串 ：abcacababcab

首先，前四位按位匹配成功，遇到第五位不同。而这时，我们选择将abcab向右移三位，或者可以直接理解为移动到模式串中与失配字符相同的那一位。可以简单地理解为，我们将两个已经遍历过的模式串字符重合，导致我们可以不用一位一位地移动，而是根据相同的字符来实现快速移动。

但有时不光只会有单个字符重复：

模式串：abcabc
文本串：abcabdababcabc

当我们发现在第六位失配时，我们可以将模式串的第一二位移动到第四五位

模式串：   abcabc
文本串：abcabdababcabc

那么现在已经很明了了， KMP 的重头戏就在于用失配数组来确定当某一位失配时，我们可以将前一位跳跃到之前匹配过的某一位。而此处有几个要领：

1.失配数组应建立在模式串上（更灵活嘛）

2.确定位置

首先我们在预处理时应考虑模式串 i 失配时跳转到哪里。因为在文本串中，之前匹配过的所有字符已经没有用了——都是匹配完成或者已经失配的，所以我们的 KMP 数组（即是用于确定失配后变化位置的数组，下同）

在模式串str1 中，对于每一个 str(i) , 他的KMP数组应当是记录一个位置 j , j <= i 并且满足str(i) = str1(j) 并且在 j!=1 时应满足 str(1) 至 str1( j-1 ) 分别于 str(i-j+1) 至str(i-1) 按位相等

代码实现

1、kmp[i] 用于记录当匹配到模式串的第 i 位之后失配,该跳转到模式串的哪个位置，那么对于模式串的第一位和第二位而言，只能回跳到 1，所以当 i=0 或者 i=1 时，相同的前缀只会是 str1(0) 这一个字符，所以 kmp[0]=kmp[1]=1。

如何处理kmp数组呢，我们可以用模式串自己匹配自己

    j=0;//j表示模式串匹配到了第几个字符
    for (int i=2;i<=b.size();i++)//b为模式串
    {
	   while(j != 0 && b[i]! = b[j+1])//此处判断j是否为0的原因在于，如果回跳到第一个字符就不 用再回跳了
       		j=kmp[j];//通过自己匹配自己来得出每一个点的kmp值(回上一个值相同的点)
       if(b[j+1] == b[i])
           j++;
       kmp[i] = j;
        //i+1失配后应该如何跳
	}

就不用写与文本串匹配了吧。

II.字典树（Trie Tree)

字典树常用于统计和排序大量的字符串前缀来减少查询时间

下图就是字典树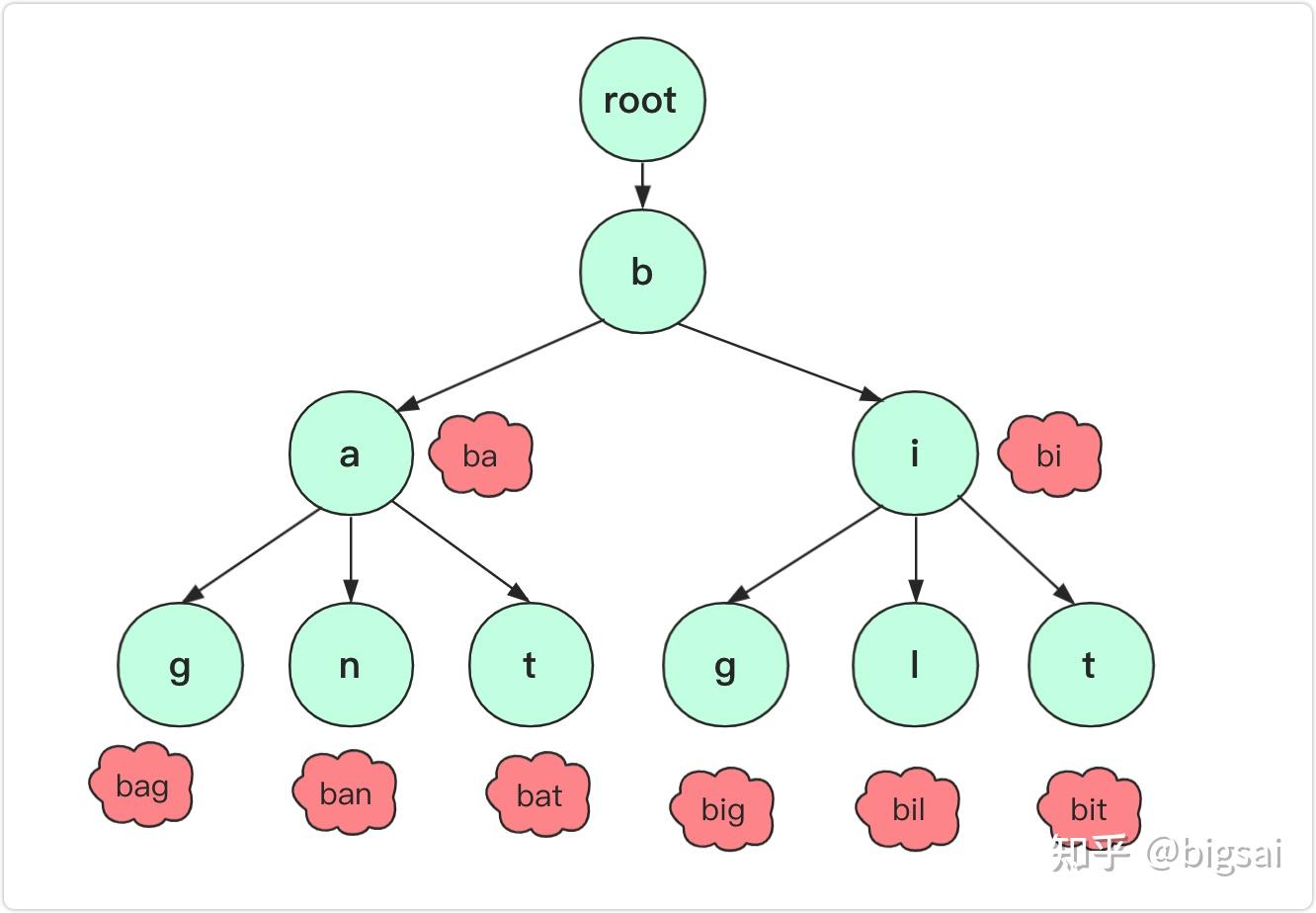

如何搭建字典树呢，太简单了，直接上代码。

struct node{
	int isword;//表示这个节点是不是单词结尾
	int size;//表示这个节点走过多少次
}t[3000005][26];

void build()
{
	int p = 0, len = a.size();
	for(int i = 0; i < len; i++)
	{
		int c = getnum(a[i]);//将字符转化为节点编号（自定义函数）
		if(!t[p][c].size)//没走过
			t[p][c].size = ++idx;
		p = t[p][c].size;
        cnt[p]++;
	}
}

没了。

III.AC自动机

AC自动机就是Trie树和KMP的结合体（在树上KMP）

AC自动机用来解决多模式串匹配，例如给好几个子串，一个母串，让你求子串出现的次数。

搭建AC自动机

通常来讲有两步

1.基础的Trie。

2.KMP思想：对 Trie 树上所有的结点构造失配指针。

字典树构建

按照Trie树的构建方式即可

失配指针

AC自动机利用一个fail指针来辅助匹配。

而fail和KMP中的失配指针有以下区别。

1.共同点：都是在失配时的跳转。

2.不同点，KMP的nxet（即前文的kmp数组）求的是最长 Border（即最长的相同前后缀），而 fail 指针指向所有模式串的前缀中匹配当前状态的最长后缀。

构建指针

构建 fail 指针，可以参考 KMP 中构造 next 指针的思想。

考虑字典树中当前的结点 u，u 的父节点是 p，p 通过字符 c 的边指向 u，即trie(p, c) = u。假设深度小于 u 的所有结点的 fail 指针都已求得。

1. 如果trie(fail(p), c)存在：则让的 fail 指针指向trie(fail(p), c)。相当于在 p 和 fail(p) 后面加一个字符c，分别对应u和fail(u)；
2. 如果trie(fail(p), c)不存在：那么我们继续找到fail(fail(p))。重复判断过程，一直跳 fail 指针直到根结点；
3. 如果依然不存在，就让 fail 指针指向根结点。

如此即完成了fail(u)的构建。

下面将使用若干张 GIF 动图来演示对字符串 i, he, his, she, hers组成的字典树构建 fail 指针的过程：

1. 黄色结点：当前的结点u。
2. 绿色结点：表示已经 BFS 遍历完毕的结点。
3. 橙色的边：fail 指针。
4. 红色的边：当前求出的 fail 指针。

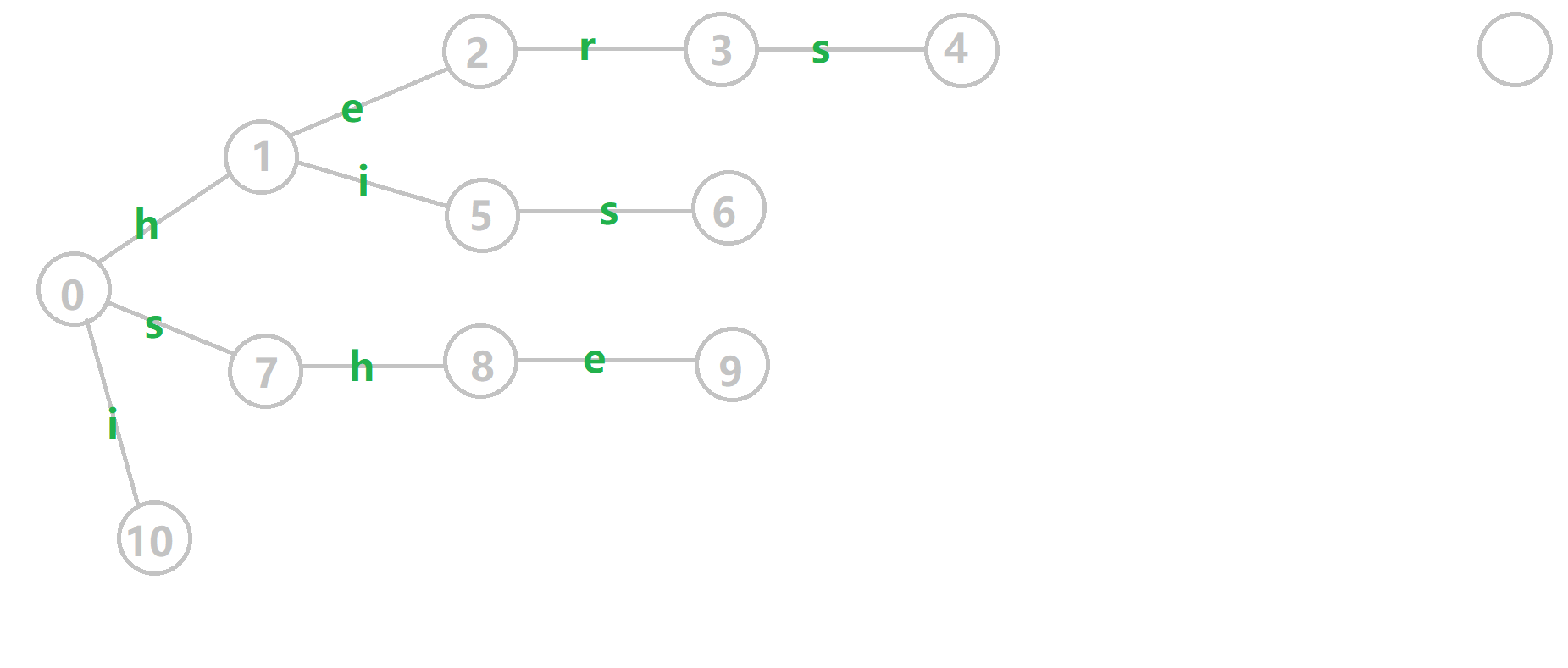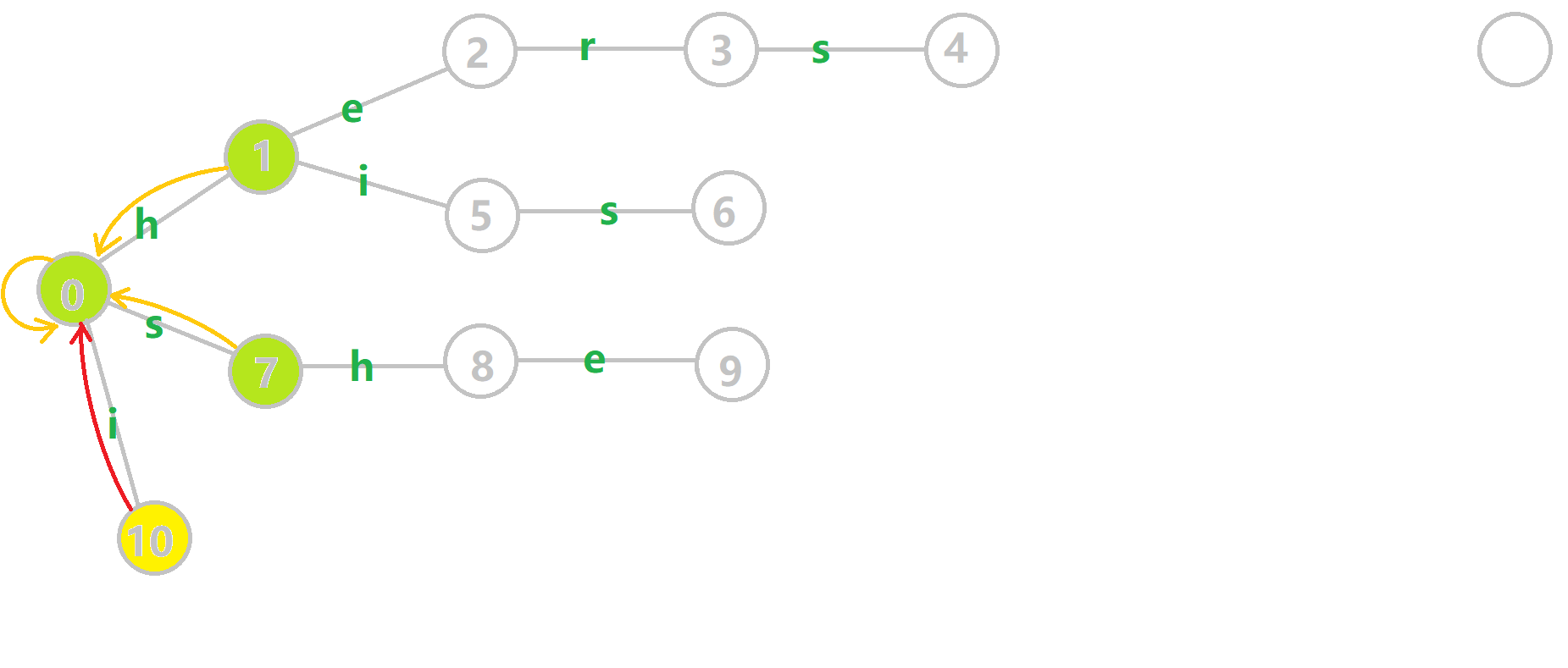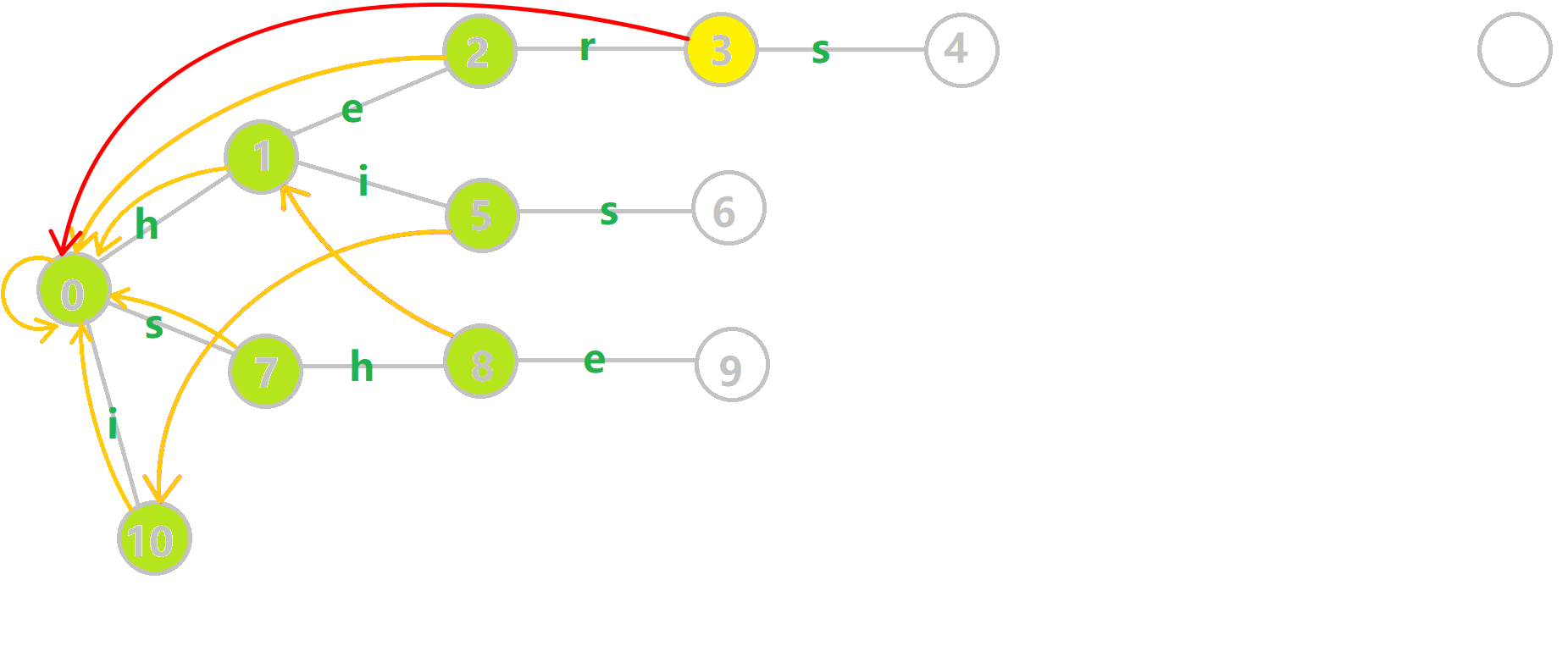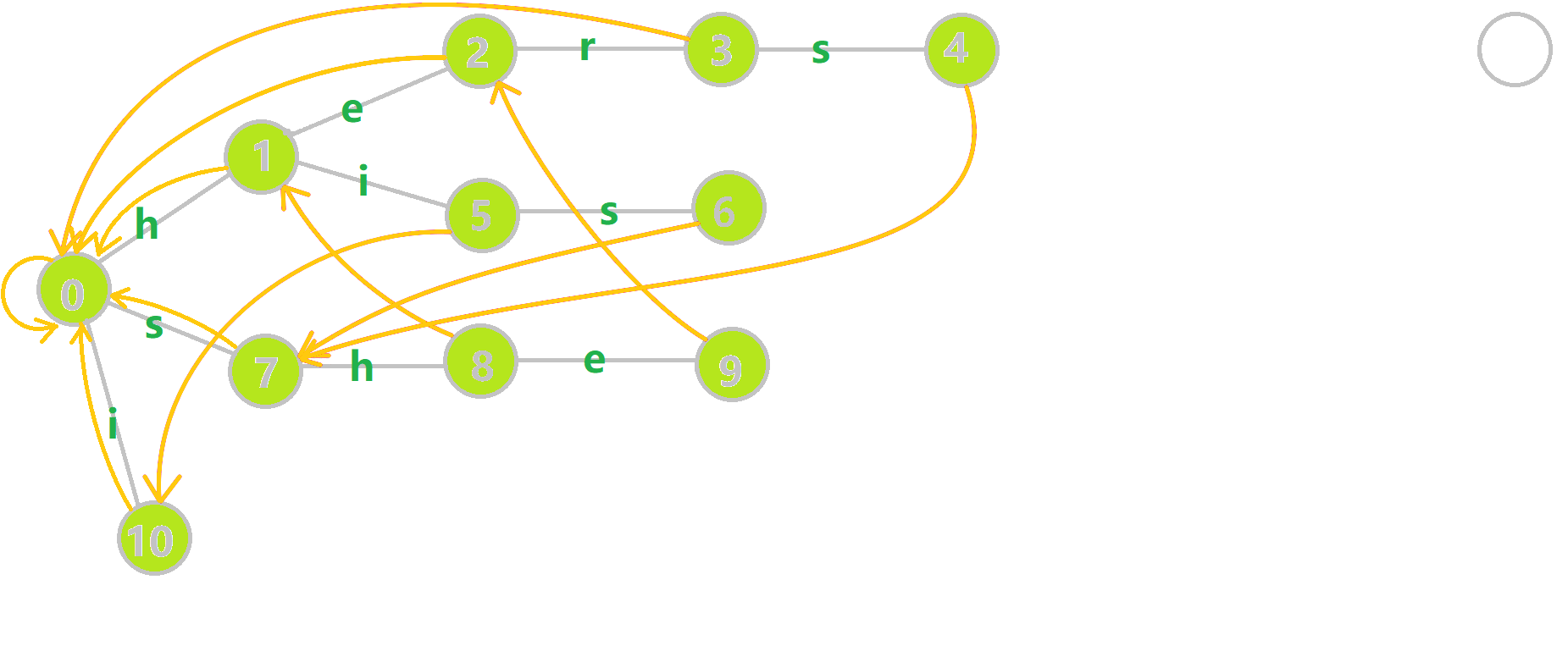
我们重点分析结点6的 fail 指针构建：

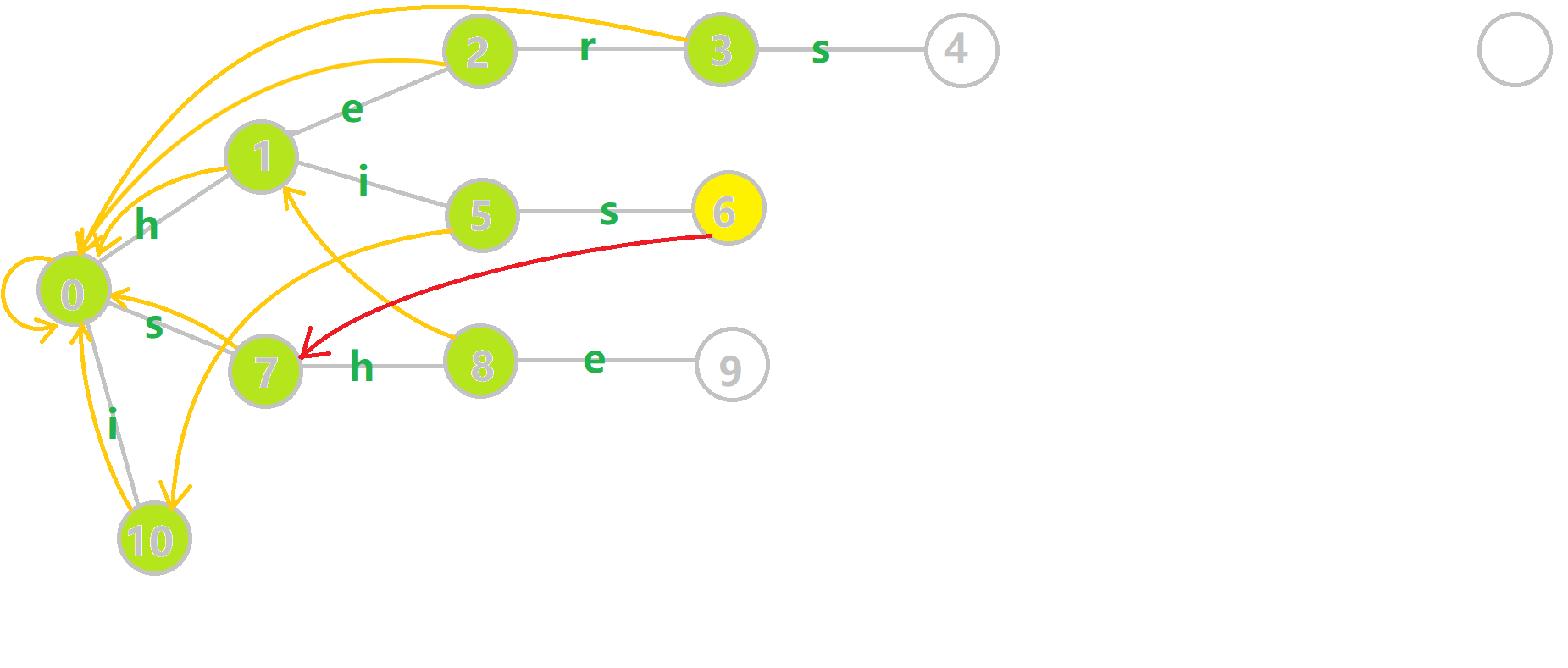
找到6的父结点5，fail(5) = 10。然而结点10没有字母s连出的边；继续跳到10的 fail 指针，fail(10) = 0。发现0结点有字母 连s出的边，指向7结点；所以fail(6) = 7。

代码示例

构造fail指针

（不是本人写的，凑合着看吧）

struct Tree//字典树 
{
     int fail;//失配指针
     int vis[26];//子节点的位置
     int end;//标记以这个节点结尾的单词编号 
}AC[100000];//Trie树
int cnt=0;//Trie的指针 
struct Result
{
      int num;
      int pos;
}Ans[100000];//所有单词的出现次数 
void Get_fail()//构造fail指针
{
        queue<int> Q;//队列 
        for(int i=0;i<26;++i)//第二层的fail指针提前处理一下
        {
               if(AC[0].vis[i]!=0)
               {
                   AC[AC[0].vis[i]].fail=0;//指向根节点
                   Q.push(AC[0].vis[i]);//压入队列 
               }
        }
        while(!Q.empty())//BFS求fail指针 
        {
              int u=Q.front();
              Q.pop();
              for(int i=0;i<26;++i)//枚举所有子节点
              {
                        if(AC[u].vis[i]!=0)//存在这个子节点
                      {
                                AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
                                    //子节点的fail指针指向当前节点的
                                  //fail指针所指向的节点的相同子节点 
                                Q.push(AC[u].vis[i]);//压入队列 
                      }
                      else//不存在这个子节点 
                      AC[u].vis[i]=AC[AC[u].fail].vis[i];
                      //当前节点的这个子节点指向当
                      //前节点fail指针的这个子节点 
              }
        }
}

匹配

int AC_Query(string s)//AC自动机匹配
{
        int l=s.length();
        int now=0,ans=0;
        for(int i=0;i<l;++i)
        {
                now=AC[now].vis[s[i]-'a'];//向下一层
                for(int t=now;t;t=AC[t].fail)//循环求解
                         Ans[AC[t].end].num++;
        }
        return ans;
}

毕