【算法】快速排序
目录结构:
1.简介
排序过程:

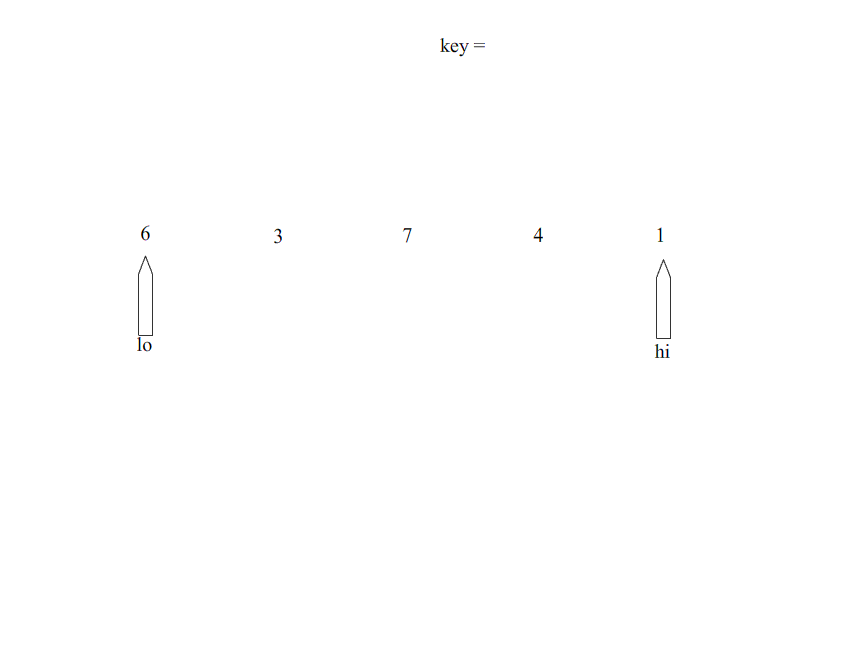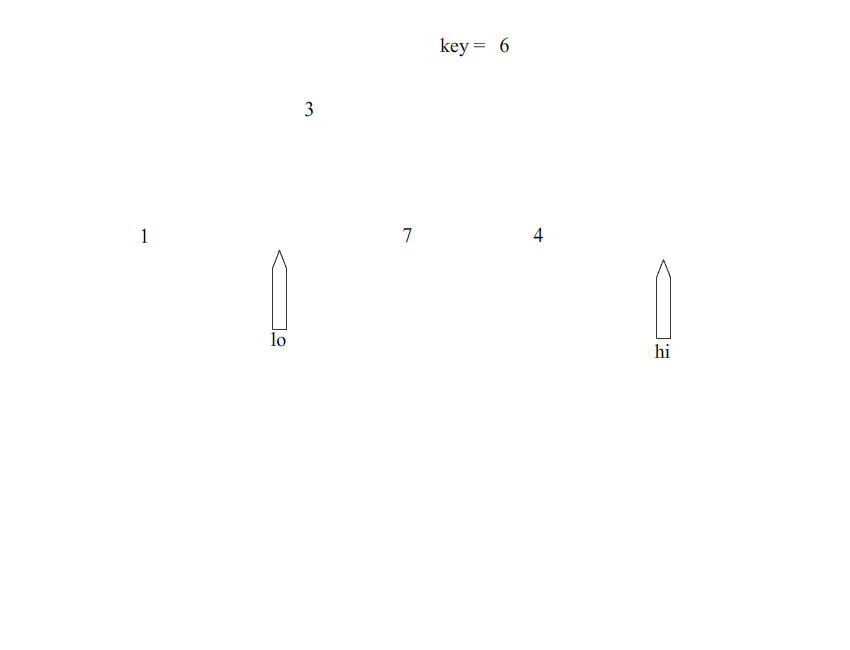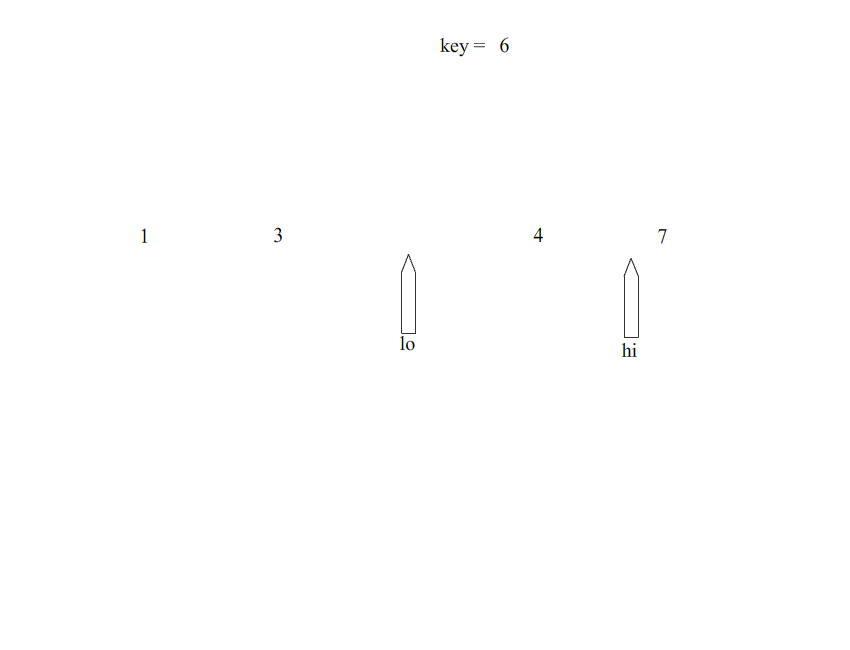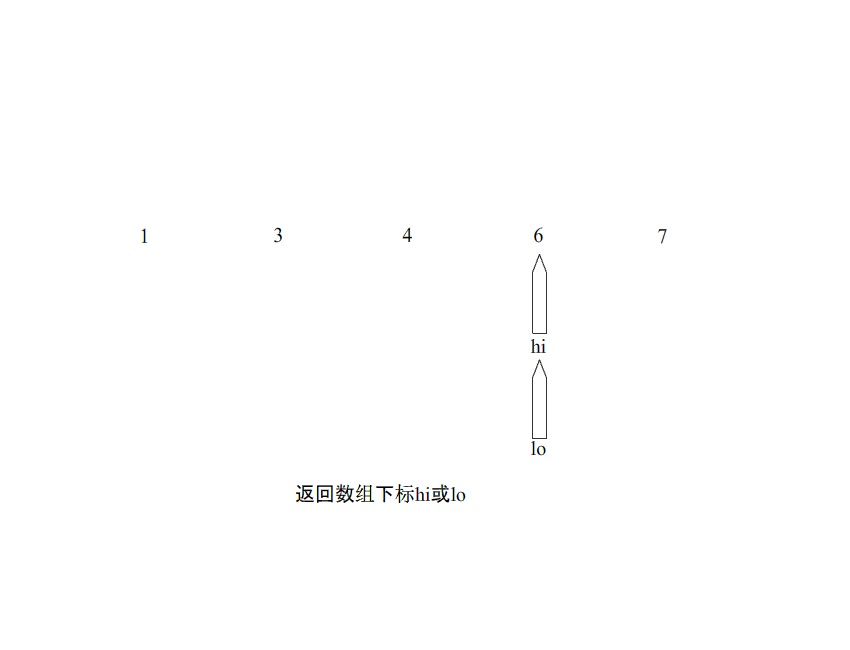
#include <stdio.h> int partition(int* arr,int lo,int hi); void quickSort(int* arr,int lo,int hi); int main() { int arr[]={1,8,2,9,3,7,0,1,0,10}; quickSort(&arr,0,9); for(int i=0;i<10;i++){ printf("%d\n",arr[i]); } return 0; } int partition(int* arr,int lo,int hi){ int key=arr[lo]; //固定切分,选择最左边的点,作为基准点 while(lo<hi){ while(lo<hi && arr[hi]>=key){ //从右边进行遍历 hi--; } arr[lo]=arr[hi]; while(lo<hi && arr[lo]<=key){ //从左边进行遍历 lo++; } arr[hi]=arr[lo]; } arr[lo]=key; return lo; } void quickSort(int* arr,int lo,int hi){ if(lo>=hi){ return; } int index=partition(arr,lo,hi); //得出分界点 quickSort(arr,lo,index-1); quickSort(arr,index+1,hi); }
2.快速排序优化
对于基准位置的选取一般有三种方法:固定切分,随机切分和三数取中切分。三数取中选择基准点,是最理想的一种。
三数取中切分:
int partition(int* arr,int lo,int hi){ //三数取中,使中间数处于lo下标处 int mid=lo+(hi-lo)/2; if(arr[mid]>arr[hi]){ swapArray(arr,mid,hi); } if(arr[lo]>arr[hi]){ swapArray(arr,lo,hi); } if(arr[mid]>arr[lo]){ swapArray(arr,mid,lo); } //调换后的结果,arr[hi]最大,arr[lo]其次,arr[mid]最小 int key=arr[lo]; while(lo<hi){ while(lo<hi && arr[hi]>=key){ hi--; } arr[lo]=arr[hi]; while(lo<hi && arr[lo]<=key){ lo++; } arr[hi]=arr[lo]; } arr[hi]=key; return hi; } //互换数组中两个下标元素的值 void swapArray(int* arr,int a,int b){ int temp=arr[a]; arr[a]=arr[b]; arr[b]=temp; }
3.快排的时间复杂度
在讨论了快排的基本实现之后,接下里继续讨论快排的时间复杂度。快排的平均时间复杂度和最优时间复杂度都是O(n*logn),而最差时间复杂度O(n2)。
在进行讨论快排的最差,最优和平均时间复杂度之前,先来看一下快排的模型图。

一个数列会被分成两个子数列,它们的长度分别是 i - 1 和 n - i , 所以两个子数列的时间就是T(i - 1) 和 T(n - i)。 还有就是分割操作本身也是需要时间的,分割函数 partition 比较简单,只有一个大的循环 while(lo < hi) ,所以这里记一次分割所需的时间为 cn, 其中 c 是一个常数

所以总的时间方程式就是:
T(n) = 左边的时间 + 右边的时间 + 分割所需的时间
= T(i - 1) + T(n - i) + cn
上面的方程式就是一般的时间复杂度方程式,也就是本文后面要讨论的平均时间复杂度的方程式,也是三种方程式(最差,最优,平均)中最难解的。这个方程式的化解,会留到本文的最后。
还有一个特殊的情况,就是当n为0的时候,这时候不需要排序,所以: T(0) = 0. 当n为1的时候,同样也是不需要排序的(只有一个判断 if(lo>=hi) ,消耗的时间为常数), 记:T(1) = T(0) = 0.
因此完整的方程式如下:
|-- 0 (n = 0, or n = 1)
T(n) = |
|-- T(i - 1) + T(n - i) + cn (n > 1)
3.1 最差时间复杂度
接下来我们讨论 最差时间复杂度,在最差的情况下,一个长度为 n 的数列,每次分割得到的两个子数列长度为 n - 1 和 0 。换句话说,就是分割严重不均衡,所有的数据都到一边去了,而另一边没有数据。

两个子序列的长度分别为 n-1 和 0,再加上分割所需的时间,我们可以得出如下的方程式:
T(n) = T(n - 1) + T(0) + cn
因为T(0) = 0,所以
T(n) = T(n - 1) + cn
T(n) = T(n - 1) + C*n T(n - 1) = T(n - 2) + C*(n - 1) # 将 n 减 1,得到下个子序列 T(n - 2) = T(n - 3) + C*(n - 3) .... T(2) = T(1) + C*2 T(1) = T(0) + C

将下一级表达式依次代入上一级,可以得到:
T(n) = T(n - 1) + C*n T(n - 1) = T(n - 2) + C*(n - 1) # 将 n 减 1,得到下个子序列 T(n - 2) = T(n - 3) + C*(n - 3) .... T(2) = T(1) + C*2 T(1) = T(0) + C # 将下一级表达式代入上一级 T(n) = T(0) + C*n + C*(n-1) + C*(n-2) + C*(n-3).....+C*(2)+C # T(0)是等于0的 T(n) = C*n + C*(n-1) + C*(n-2) + C*(n-3).....+C*(2)+C T(n) = C*[n + (n-1) + (n-2) + (n-3).....+2+1]
T(n) = C*(n + 1)*n/2
最后一步,将括号展开,可以得到:
T(n) =C(n2)/2 + C(n/2)
最高阶为 n2, 所以 最差时间复杂度为:O(n2).
时间复杂度为O(n2)绝对是非常糟的(算法的时间复杂度和空间复杂度),那么我们如何避免这种情况出现呢?这里就不得不提上面的基准位置的选取了(第“2.快速排序的优化”)。如果我们选的基准位置是在最左或是最右的位置,而恰好要进行快排的数列是已经按照升序或降序排好了的,那么这个时候,就会出现最糟的情况,所以在这里建议,在选取基准位置的时候,不要选择在最左或是最右的位置,我个人推荐选取到中间(三数取中)。
3.2 最优时间复杂度
上面讨论了最差时间复杂度,接下来继续探讨最优时间复杂度。先来说一下什么是最优的情况,在最优的情况下,每次分割取得的两个子序列的长度相等。换句话说,就是分割非常均匀,每次进行完分割操作(partition)后,分割点以左的长度 恰好等于 分割点以右的长度。

因为每次分割后分割点恰好是在中间(长度为奇数,才可以得到两个分割相等的长度),所以左边消耗的时间为T(n/2), 右边消耗的时间也是T(n/2). 同样,每次分割操作花费的时间依然是cn. 所以我们可以得出如下的表达式:
T(n) = T(n/2) + T(n/2) + cn
= 2T(n/2) + cn
接下就是解递推了:
T(n) = 2T(n/2) + cn # T(n/2) = 2T(n/4) + cn/2
= 2*[2T(n/4) + cn/2] + cn
= 4T(n/4) + 2cn # T(n/4) = 2T(n/8) + cn/4
= 4*[2T(n/8) + cn/4] + 2cn
= 8T(n/8) + 3cn # T(n/8) = 2T(n/16) + cn/8
= 8*[2T(n/16) + cn/8] + 3cn
= 16T(n/16) + 4cn
......
= 2kT(n/2k) + kcn # 一直递推下去,直到 n/2k = 1
= n*T(1) + lgncn # n/2k = 1 ==> 2k = n ==> k = logn
= cn*logn # T(1) = T(0) = 0
最高阶为n logn, 所以 最优时间复杂度为:O(n logn).
3.3 平均时间复杂度
上面说的最优时间复杂度和最差时间复杂度都是比较极端的情况,更多普遍的情况是 平均时间复杂度。有趣的是,在快速排序中,平均时间复杂度等于最优时间复杂度,它们都是 n logn。
因为网页不太好展示解答过程,我已经把推算过程整理成了word文档,下载:排序平均复杂度推算过程。
平均时间复杂度为:O(n logn)
4.空间复杂度
上面已经讨论快排的最优时间复杂度,最差时间复杂度,以及 平均时间复杂度。接下来讨论空间复杂度,就容易多了。 因为每个人实现的算法的具体过程不一样,空间复杂度的情况也比较多。这里笔者只讨论上面的案例代码的空间复杂度,上面算法案例是比较普遍的实现过程,其中的分割(partition)也被称为 in-place partition.
4.1 最优空间复杂度
在平均情况下,一个数列是会被左右等分的。通过观察partition函数,我们可以知道 partition 分配的额外变量是一个常数,也就是说不会随着n的规模(lo 到 hi 的个数)的改变而改变。

上面只分配了一个额外的变量key( 这里不考虑参数),其实即使算上参数消耗,消耗的空间也是固定的(因为参数中的变量大小和输入数组的规模几乎无关系),因此Partition所需要的额外空间是O(1).
到这里我们知道了,快排的空间消耗几乎都来自于栈递归,因此我们只需要知道递归栈的深度就可以了。
总的空间复杂度 = 每次压栈所需的空间 * 总的递归栈的深度
总的递归深度,每一次在平均情况下,所有的数列都会被分为相等的两部分(n/2)。这里假设栈的深度为K,也就是在深度为K时,当前数列的长度为1。 可以得到下面的式子:
n (1 / 2)k = 1
k = log2n
因此,总的空间复杂度就是:
总的空间复杂度 = 每次压栈所需的空间 * 总的递归栈的深度
= O(1) * O(log2n)
= O(logn)
因此,最优空间复杂度就是O(logn)
4.2 最差空间复杂度
上面讨论过了最优空间复杂度,接下来继续分析最差空间复杂度。最糟糕的情况,就是所有的数全分到一边去了,而另一边完全没有数据。这种情况下,时间复杂度为O(n2)。这里我们来继续分析它的最差空间复杂度。
最差的情况下,程序递归的深度就是O(n),递归的次数就等于递归的深度, 而每次递归分配的空间是恒定的,所以我们可以得出:
最差空间复杂度 = 单次所需要的空间 * 递归的深度
= O(1) * O(n)
= O(n)
因此,最差空间复杂度就是O(n).
4.3 平均空间复杂度
其实,在平均情况下,递归的次数为logn。可以这样来理解,因为平均时间复杂度是nlogn,而且每次partition消耗的时间的几乎就是n, 所以可以得出递归的次数就是logn。
由于递归的深度是不确定的,因为它既有可能是二均分,也有可能是所有元素都分到一边去了,也有可能是其他的情况。所以这里可以将递归次数理解为递归深度,都是logn。
平均空间复杂度 = 单次所需要的空间 * 递归的深度
= O(1) * O(logn)
= O(logn)
因此,平均空间复杂度就是O(logn).



 浙公网安备 33010602011771号
浙公网安备 33010602011771号