计算机图形学：凹凸贴图、法线贴图、切线空间、TBN矩阵

凹凸映射

凹凸映射（bump mapping）是一种常见的纹理应用。凹凸映射通过“扰动”（perturb）模型表面的法线方向来改变光照结果，从而为模型提供更多细节，但并不会真正改变模型的顶点位置，因此一般在Fragment Shader中进行。若将一个高精度的法线信息套用在低精度模型上，可以增加低精度模型的渲染细节。

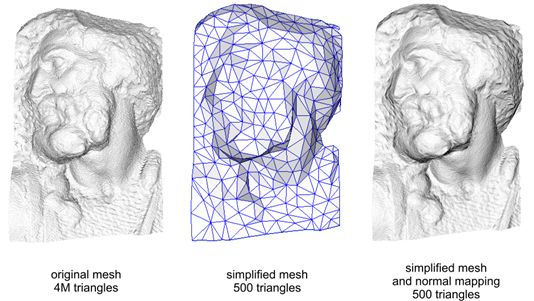
如何实现凹凸映射，也就是如何保存法线信息到纹理上，如何从纹理上获得法线信息。需要解决的问题有两个：

  1. 方向是相对于坐标空间来说的。涉及到方向信息，那必然涉及到方向定义在哪个坐标空间中，涉及到坐标系转换。
  2. 一般纹理存储的是代表颜色值的三维/四维向量，保存的法线信息和颜色值应该通过什么样的计算/映射相互转化。

对于第二个问题，主要实现方法有两种：一种方法是使用凹凸贴图（bump map）存储一系列相对于表面的高度信息，再通过计算得到法线信息；另一种方法是使用法线贴图（normal map）来直接存储表面法线，经过简单映射即可从颜色信息转换为法线信息。

凹凸贴图

凹凸贴图（bump map）相较于普通的纹理，其存储的不是颜色值，一般是使用一张灰度图来存储一系列模型顶点相对于表面的高度信息，并以该高度信息来“扰动”表面法线方向，因此也叫高度贴图（height map）。灰度值越小表示该位置的表面相对于原表面越向外凸起，灰度值越大表示该位置的表面相对于原表面越向内凹陷。但时刻记住，凹凸映射是通过改变表面法线方向来改变光照结果，表面几何信息没有任何变化。

我们可以从凹凸贴图中明确知道一个模型表面的凹凸情况，但使用凹凸贴图的缺点是计算更加复杂，在实时计算时不能直接得到表面法线，而是需要根据纹理UV坐标采样到的灰度值以及邻近的灰度值通过差分法（有限差分近似导数）先得到切线，再计算获得法线。具体计算方法如下：

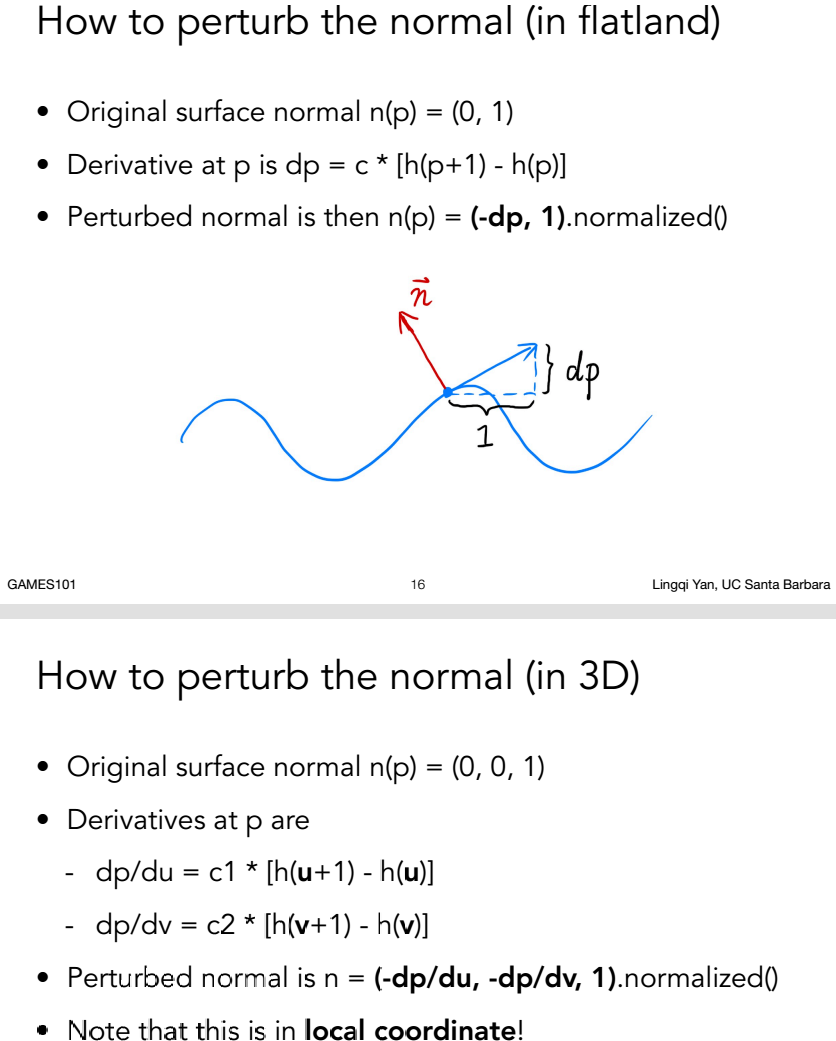
注意：计算得到的结果位于局部坐标系中，若法线信息存储在模型顶点的切线空间中，则得到的法线为切线空间中的法线方向，要想将这个法线方向应用到光照中还需要经过坐标转换，TBN矩阵就是用来做这一转换的。

法线贴图

法线贴图直接存储表面法线方向，相较于凹凸贴图，从法线贴图上采样颜色值到获取法线方向只需要一个简单映射。由于法线方向的分量范围在\([-1,1]\)，而纹理颜色值分量范围为\([0,1]\)，因此映射如下：

\[pixel = \frac{normal+1}{2} \\ normal = pixel \times2-1 \]

那么回到最开始提到的第一个问题，法线贴图中存储的法线在哪个坐标空间中？比较直接的想法就是像表面法线一样，把修改后的模型空间中的表面法线经过上述映射存储在一张纹理中，这种纹理被称为是模型空间（object-space）的法线贴图。由于存储在模型空间中，法线方向可能向各个方向散开，映射到颜色值上使法线贴图看起来效果是五颜六色的，如法线方向（0,1,0）映射到颜色值上对应RGB（0.5,1,0.5）为浅绿色。因此模型空间下的法线贴图看起来如下图：

然而存储在模型空间中的法线信息是绝对法线信息，当我们尝试将这样的法线信息应用于UV动画或其它模型上时就会出错。因此在实际中我们常常会存储在另一种坐标空间，即模型顶点的切线空间中，这样存储的纹理被称为是切线空间（tangent-space）的法线贴图。

切线空间的法线贴图存储的是相对法线信息，即各个点在各自切线空间中的法线扰动方向，切线空间的z轴方向由顶点法线方向定义，因此若顶点法线没有扰动，则存储的相对法线信息为（0,0,1），映射到颜色值上对应（0.5,0.5,1）浅蓝色。顶点法线一般不会被大幅度扰动，因此扰动后的法线方向总是靠近z轴方向，法线贴图总是如下图一样呈现大片蓝紫色：

而且由于存储的是切线空间下的相对法线信息，这样的信息应用于UV动画或其它模型上也不会出错。

切线空间与TBN矩阵

任何坐标空间都由三个互相正交的基向量构成，切线空间也是同理。切线空间由三个互相正交的基向量t,b,n组成。首先，切线空间定义在模型的每一个顶点上，切线空间的原点就是顶点本身，z轴是顶点的法线方向，也称为n轴（normal）；x轴是顶点的切线方向，也称为t轴（tangent）；y轴由法线和切线叉乘得到，也叫副切线，称为b轴（bitangent）。如下图：

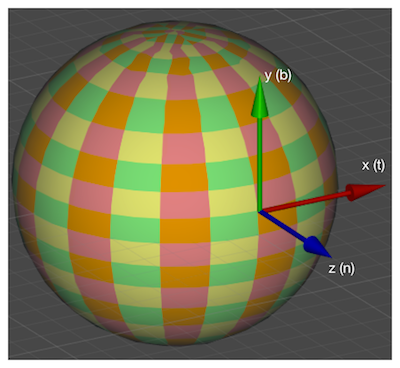
n轴可由顶点法线直接确定，而切线有无数条，如何确定t轴和b轴方向呢？法线贴图的切线T与副切线B定义一般与纹理坐标的U,V对齐，因此也利用这个特性来确定每个表面顶点切线空间的t,b轴方向。

首先取当前顶点所在三角面的三个顶点\(P_1,P_2,P_3\)的模型空间坐标与对应的UV坐标，如图：

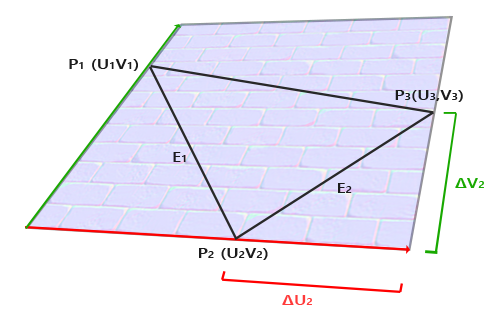
为了建立与u,v轴对齐的t,b轴，计算三角面三个顶点在纹理坐标上的差值\(\Delta U_1,\Delta U_2\)，我们可以建立如下关于切线向量\(T\)和副切线向量\(B\)的线性组合：

\[P_2-P_1=\Delta {U_1}T+ \Delta {V_1}B \\ P_3-P_2=\Delta {U_2}T+ \Delta {V_2}B \]

将向量展开，并将两条边的表示写作\(E_1,E_2\)：

\[(E_{1x},E_{1y},E_{1z})=\Delta{U_1}(T_x,T_y,T_z)+ \Delta{V_1}(B_x,B_y,B_z) \\ (E_{2x},E_{2y},E_{2z})=\Delta{U_2}(T_x,T_y,T_z)+ \Delta{V_2}(B_x,B_y,B_z) \]

写成矩阵形式：

\[\begin{bmatrix} E_{1x}&E_{1y}&E_{1z} \\ E_{2x}&E_{2y}&E_{2z}\end{bmatrix}= \begin{bmatrix} \Delta{U_1} & \Delta{V_1} \\ \Delta{U_2} & \Delta{V_2} \end{bmatrix} \begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z\end{bmatrix} \]

两边同乘逆矩阵将差值部分左移，得到关于\(T,B\)的等式：

\[\begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z\end{bmatrix} = \begin{bmatrix} \Delta{U_1} & \Delta{V_1} \\ \Delta{U_2} & \Delta{V_2} \end{bmatrix}^{-1} \begin{bmatrix} E_{1x}&E_{1y}&E_{1z} \\ E_{2x}&E_{2y}&E_{2z}\end{bmatrix} \]

使用伴随矩阵法求解逆矩阵：\(A^{-1}=\frac{A^*}{det(A)}\)，最终得到如下等式：

\[\begin{bmatrix} T_x & T_y & T_z \\ B_x & B_y & B_z\end{bmatrix} = \frac{1}{\Delta{U_1}\Delta{V_2}-\Delta{U_2}\Delta{V_1}} \begin{bmatrix} \Delta{V_2} & -\Delta{U_1} \\ -\Delta{U_2} & \Delta{U_1} \end{bmatrix} \begin{bmatrix} E_{1x}&E_{1y}&E_{1z} \\ E_{2x}&E_{2y}&E_{2z}\end{bmatrix} \]

至此，我们可以根据三角形三个顶点和UV坐标来得到对齐u,v轴的t,b轴方向了，实际中只需根据公式求出\(T\)，再由\(N\)和\(T\)叉乘得到\(B\)。

建立起切线空间后，根据基向量变换，不难得到从模型空间向切线空间转换的话只需左乘如下矩阵（其中\(N\)为顶点法线向量）：

\[\begin{bmatrix}x_{tangent} \\ y_{tangent} \\ z_{tangent}\end{bmatrix}= \begin{bmatrix}T_x & T_y & T_z \\ B_x & B_y & B_z \\ N_x & N_y & N_z\end{bmatrix} \begin{bmatrix}x_{object} \\ y_{object} \\ z_{object}\end{bmatrix} \]

那么将凹凸贴图或法线贴图上的法线信息从切线空间向模型空间转换的话，只需左乘该矩阵的逆矩阵后作归一化。已知该矩阵定义了一个正交的坐标空间，那么该矩阵为正交矩阵，正交矩阵的逆等于转置，这就得到了TBN矩阵：

\[\begin{bmatrix}x_{object} \\ y_{object} \\ z_{object}\end{bmatrix}= \begin{bmatrix}T_x & B_x & N_x \\ T_y & B_y & N_y \\ T_z & B_z & N_z\end{bmatrix} \begin{bmatrix}x_{tangent} \\ y_{tangent} \\ z_{tangent}\end{bmatrix} \]

补充

应用上述方法虽然t轴和b轴可以与纹理坐标u轴v轴对齐，但uv不一定是相互垂直的，这就使得求得的\(T\)不一定正确，有时候在求得\(T\)后还需要做一步操作——施密特正交化：

\[T_⊥=normalize(T-(T \cdot N)N) \\ B_⊥=normalize(B-(B \cdot N)N - (B \cdot T_⊥)T_⊥) \]

施密特正交化的几何意义就是将“任意坐标系”转换成“直角坐标系”。\(N\)已知，求得\(T\)后对其进行施密特正交化，再叉乘得到\(B\)，即可构造出正确的切线空间。

参考

posted @ 2021-09-25 22:17  HighDefinition  阅读(2244)  评论(0)  编辑  收藏  举报