3D数学：欧拉角、万向锁、四元数

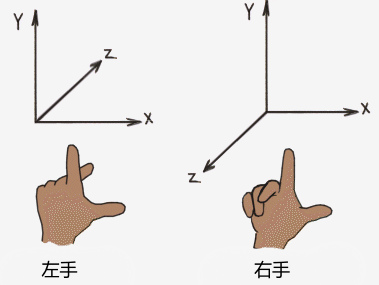
左手系、右手系

欧拉角

欧拉角用来在3D世界中表示物体的朝向，通常我们将朝向定义为将某一个正朝向旋转至当前朝向所进行的变换。当我们表示物体的朝向时，实际上指的是对物体所进行的旋转变换。

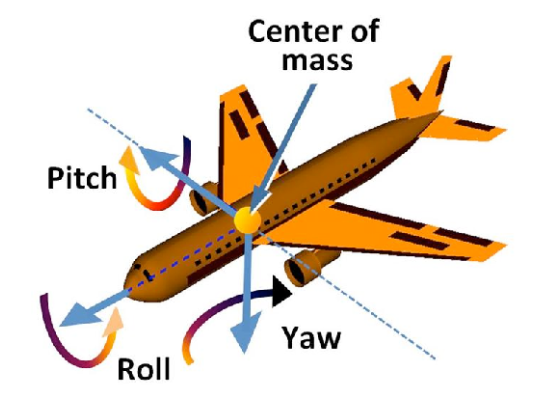
3D世界中的任何一个旋转都可以拆分为沿着物体自身的三个正交坐标轴的旋转，而欧拉角规定了这三次旋转的角度，根据绕轴不同我们分别称它们为偏航角yaw（绕X轴）、俯仰角pitch（绕Y轴）和翻滚角roll（绕Z轴），下图是一个右手系的yaw-pitch-roll表示图：

对于一个旋转变换，我们可以将其用如下三个旋转矩阵相乘的形式表示：

\[E(yaw,pitch,roll)=R_z(yaw)R_y(roll)R_x(pitch) \]

\(R_z\)、\(R_y\)、\(R_x\)分别是绕Z轴、绕Y轴、绕X轴旋转的旋转矩阵：

\[R_z(\theta) = \begin{pmatrix} cos\theta & -sin\theta & 0 & 0 \\ sin\theta& cos\theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

\[R_y(\theta) = \begin{pmatrix} cos\theta & 0 & sin\theta & 0 \\ 0 & 1 & 0 & 0 \\ -sin\theta& 0 & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

\[R_x(\theta) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & cos\theta & -sin\theta & 0 \\ 0 & sin\theta & cos\theta & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \]

由于矩阵乘法的本质是将左侧矩阵表示的变换信息应用于右运算元（向量/矩阵），而多个线性变换间一般是不可交换的，即矩阵乘法不满足交换律。所以三次旋转的顺序非常重要，在Unity、UE4、3dsMax等软件中，以欧拉角形式调整旋转时一般会将旋转顺序固定，而这正是导致万向锁（Gimbol Lock）即万向节死锁的原因。

万向锁

网上很多资料的说法都是绕固定旋转顺序的中间轴旋转90°后使得哪两个轴重合或哪两个万向节共面了从而丢失一个维度上的自由度，或者以一个使用万向节的陀螺仪模型来进行演示，这就让人很摸不着头脑。在最初的设想里物体总是以自身物体坐标系为参照进行旋转，怎么可能使得哪两个轴重合；而陀螺仪虽然演示清楚了，但为什么在Unity等软件和3D数学上会出现万向锁问题，感觉在本质问题上还是没有说明清楚。

Unity中的万向锁问题

在Unity3D中固定使用Z->X->Y这套旋转顺序，即\(E(yaw,pitch,roll)=R_y(yaw)R_x(roll)R_z(pitch)\)，每一次乘上旋转矩阵，即进行一次旋转变换，我们认为就有一个万向节Gimbal来控制这个变换过程。无论给定旋转如何，都以这个固定的旋转顺序来处理。

在Unity3D Scene视图中进行旋转操作时，红色圈为X旋转轴，绿色圈为Y旋转轴，蓝色圈为Z旋转轴，这些圈即Gimbal。

首先说明一下几个坐标系的概念：

• 世界坐标系：表示物体相对于世界原点的绝对坐标。
• 物体坐标系：表示物体相对于父物体的相对坐标。
• 惯性坐标系：与物体位于同一位置，但轴向平行于世界坐标系的坐标系。

由于使用欧拉角更直观，在Unity Inspector上使用欧拉角表示旋转，而在底层使用四元数表示旋转以避免万向锁问题。Unity使用左手Y-up坐标系，因此Inspector上用欧拉角表示时X轴、Z轴旋转是绕当前物体的局部坐标系的X轴、Z轴进行旋转，而Y轴旋转是绕当前物体的惯性坐标系的Y轴进行旋转，这正是造成万向锁问题在Unity中理解不直观的原因：Inspector上的Y轴旋转并不是绕物体坐标系旋转！

Inspector Y轴默认绕惯性坐标系旋转

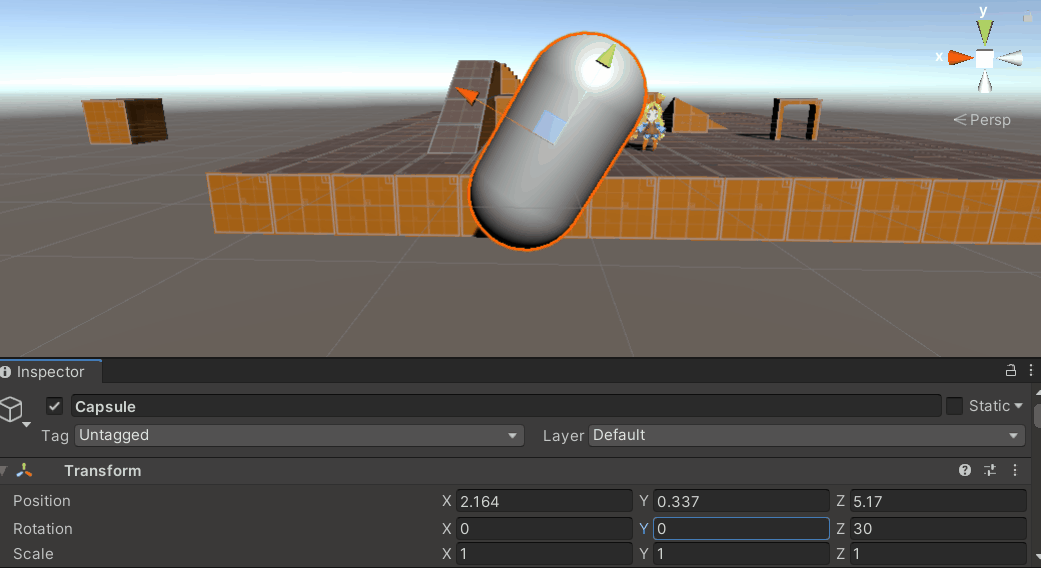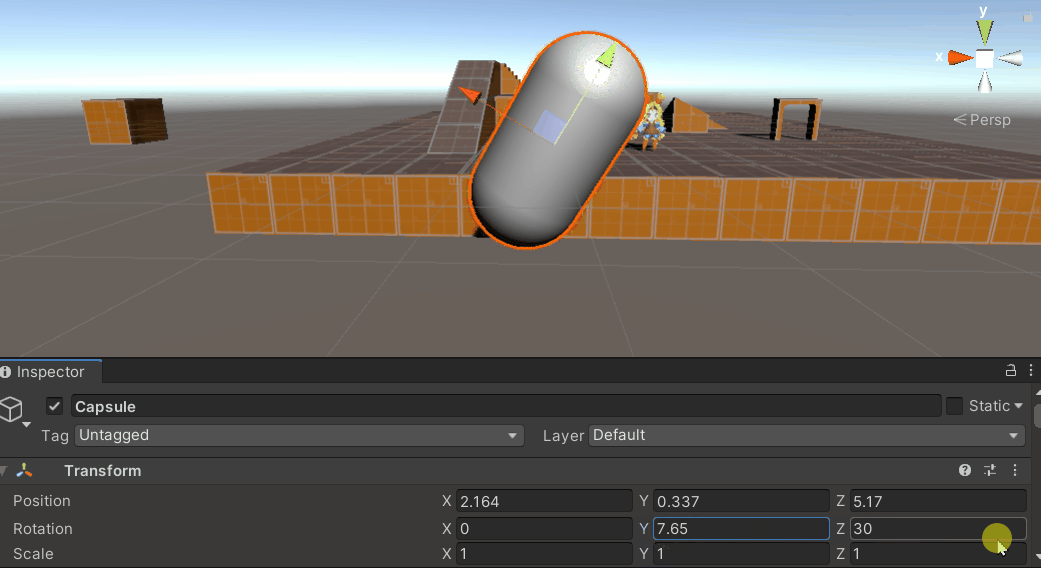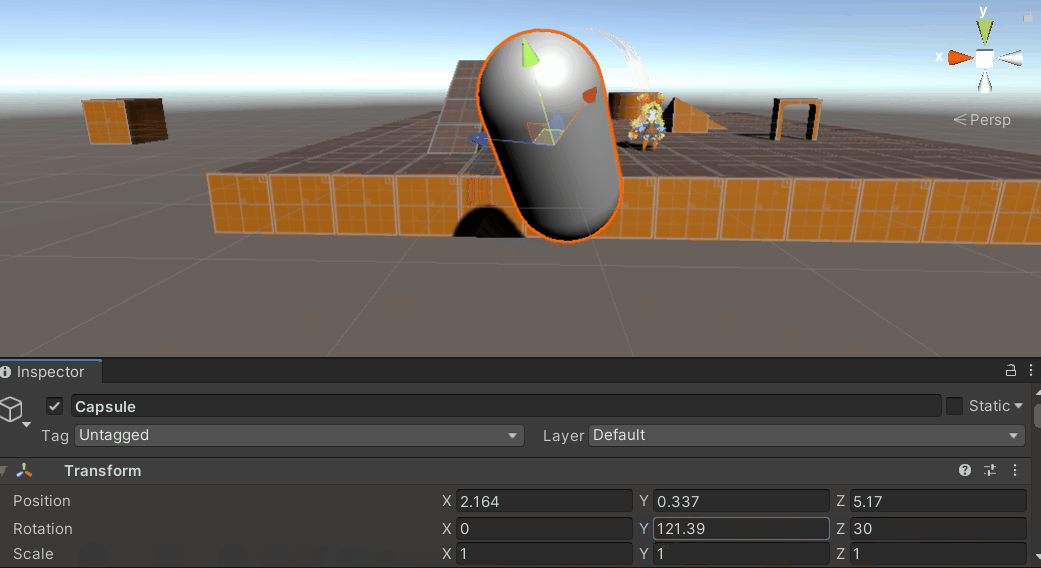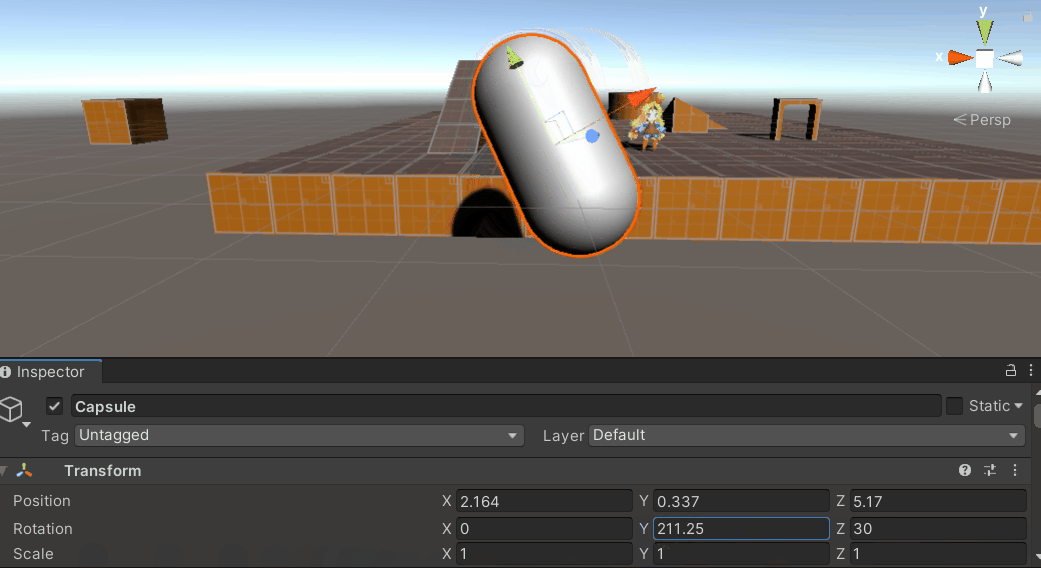
在网上大多数资料中，Unity中的万向锁问题被表述为，当物体绕中间轴X轴转动到达90°或-90°附近时，此时物体坐标系下的Z轴与惯性坐标系下的Y轴负向或正向重合，导致此时Y轴和Z轴旋转等价，物体的旋转丢失了一个维度上的自由度。

Unity中的万向锁问题

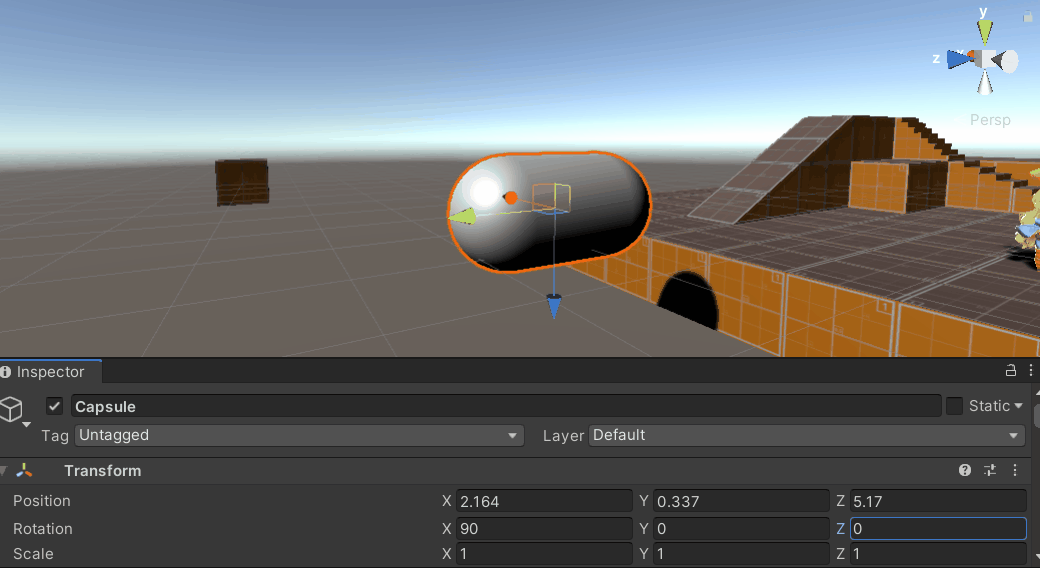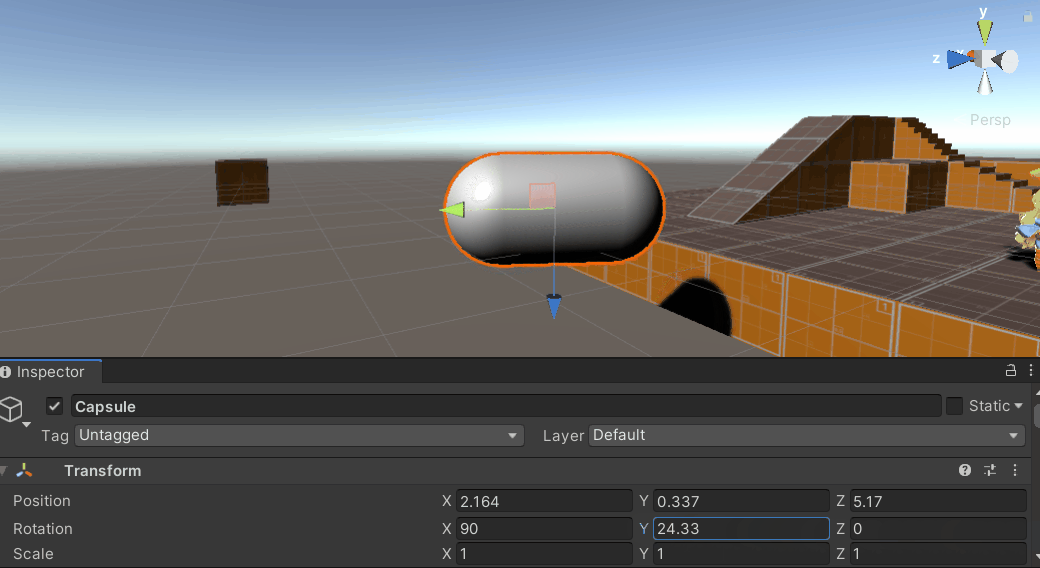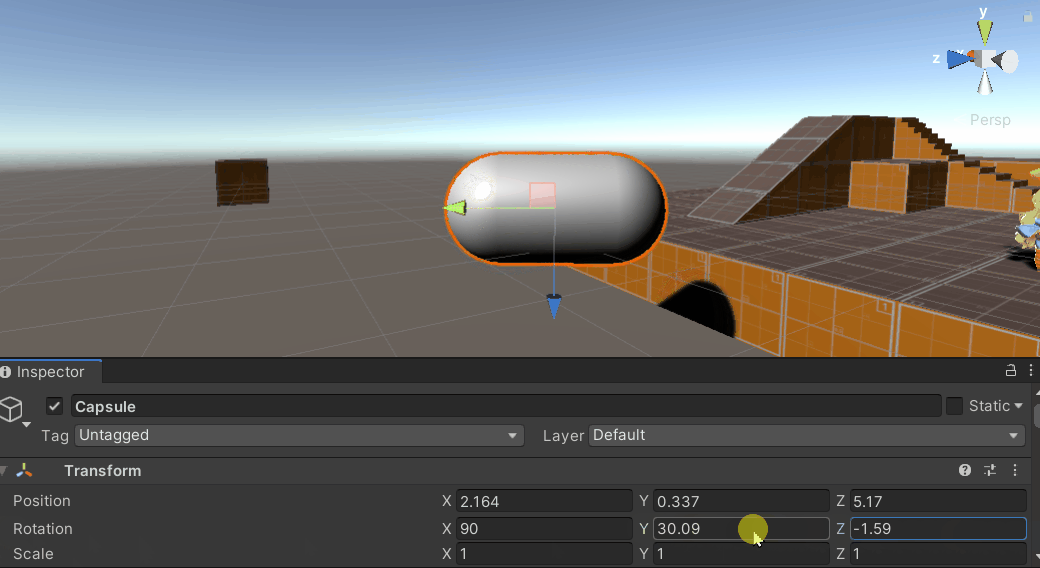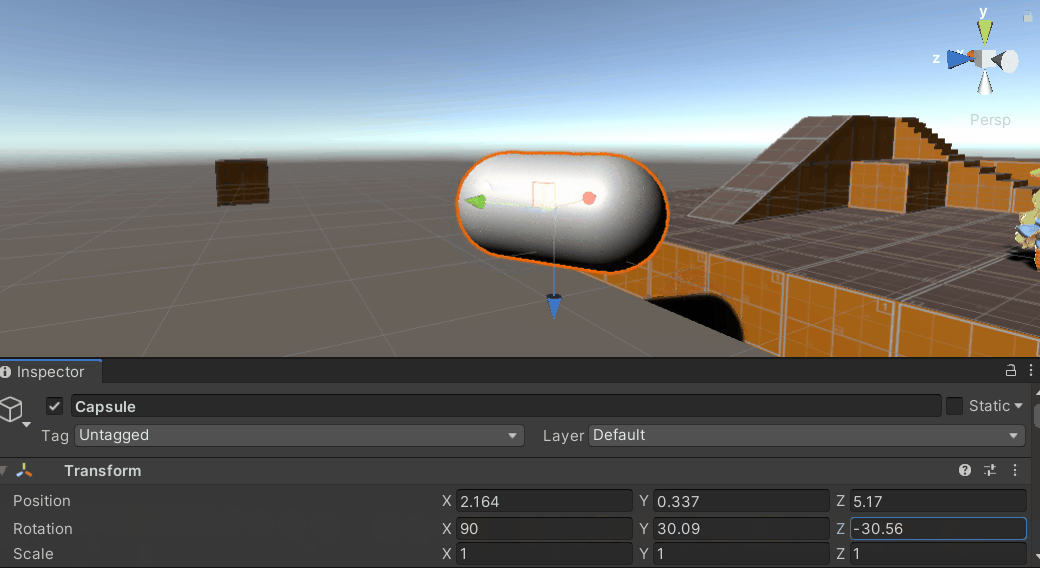
在不同的三维软件/游戏引擎中，由于各个软件底层规定的旋转顺序不同，万向锁的产生条件有些许不同，如UE4中使用左手系Z-up坐标系，按Z->Y->X的旋转顺序，固定Z轴旋转为绕惯性坐标系旋转，因此在物体绕中间轴Y轴到达90°或-90°附近时会发生万向锁问题。

总而言之，Unity中的万向锁问题的产生实质上是Y-up坐标系的设计原因与固定的旋转顺序导致的，这与3D数学上的万向锁问题有些不同，但旋转后的Z坐标轴和原来的Y坐标轴重合，使得旋转后的Z轴旋转可以由旋转前的Y轴旋转代替，这一点和3D数学上的万向锁问题是一致的。

3D数学上的万向锁问题

参考资料：Gimbal Lock

我们在表示欧拉角时将其写成矩阵乘法的形式，现在我们以X->Y->Z的固定旋转顺序，从数学角度上来看产生万向锁的过程：

\[E(yaw,pitch,roll)=R_z(yaw)R_y(roll)R_x(pitch) \]

以下表示坐标系均为右手坐标系，首先沿x轴旋转任意度数：

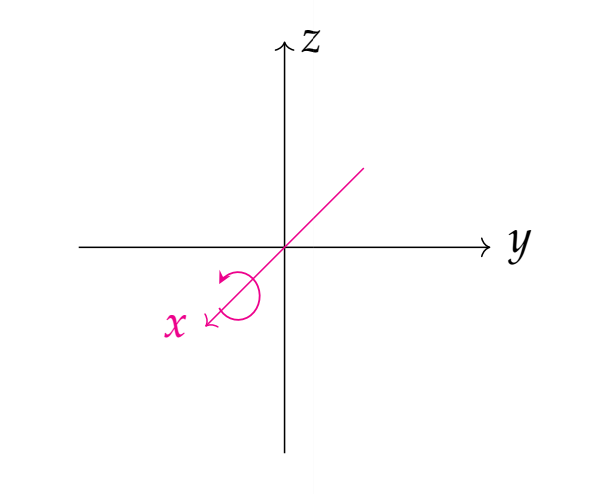
接下来，沿y轴旋转\(\pi/2\)弧度：

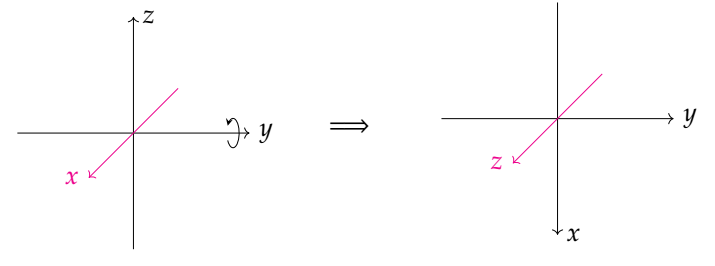
注意到，经过这一次的变换后，我们将z轴变换到原来x轴方向，而x轴变换到原来-z轴方向。

这个变换执行完成后，我们仅剩最后z轴上的旋转矩阵。然而，当前的z轴与原来的x轴重合，最后z轴的旋转与x轴的旋转可以等价，也就是说最后z轴的旋转可以由最开始x轴上的旋转所替代。从整个三维空间的世界坐标系来看，三次旋转变换仅覆盖了两个轴的旋转，丢失了一个轴上的自由度，这就是3D数学上的万向锁。

上面这个过程以矩阵乘法形式写出如下：

\[\begin{aligned} E(\alpha,\pi/2,\beta) &= R_z(\beta)R_y(\pi/2)R_x(\alpha) \\ &= \begin{bmatrix} cos\beta & -sin\beta & 0 \\ sin\beta & cos\beta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\-1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\alpha & -sin\alpha \\ 0 & sin\alpha & cos\alpha \end{bmatrix} \\ &= \begin{bmatrix} 0 & sin(\alpha-\beta) & cos(\alpha-\beta) \\ 0 & cos(\alpha-\beta) & -sin(\alpha-\beta) \\ -1& 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\-1 & 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(\alpha-\beta) & -sin(\alpha-\beta) \\ 0 & sin(\alpha-\beta) & cos(\alpha-\beta) \end{bmatrix} \\ &= R_y(\pi/2)R_x(\alpha-\beta) \end{aligned} \]

利用三角恒等变换，原本三个旋转矩阵所组成的变换化简成了两个变换矩阵。也就是说即使我们分别对x-y-z三轴进行了旋转，只要y轴上的变换角使得当前z轴与原来x轴对齐，我们就没有任何办法对最初的z轴进行旋转了。

万向锁问题在动态欧拉角旋转中都不可避免，故而使用四元数来规避万向锁问题是涉及三维旋转的很重要的一环。

为什么欧拉角会导致万向锁问题而四元数不会？严谨表述如下：

In formal language, gimbal lock occurs because the map from Euler angles to rotations (topologically, from the 3-torus T3 to the real projective space RP3 which is the same as the space of 3d rotations SO3) is not a local homeomorphism at every point, and thus at some points the rank (degrees of freedom) must drop below 3, at which point gimbal lock occurs. Euler angles provide a means for giving a numerical description of any rotation in three-dimensional space using three numbers, but not only is this description not unique, but there are some points where not every change in the target space (rotations) can be realized by a change in the source space (Euler angles). This is a topological constraint – there is no covering map from the 3-torus to the 3-dimensional real projective space; the only (non-trivial) covering map is from the 3-sphere, as in the use of quaternions.

https://en.wikipedia.org/wiki/Gimbal_lock

万向锁所导致的问题

欧拉角与万向锁 这篇文章中有大量动图，展示了在发生了万向锁的情况下仍使用动态欧拉角旋转到想要的位置，必须同时旋转三个轴向所导致的卷绕现象。

四元数

参考资料：

• 四元数与三维旋转
• 四元数
• 四元数的可视化

复数

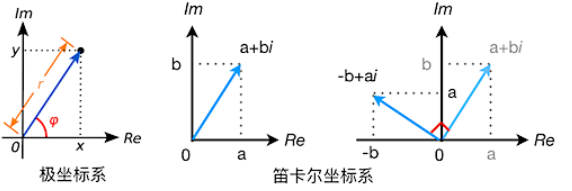
复数是一种复合的数字，\(C_{复数} = a + b \cdot i\) ，其中 a、b 为实数，\(i\) 为虚数，\(i^2 = -1\)

• 复数通过 实部 a 和 虚部 b 构成的二维虚平面，将一维的数扩展到二维平面

• \(i\) 只是区分 实部 a 和 虚部 b 的标记，这样可以把复数用二维的向量表示

  加法：\((a + bi) + (c + di) = (a + c) + (b+d)i\)

  乘法：\((a + bi) *(c + di) = (ac - bd) + (bc+ad)i\)

• 复数实际上就是对于\(\{1,i\}\)这个基（Basis）的线性组合（Linear Combination），通俗点来说就是对将1和i这两个基乘上标量后再相加的形式

• 复数乘以 \(i\) 的几何意义，在二维平面上逆时针旋转 90 度 \((a + b \cdot i) * i = a*i + b*i^2 = -b + a \cdot i\)

三维空间中的旋转——罗德里格旋转公式

上面已经探讨过使用欧拉角表示三维空间的旋转虽然直观却会导致万向锁问题，因而四元数在表示三维空间旋转的方式时采用轴角式（Axis-angle）的旋转。

v绕u旋转θ得到v'，轴角式旋转示意图如下：

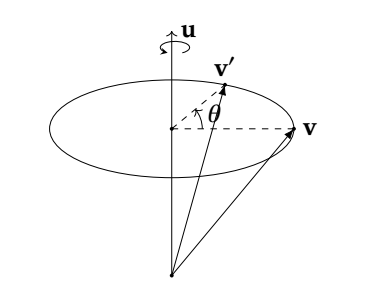
在轴角的定义中，\(\vec{u}\)为过原点的旋转轴，在实现中由于并不需要其模长而只需要其方向，一般将其约束为一个单位向量\(\vec{u}=(x,y,z),|\vec{u}|=1\)，\(\theta\)为旋转角度。

有了轴和角的定义，我们就可以看如何表示旋转：

1. 将v分解为平行于旋转轴u以及正交于u的两个分量

   \[\begin{aligned} v &= v_{||} + v_{\bot}\\ v_{||} &= proj_u(v) = {u \cdot v \over ||u||} \cdot {u \over ||u||} = {(u \cdot v)u \over ||u||^2} = (u \cdot v)u\\ v_{\bot} &= v - v_{||} = v - (u \cdot v)u \end{aligned} \]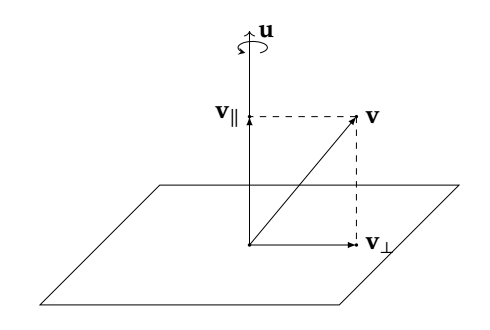
   

2. 将旋转后的v'也分解为平行与正交两个向量。构造一个同时正交于u和\(v_{\bot}\)的向量w，用于表示v'的垂直向量

   \[\begin{aligned} w &= u \times v_{\bot}\\ ||w|| &= ||u \times v_{\bot}|| \\ &= ||u|| \cdot ||v_{\bot}|| \cdot sin{\pi \over 2}\\ &= ||v_{\bot}|| \\\\ v_{\bot}' &= v_v' + v_w'\\ &= v_{\bot} \cdot cos\theta + w \cdot sin\theta \\ &= v_{\bot} \cdot cos\theta + (u \times v_{\bot})\cdot sin\theta \\ v_{||}' &= v_{||}= (u \cdot v)u \end{aligned} \]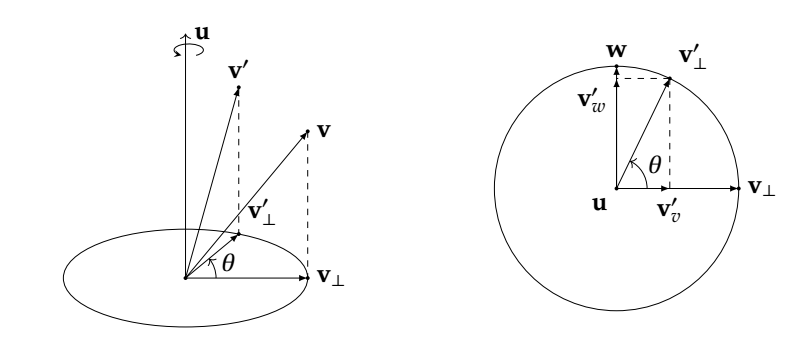
   

3. 结合1，2可得向量型的3D旋转公式：

   \[\begin{aligned} v'&=v_{||}' + v_\bot' \\ &=(u \cdot v)u + v_\bot \cdot cos\theta + (u \times v_\bot)sin\theta \\ &=v \cdot cos\theta + (u\cdot v)u(1 - cos\theta)+(u \times v)sin\theta \end{aligned} \]

   也叫做罗德里格旋转公式（Rodrigues' rotation Formula）。

四元数

四元数本质上就是一个三维复数，用于解决三维空间的旋转变化问题，带有三个虚部和一个实部，形式如下：

\[q=a+bi+cj+dk\quad(a,b,c,d∈\mathbb{R}) \]

其中，

\[i^2=j^2=k^2=ijk=-1 \]

并以此推出其循环对称性的其它性质，如下图（顺序：行*列）：

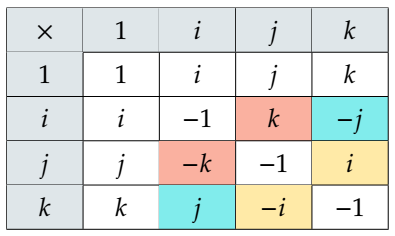
与复数类似，四元数其实就是对于基\(\{1,i,j,k\}\)的线性组合，也可以表示成四维向量\(q=\pmatrix{a\\b\\c\\d}\)，我们通常也将其实部和虚部拆开，写为标量和向量的有序对形式：

\[q=[s,\vec{v}].\quad(\vec{v}=\begin{bmatrix} x\\y\\z \end{bmatrix},s,x,y,z∈\mathbb{R}) \]

四元数矩阵乘法表示

设\(q_1={\pmatrix{a\\b\\c\\d},q_2=\pmatrix{e\\f\\g\\h}}\)，四元数相乘根据多项式乘法可以写作矩阵形式：

\[q_1q_2=\begin{bmatrix} a & -b & -c & -d \\ b & a & -d & c \\ c & d & a & -b \\ d & -c & b & a \end{bmatrix} \begin{bmatrix} e \\ f \\ g \\ h \end{bmatrix} \]

该变换等价于左乘\(q_1\)，由于四元数相乘不满足交换律，所以右乘\(q_1\)的变换是一个不同的矩阵：

\[q_2q_1=\begin{bmatrix} a & -b & -c & -d \\ b & a & d & -c \\ c & -d & a & b \\ d & c & -b & a \end{bmatrix} \begin{bmatrix} e \\ f \\ g \\ h \end{bmatrix} \]

形式类似，可以看作右下角3x3矩阵作了转置。

四元数乘法

由乘积结果：

\[q_1q_2=(ae-(bf+cg+dh))+(be+af+ch-dg)i\\+(ce+ag+df-bh)j+(de+ah+bg-cf)k \]

若令\(\vec{v}=\begin{bmatrix} b\\c\\d\end{bmatrix}\)，\(\vec{u}=\begin{bmatrix} f\\g\\h\end{bmatrix}\)，那么：

\[\begin{aligned} \vec{v} \cdot \vec{u} &= bf+cg+dh \\ \vec{v} \times \vec{u} &= \left| \begin{matrix} i & j & k \\ b & c & d \\ f & g & h \end{matrix} \right| \\ &=(ch-dg)i-(bh-df)j+(bg-cf)k \end{aligned} \]

对乘积结果由以上两式进行替换，可得以下定理：

\[对于任意四元数q_1=[s,\vec{v}],q_2=[t,\vec{u}],q_1q_2的结果是 \\ q_1q_2=[st-\vec{v} \cdot \vec{u}, s\vec{u}+t\vec{v}+\vec{v}\times\vec{u}] \]

该结果也叫格拉斯曼积（Grassmann Product），该结果实际上即为多项式相乘结果写为标量向量有序对形式即可。

纯四元数

仅有虚部，或者说实部为0的四元数。

\[v=[0,\vec{v}],u=[0,\vec{u}] \\ vu=[0-\vec{v} \cdot \vec{u},0+\vec{v} \times \vec{u}]=[-\vec{v} \cdot \vec{u}, \vec{v} \times \vec{u}] \]

逆和共轭

类似于复数的共轭，一个四元数\(q=a+bi+cj+dk\)的共轭为\(q^*=a-bi-cj-dk\)

四元数的逆，我们的目标就是找到\(q^{-1}\)使得\(qq^{-1}=1\)，利用共轭性质\(q^*q=||q||^2\)易推

\[qq^{-1}=1 \\ q^*qq^{-1}=q^* \\ ||q||^2q^{-1}=q^*\\ q^{-1}=\frac{q^*}{||q||^2} \]

如果\(||q||=1\)，即\(q\)是一个单位四元数，那么\(q^{-1}=q^*\)

四元数与3D旋转

回顾一下上面的轴角式旋转，现在开始将四元数与3D旋转关联起来。首先我们将一个向量v沿着一个用单位向量所定义的旋转轴u旋转θ度，我们将v拆分成正交与旋转轴的\(v_\bot\)以及平行于旋转轴的\(v_{||}\)。对着两个向量分别进行旋转，获得\(v_\bot'\)和\(v_{||}'\)，相加即得到旋转后结果\(v'\)。

我们将这些向量都定义为纯四元数：

\[\begin{aligned} v&=[0,\vec{v}] &v'=[0,\vec{v'}] \\ v_\bot&=[0,\vec{v_\bot}] & v_\bot'=[0,\vec{v_\bot'}] \\ v_{||}&=[0,\vec{v_{||}}] & v_{||}'=[0,v_{||}'] \\ u &= [0,\vec{u}] \end{aligned} \]

按之前推导的：

\[\vec{v_\bot'}=cos\theta \vec{v_\bot} + sin\theta(\vec{u} \times \vec{v_\bot})\\ \vec{v_{||}'}=\vec{v_{||}}\\ \vec{v'}=\vec{v_{||}'}+\vec{v_\bot'} \]

首先，需要将向量叉乘形式\(\vec{u} \times \vec{v_\bot}\)写成四元数乘法形式\(uv_\bot\) ，然后继续化简如下：

\[\begin{aligned} v_\bot' &= cos\theta v_\bot + sin\theta (uv_\bot) \\ &= (cos\theta+sin\theta u)v_\bot \quad(注意顺序，四元数乘法不遵守交换律)\\ \end{aligned} \]

此处，我们可以将\((cos\theta+usin\theta)\)写成四元数形式\(q=[cos\theta,sin\theta \vec{u}]\) ，即得到正交分量的四元数型3D旋转公式：

\[当\vec{v_{\bot}}正交于旋转轴\vec{u}时，旋转\theta角度之后的v_{\bot}'的四元数型表示：\\ 令v_{\bot}=[0,\vec{v_{\bot}}],q=[cos\theta,sin\theta \vec{u}],则v_{\bot}'=qv_{\bot} \]

而由\(\vec{v_{||}'}=\vec{v_{||}}\)可知平行分量的四元数型3D旋转公式：

\[v_{||}'=v_{||} \]

可得：

\[v'=v'_{||}+v'_{\bot}=v_{||}+qv{_\bot} \]

虽然可以像上面推向量型的3D旋转公式一样将\(v_{||},v_{\bot}\)利用几何关系用\(v\)和\(u\)表示出来，但这里用另外的办法来化简：

1. 引入一个新四元数\(p=[cos(\frac{1}{2}\theta),sin(\frac{1}{2}\theta)\vec{u}]\)，\(q=p^2=[cos\theta,sin\theta\vec{u}]\)（\(p^2\)为两个旋转的叠加，易证）

2. 由于\(p,q\)均为单位四元数，即\(p^{-1}=p^*\)，可得：

   \[\begin{aligned} v'&=v_{||}+qv_{\bot} \\ &= 1 \cdot v_{||}+qv_{\bot} \\ &= pp^{-1}v_{||}+p^2v_{\bot} \\ &=pp^*v_{||}+p^2v_{\bot} \end{aligned} \]

3. 接下来需证以下两个性质 ①\(qv_{||}=v_{||}q\) ②\(qv_{\bot}=v_{\bot}q^*\) ，由格拉斯曼积的公式可知影响四元数左乘右乘的关键因素在于向量部分的叉乘，由\(\vec{u} \times \vec{v_{||}} = \vec{v_{||}} \times \vec{u}= 0,\quad \vec{u} \times \vec{v_{\bot}} = \vec{v_{\bot}} \times (-\vec{u})\) 易证①②

   利用性质①②可作以下变形：

   \[\begin{equation} \nonumber \begin{aligned} v' &= pp^*v_{||}+ppv_{\bot} \\ &= pv_{||}p^*+pv_{\bot}p^* \\ &= p(v_{||}+v_{\bot})p^* \\ &= pvp^* \end{aligned} \end{equation} \]

四元数型3D旋转公式：

\[任意向量\vec{v}沿着以单位向量定义的旋转轴\vec{u}旋转\theta度之后的v'的四元数型表示：\\ 令v=[0,\vec{v}],q=[cos(\frac{1}{2}\theta),sin(\frac{1}{2}\theta)\vec{u}],则v'=qvq^*=qvq^{-1} \]

事实上，该等式也完全等价于之前所推的罗德里格旋转公式：

\[qvq^*=[0,cos\theta\vec{v}+(1-cos\theta)(\vec{u} \cdot \vec{v})\vec{u} + sin\theta(\vec{u} \times \vec{v})] \]

至此，我们得到用四元数表示一次三维空间旋转的基本公式。

四元数旋转的复合

假设\(q_1,q_2\)分别表示沿着不同轴，不同角度旋转的四元数。我们进行\(q_1\)的变换如下：

\[v'=q_1vq_1^* \]

接下来对\(v'\)作\(q_2\)变换：

\[\begin{equation} \nonumber \begin{aligned} v''&=q_2v'q_2^* \\ &=q_2q_1vq_1^*q_2^* \end{aligned} \end{equation} \]

由引理\(q_1^*q_2^*=(q_2q_1)^*\)（可自行证明）可得：

\[\begin{equation} \nonumber \begin{aligned} v''&=q_2q_1vq_1^*q_2^*\\ &=(q_2q_1)v(q_2q_1)^* \\ &=q_{net}vq_{net}^* \end{aligned} \end{equation} \]

可以得到一个复合旋转\(q_{net}\)，但对于该复合旋转的理解并不是按\(q_1,q_2\)进行变换的两次旋转，而是一个仅旋转结果相同的等价旋转。

双倍覆盖（Double Cover）

• 对任意单位四元数q，q与-q代表的是同一个旋转。若q表示的是沿着旋转轴\(\vec{u}\)旋转θ度，那么-q代表的是沿着相反的旋转轴\(-\vec{u}\)旋转\((2\pi-\theta)\)度。
• 对于这种性质，我们常称单位四元数双倍覆盖（Double Cover）了3D旋转，或者说单位四元数与3D旋转之间有2对1满射同态关系。所有的单位四元数都对应一个3D旋转。

其它

关于四元数插值、四元数,欧拉角,矩阵三种形式间的转换等等一部分其它内容，暂时先留个坑，随缘填。