算法题——冗余连接2

冗余连接2

题干

在本问题中，有根树指满足以下条件的 有向 图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi 的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]
示例 2：

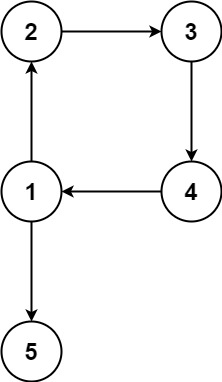
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

思路

需要考虑成环的边和造成冲突的边。

    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int len = edges.size();
        //papa表示题干中的边所给出的父节点和子节点的关系，expapa表示由有向边形成的并查集
        vector<int> papa(len+1);
        vector<int> expapa(len+1);
        for(int i=1; i<=len; ++i)
        {
            papa[i]=i;
            expapa[i]=i;
        }
        int conflict=-1;
        int cycle=-1;
        for(int i=0; i<len; ++i)
        {
            int v1=edges[i].front(), v2=edges[i].back();
            if(papa[v2]!=v2)
            {
                conflict=i;
            }
            else
            {
                papa[v2]=v1;
                if(find(expapa,v1)==find(expapa,v2))
                {
                    cycle=i;
                }
                else
                {
                    merge(expapa, v1, v2);
                }
            }
        }
        if(conflict==-1)
        {
            return {edges[cycle].front(), edges[cycle].back()};
        }
        else
        {
            if(cycle==-1)
            {
                return {edges[conflict].front(), edges[conflict].back()};
            }
            else
            {
                return {papa[edges[conflict].back()], edges[conflict].back()};
            }
        }
        return vector<int> {};
    }
    int find(vector<int> &f, int index)
    {
        if(f[index]!=index)
        {
            f[index]=find(f,f[index]);
        }
        return f[index];
    }
    void merge(vector<int> &f, int v1, int v2)
    {
        f[find(f,v1)]=find(f,v2);
    }