算法题——冗余连接

684.冗余连接

题干

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

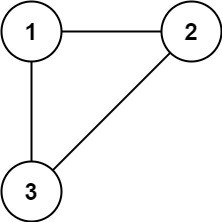
输入: edges = [ [1,2], [1,3], [2,3] ]
输出: [2,3]

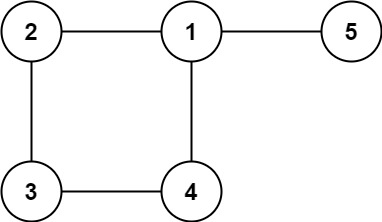
输入: edges = [ [1,2], [2,3], [3,4], [1,4], [1,5] ]
输出: [1,4]

思路

对于一个包含n个节点的图，至少需要n-1条边才能使图连接起来，本题中共有n条边，n个节点，那么出现的第一条使得图成环的边就是最后一条使得图成环的边，即该边就是答案。

在无环图中考虑连通性使用并查集，在有向图中考虑依赖性使用dfs、bfs或拓扑排序。

vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int len=edges.size();
        vector<int> p(len+1);
        for(int i=1; i<=len; ++i)
        {
            p[i]=i;
        }
        for(auto &edge : edges)
        {
            int v1=edge.front(), v2=edge.back();
            //查找两个节点v1和v2是否属于同一个集合
            if(Find(p,v1)!=Find(p,v2))
            {
                Union(p,v1,v2);
            }
            else
            {
                return edge;
            }
        }
        return vector<int>{};
    }
    int Find(vector<int>& p, int index)
    {
        //如果index的parent不是index，说明index已经归到某个集合中，继续查找index的parent
        //最顶层的index的parent是其本身
        if(p[index]!=index)
        {
            p[index]=Find(p,p[index]);
        }
        return p[index];
    }
    void Union(vector<int> &p, int v1, int v2)
    {
        //定义联合为将v1所在的集合的父节点设置为v2所在集合的父节点，这样两个集合就连接了
        p[Find(p,v1)]=Find(p,v2);
    }