图形 1.2.1 向量基础
图形 1.2.1 向量基础
向量定义
- 向量是有大小和方向的有向线段
- 向量没有位置,只有大小和方向
- 向量的箭头是向量的结束,尾部是向量的开始
- 向量描述的位移可以被认为是与轴平行的位移序列
- 向量表示:三维(ax, ay, az),二维(ax, ay)
尾部是向量的开始,比如向量AB,是从点A到点B,A是开始也是向量尾部,向量AB是点B坐标减去点A坐标。

向量与标量
向量有方向,标量没有。
向量与点
- 点:有位置但没有实际大小或方向。
- 向量:没有位置但是有实际大小或方向。
点可以看作从原点出发的向量。
零向量
- 唯一大小为零的向量
- 唯一没有方向的向量
- 零向量不是一个点,因为它没有确定的位置
- 零向量表示没有位移,类似零标量表示没有数量
标量与向量的计算
不能加减,只能乘除。乘除时标量与向量的每个分量计算即可。
向量的模长
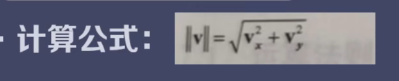
n维向量以此类推。二维向量模长计算实际上类似勾股定理,构成三角形进行计算。
标准化向量
标准化向量就是大小为1的向量,也叫单位向量,适用于只关心其方向但不关系大小的情况,例如法线。
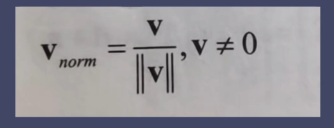
向量与向量加减法
同样维度的向量才能计算,对应分量相加减。
计算两点间距离:距离公式

可以看作计算两个向量相减得到的新向量的模长。
向量的点积
又称为点乘、内积,就是分量对应相乘。
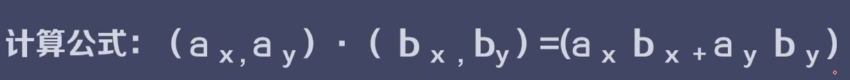
点乘结果是一个标量,并且满足交换律。
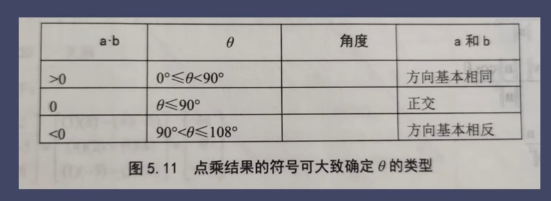
点积的几何意义和向量投影
点乘结果越大,说明两个向量夹角越小。

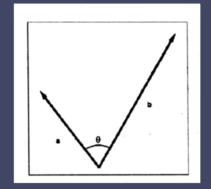
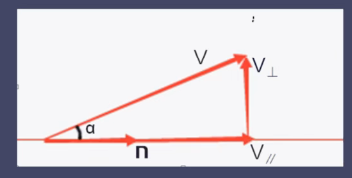
向量投影就是一个向量在另一个向量上的投影长度。
这个夹角是两个向量头部相接的夹角。
兰伯特光照模型
Lambert光照模型是目前最简单通用的模拟漫反射的光照模型。

这里光照反方向L向量与法线N向量都是单位向量(法线是垂直于物体表面的),cos函数从0°到180°变化是1到-1,L向量和N向量点积结果就是1到-1,根据L与N之间的夹角变化。
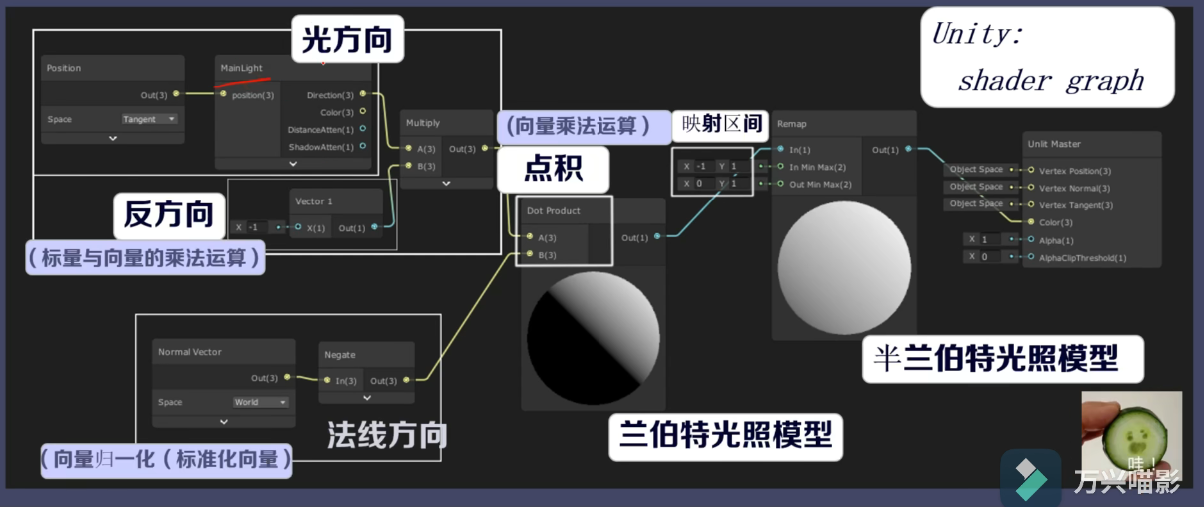
先获取光照方向,与标量相乘取反反向,然后与归一化的法线向量点积,右边是调整。
向量的叉积运算
仅用于3D向量。

分量交叉相乘最后相减,结果是向量,叉乘的结果垂直于原来两个向量确定的平面。
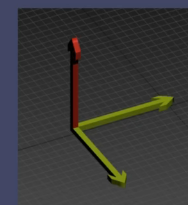
向量叉积大小于方向的判断
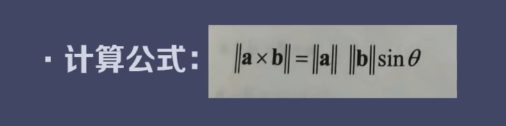
sin的角度是从a向量到b向量顺时针旋转的角度


 浙公网安备 33010602011771号
浙公网安备 33010602011771号