只使用7次比较，完成5个元素的排序

背景

考虑快速排序为什么最坏情况下时间复杂度为O(n²)？这是因为每次进行划分的时候，都有一个部分大小为0（或者说为一个常数）。如果我们能够找到一种时间复杂度为O(n)的划分方法，使得划分后的两部分大小均为Θ(n)，则快速排序的时间复杂度总能为Θ(nlogn)。

假设我们能够用非常小的代价寻找5个元素中的中位数，则我们可以递归的将原数组划分为大小为5的子数组，寻找每个子数组的中位数。容易证明，通过这种方式最终找到的中位数，至少存在Θ(n)的元素比它小（大）。

插入排序的一种简单改进

首先介绍插入排序的一种简单的改进，这一方法将在稍后用到。插入排序将数组划分为两部分：已序部分和待排序部分。每次从待排序部分中取出一个数，插入到已序部分中并保持其有序性。可以想到，在已序部分中使用二分查找，则可以在O(logn)的时间内，找到待插入元素的位置。

突破点

这里有一个小技巧，是仅使用7次比较，完成5个元素的排序的基础。

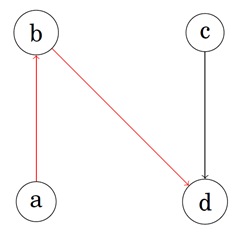
考虑对3个元素排序，至少需要几次比较？答案是3次。但是如果有4个元素，要求对其中的3个元素建立全序关系，至少需要几次比较呢？答案仍然是3次。方法如下。假设有四个元素a、b、c、d。如下图所示，在a和b之间进行一次比较，在c和d之间进行一次比较，将这两次比较中较大的元素再进行一次比较，则至少有3个元素能够确定全序关系。

现在，我们仅通过3次比较，不仅得出了3个元素的全序关系，还知道另外一个元素与这3个元素中的一个元素的序关系。

完整算法

假设有5个元素：a、b、c、d、e。

首先，我们使用3次比较，确定3个元素的全序关系，并且还额外的知道了另外一个元素与这3个元素中的一个元素的序关系。例如：a < b < c且a < d。

接着，我们使用折半查找将e插入到已序序列a、b、c中，至多需要2次比较。然后得到已序序列a、b、c、e。

由于最开始我们已经知道了剩下的未排序元素与已序序列中一个元素的序关系，因此至少可以排除掉一个元素。相当于将剩下的未排序元素插入到一个长度为3的已序序列，至多需要2次比较。例如将d插入到已序序列a、b、c、e中，已知a < d，则只需考虑将d插入到已序序列b、c、e中。

综上所述，至多需要7次比较，即可完成5个元素的排序。

总结

有的时候，有些问题看似是在不可能中寻找可能，实际上却是需要我们换一种角度来看待问题。正所谓山穷水复疑无路，柳暗花明又一村。只要我们不放弃，从多种角度思考问题，总会有解决的方法的。