应用密码学复习笔记

前言

大部分是个人理解，如有错误，欢迎指出，欢迎讨论交流。

1.一些名词翻译

保密性confidentiality

保密性（Confidentiality）：这个术语包含了两个相关的概念：
数据保密性：确保隐私或者秘密信息不向非授权者泄露，也不被非授权者所使用。
隐私性：确保个人能够控制或确定与其自身相关的哪些信息是可以被收集、被保存的，这些信息可以由谁来公开以及向谁公开.

完整性integrity

完整性（Integrity）：这个术语包含两个相关的概念：
数据完整性：确保信息和程序只能以特定和授权的方式进行改变。
系统完整性：确保系统以一种正常的方式来执行预定的功能，免于有意或者无意的非授权操纵。

可用性availability

可用性（Availability）：确保系统能工作迅速，对授权用户不能拒绝服务

真实性authenticity

真实性（Authenticity）：一个实体是真实性的、是可被验证的和可被信任的特性；对传输信息来说，信息和信息的来源是正确的。也就是说，能够验证那个用户是否是他声称的那个人，以及系统的每个输人是否均来自可信任的信源。

可追溯性accountability

可追溯性（Accountability）：这一安全目标要求实体的行为可以唯一追溯到该实体。这一属性支持不可否认性、阻止、故障隔离、人侵检测和预防、事后恢复，以及法律诉讼。因为无法得到真正安全的系统，我们必须能够把安全泄露追查到负有责任的一方。系统必须保留他们活动的记录，以允许事后的审计分析来跟踪安全事件或者解决争执。

被动攻击passive attacks

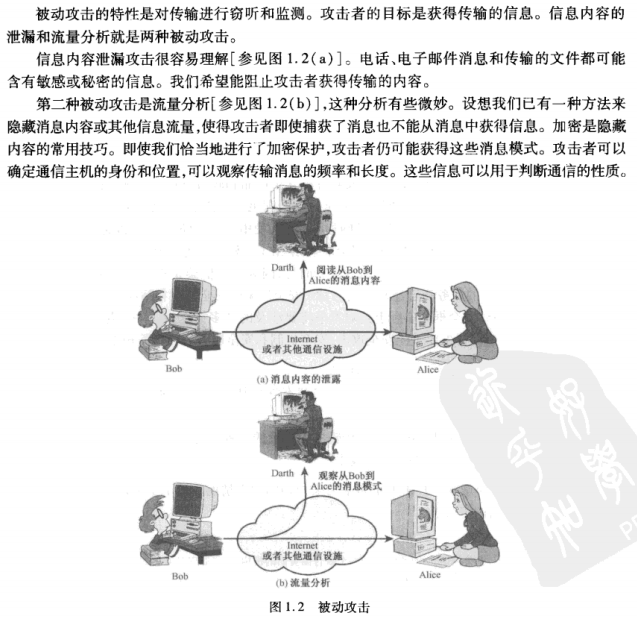
应用密码学

主动攻击active attacks（伪装masquerade，重放/重播replay，消息篡改/消息修改data modification）

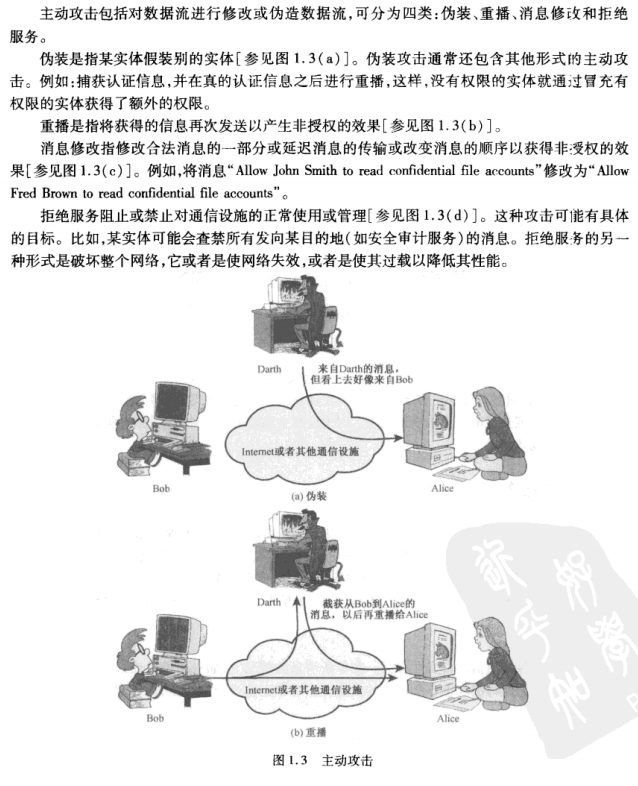
应用密码学

2.计算题（代替技术，置换技术）

应用密码学

2.1代替技术Substitution Technique

2.1.1简单的位移密码caesar cipher

对明文p,有加密过程\(c=E(k,p)=(p+k)mod26\)，其中k为位移量，即密钥。
对密文c，有解密过程为\(c=D(k,c)=(c-k)mod26\)，其中k为位移量，即密钥。
对于26个英文字母，k的范围是0~26，较为不安全。

应用密码学

2.1.2单表密码Monoalphabetic Cipher

使用字母表完成明文到密文的映射，缺点是会保留明文例如字母频率的特征。
应用密码学

2.1.3单表密码改进Playfair Cipher （普莱费尔密码）

这个密码的生成分三步：

确定密钥，生成字母表。
假设密钥是a lucky day，字母表规则为先按行(按列也许，这里按课本上来)填入密钥字母，若有重复则去重，然后按顺序填满5x5的字母表，其中i/j（这个也有不同的写法，这里也按课本上来）放在同一格，所以可生成字母表如下:

a l u c k

y d b e f

g h i/j m n

o p q r s

t v w x z
拆分明文。
如有明文see you tomorrow，拆分成se ey ou to mo rx ro wx
查表加密。
如对述明文，按以下规则查表替换。
- 若两个字母在同一行，则分别用右边的字母替代。
- 若在同一列，用其下面的字母代替。
- 若非以上两种情况，用当前字母的所在行，另一字母的所在列替换。
如se替换成rf，ey替换成fd,to替换成at。
上述明文可替换成rf fd qa at rg xc sp xz。
若遇到替换后为i/j格，可任意选用i或者j来替换。

a	l	u	c	k
y	d	b	e	f
g	h	i/j	m	n
o	p	q	r	s
t	v	w	x	z

应用密码学

2.1.4希尔密码hill cipher

暂时没看，mark here

2.1.5维吉尼亚密码vigenere cipher 多表代替加密

简单来说，假设明文p长度为n，准备一个密钥k长度也为n，有：
\(C = C_0，C_1，...，C_(n-1) = E(K,P) = E[(K_0,K_1,...,K(n-1)),(P_0,P_1,...,P(n-1))]\)
\(其中C_0=（P_0+K_0）mod 26\)
这样就能获得\(C =(C_0,C_1,...,C_(n-1))\)
解密过程:
\(P=D(C,K) =(C-K) mod26\),
例：
\(P=A,K=C,加密C=E(P,K)=(0+2)mod26=2=C,解密C=D(C,K)=(2-2)mod26=0=A\)

2.2置换技术Transposition Technique

2.2.1栅栏密码 rail fence cipher

例如有明文p=hello world
交错写成：
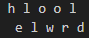
应用密码学
读出密文k=hloolelwrd

2.2.2行置换密码row transposition cipher

课本上只说了加密，那就只看加密了。
例如有明文attackatnoon,密钥k为645123,则有:

6	4	5	1	2	3
a	t	t	a	c	k
a	t	n	o	o	n

置换后：

6	4	5	1	2	3
a	c	k	t	t	a
o	o	n	t	n	a

读出密文为:ackttaoontna

3.给定HMAC的示意图，解释关键参数的获得方法

3.1消息认证码(Message Authentication Code,MAC),是什么

这部分内容和数字签名有点像，懒得划页面，留个跳转锚回去

MAC（Message Authentication Code）是一种用于对消息进行身份认证的技术。MAC是一种加密哈希函数，它使用一个密钥和消息作为输入，生成一个固定长度的字符串作为输出。这个输出称为MAC值，用于验证消息的完整性和真实性。

MAC的基本原理是，发送方使用密钥对消息进行哈希运算，生成MAC值，并将该值与消息一起发送给接收方。接收方使用相同的密钥和接收到的消息来计算MAC值，然后将计算得到的MAC值与接收到的MAC值进行比较。如果两者匹配，就表明消息没有被篡改，并且发送方是合法的。

MAC通常用于保护通信中的消息免受篡改的风险。它在安全协议和通信协议中被广泛使用，例如在TLS/SSL中用于保护网络通信，或在数字签名中用于验证文档的真实性。MAC的安全性依赖于使用的哈希函数和密钥的安全性。

该技术假设两个通信方，比如 A 和 B，共享一个称为 K 的共同秘密密钥。当 A 需要向 B 发送消息时，它根据消息和密钥计算 MAC 值，如下所示：

\(MAC=C(K,M)\)
其中：
M是输入消息,C是 MAC 函数,K是共享的秘密密钥,MAC是消息认证码
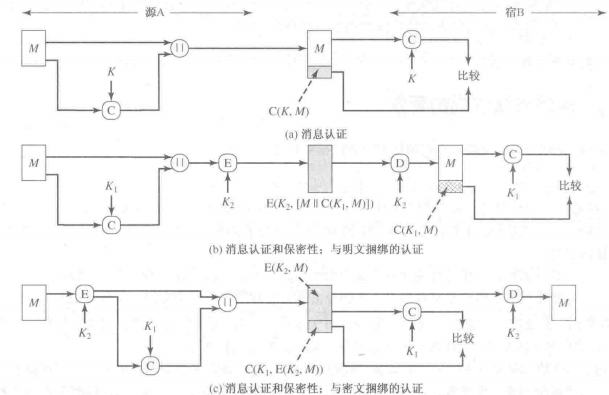
应用密码学

对于a，分析过程如下：
在计算\(C(M,K)\)后，将MAC附加在M后直接发送，接收方收到M+MAC后，对收到的M再次计算MAC`，然后对MAC`和MAC做对比，若相同，可认为消息未被篡改，该消息确实由正确的发送方发出，因为密钥只有双方知道，其他人不能计算MAC值。
a只适用于对消息做认证，不能提供保密性，因为整个过程中消息以明文形式传输。
对于b，分析如下：
先计算MAC，然后附加在M上，再使用E一起加密，就受访收到密文后，使用D解密，对获得的M再次计算MAC`,对MAC和MAC`，进行比较，若相等，可认为消息来源可信且消息未被篡改。
b克服了a的部分缺陷，对消息进行了加密，这种情况需要两个密钥，且收发双方共享。
对于c，分析如下：
先对明文M进行加密，然后计算MAC，附加在密文后发送，收方接收到消息后，对收到的密文计算MAC`,若MAC=MAC`,可认为消息未被篡改，接着就是收方对密文进行解密。
一般认为b方案会比c更好，一是b方案较之c方更能阻挡一些已知明文攻击或者选择明文攻击，二是c方案可能会泄露明文内容的信息，因为攻击者可以直接观察到密文和MAC。

3.2基于Hash函数的MAC:HMAC（MACs Based on Hash Functions: HMAC）

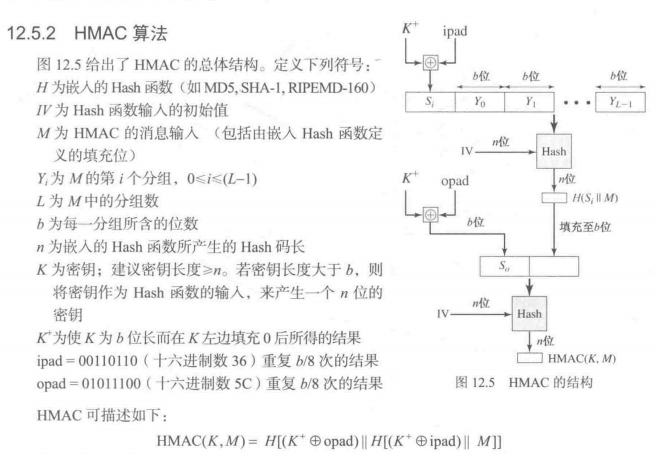
应用密码学

其工作流程大致如下：

当K的长度短于b时，往K的右边填充0，得到b位的K+，当K的长度大于b时，先对K进行散列，再进行填充。

例如有K160位，b=512，填充0共44个字节到左边（44=（512-160）/8，1字节8位）
K+与ipad进行异或

ipad=(0x36||0x36||...||0x36)，这一步获得分组S_i_，可称呼为内部哈希
ipad为8位。
将M附在S_i_后
将H作用在上一步获得的结果
将K+与opad进行异或

opad = （0x5c||0x5c||...||0x5c），这一步获得分组S_0_，可称呼为外部哈希
opad为8位。
将步骤4获得的Hash码附着在S_0_后。
将H作用在上一步获得的结果，并且输出该值为HMAC

4.Hash函数的基本性质，SHA-512执行过程关键步骤或运算

4.1Hash函数的基本性质

单向性

对预先指定的Hash值找不到对应的数据块。（难以通过已知hash值推出原值）
抗碰撞性

找不到两个不同的数据块对应相同的Hash值。（难以找到不同值对应相同hash值）

4.2 SHA512的计算

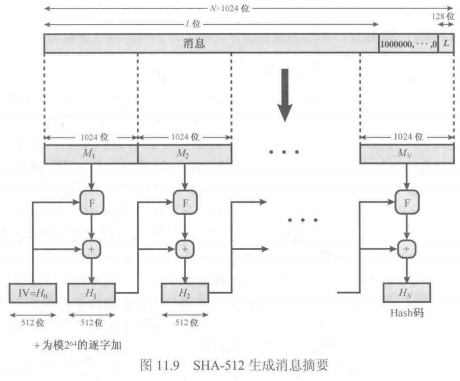
应用密码学

附加填充位
填充消息长度模1024和896同余，即假设消息长度为L位，有需要填充x位使得 L + x \(\equiv\) 896 mod 1024.
此时若有x=0时，L和896正好模1024同余，仍然要继续填充，填充的x位数在1~1024之间，填充时由一个1和后续的0组成。
附加长度
在第一步获得的消息后再附加一个128位的无符号数，其记录了原消息L的长度。
这两步生成了一个长度为 N x 1024 的消息，所以拓展消息的长度为 N x 1024 .
初始化Hash缓冲区
使用8个64位的寄存器保存Hsh函数的中间结果和最终结果，其中存有初始值如下。
以1024位的分组为单位处理消息

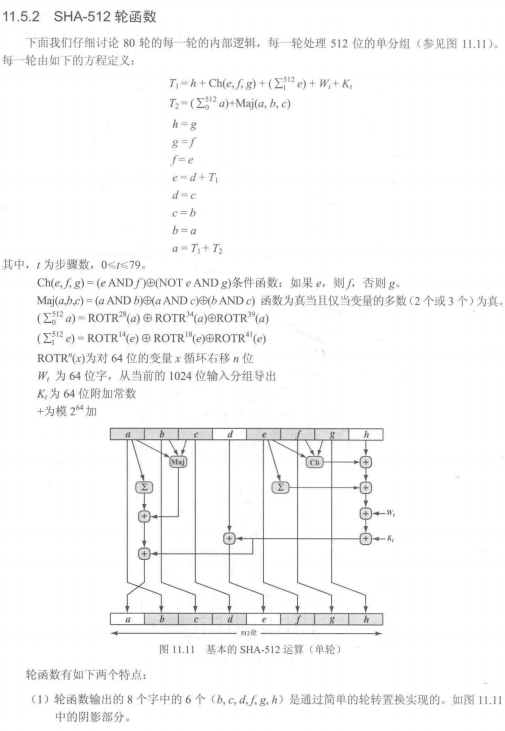
有空再看，mark here！！！！！！！！！！！！
输出

4.3 SHA512的一个例子

该例来自课本。
应用密码学

5. AES步骤相关

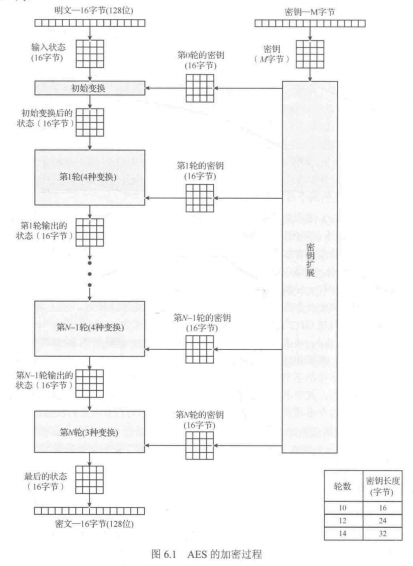
应用密码学

5.1 流程简述

仅为个人理解，若有错误请指出。

先将密钥和明文写成矩阵形式，按列填入。
密钥作密钥拓展，此时明文矩阵和第0轮密钥矩阵做异或，,即做第0轮轮密钥加获得状态0。
状态0做字节替换，行移位和列混淆，最后和第1轮拓展密钥做异或,即做第1轮轮密钥加获得状态1。
如此重复，获得状态n，即为密文。

5.2 各项实现

5.2.1 密钥拓展

例：

假设密钥为：2b7e151628aed2a6abf7158809cf4f3c

写成矩阵为：

2b	28	ab	09
7e	ae	f7	cf
15	d2	15	4f
16	a6	88	3c

有W0=2b731616,W1=28aed2a6,W2=abf71588,W3=09cf4f3c.
可以发现这是按列获取了密钥矩阵的数值，接下来的操作就是按列生成接下来的W4,W5,...Wn.
生成规则如下：

对第n列，0 \(\equiv\) n mod4,有：
Wn = Wn-4 \(\bigoplus\) g(Wn-1)
其中，g函数的作用是将其中内容左移一个字节，接着与S盒做字节替换，然后和Rcon向量异或。过程如下：
W3` =cf4f3c09，W3`` = 8a84eb01,W3`` \(\bigoplus\) Rcon[0] = 8b84eb01.
W4 = W3``` \(\bigoplus\) W0 = a0fafe17.
其中Rcon = [01,02,04,08,10,20,40,80,1b,36],进行异或操作的时候往右边填充0补齐。
如Rcon[0] = 0000 0001 0000 0000
对其他列，有：
Wn = Wn-4 \(\bigoplus\) Wn-1

5.2.2 轮密钥加

这个的规则较为简单，就是待加密信息和密钥矩阵异或。

5.2.3 字节替换

字节替换需要获取S盒，这里就不描述S盒的生成了，S盒是一个固定的矩阵。

例如对6a做字节替换，找到S盒中[6,a]项做替换即可。

5.2.4 行移位

这个实现也挺简单的，待加密信息的第一行不位移，第二行左移一位，第三行左移两位，第三行左移三位。

5.2.5 列混淆

最麻烦的部分，简单来说是让待加密信息左乘一个固定的矩阵如下：

02	03	01	01
01	02	03	01
01	01	02	03
03	01	01	02

但是注意，进行乘算时，乘法和加法都是定义在Gf(2^8)的乘法，加法即为异或，乘法有特殊的运算规则。

例如02 * 87，可以看成左移一位，低位补0；同时，若87的最高位为1，最后的结果还要异或1b(00011011)。

03 * 6e 可以看成 (02 * 68) \(\bigoplus\) 68，左移时注意原始最高位是否为1，是的话和0x1b异或以后再和自身异或.

5.3 解密相关

AES的解密步骤和加密同，这是因为对同一个数异或两次，还等于它本身。
需要注意的是，在进行字节替换的时候涉及到的是逆S盒，行移位的方向也变了，对于列混淆也是做成另一个矩阵，但是由于应该不考，懒得看了，知道有就行。

6. RSA 算法和 Diffie-Hellman 密钥交换相关

6.1 RSA算法相关

RSA算法的过程可以用以下式子表示：

\(加密：C = M^e\ mod\ N\qquad 解密：M=C^d \ modN=(M^e)^d\ mod\ N\)

其中，C为密文，M为明文，e、n和d分别为密钥对内的参数，关系为\(ed \equiv 1mod\ \phi(N)\)

对于N，有N的生成如下：

选定素数p，q（一般是选定大素数），使 \(p * q = N\ ,\ \phi(N)=(p-1)(q-1)\)。

对于e，d，其中e是选定的，d由计算得出，有 \(d = e^{-1} \equiv \phi(N)\)，即ed模N互逆。

在RSA中，密钥对分别为PU={e,N},PR={d,N},其中e，N公开，用于加密；d不公开，只有接收方持有，用于解密。

6.2 Diffie-Hellman 密钥交换相关

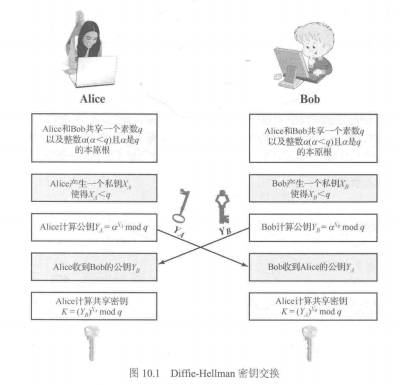
应用密码学

对一素数p和其本原根a，有密钥交换算法如下：

p和a为公开元素。
A和B都生成自己的私钥分别为\(X_A\)\(X_B\),要求\(X_A\)\(X_B\)都小于q。
A和B都计算自己的公钥\(Y_A\)\(Y_B\)并且发送给对方，计算方式如下：
\(Y_A = a^{X_a}\ mod\ q\)
双方接收到对方发送过来的公钥后，即可计算共享密钥K如下：
\(K = (Y_B)^{X_A}\ mod\ q\)

使用这种方式，AB双方计算出来的K是相等的，对于K，有如下计算结果都能获得K：
应用密码学

7. 验证签名算法的有效性

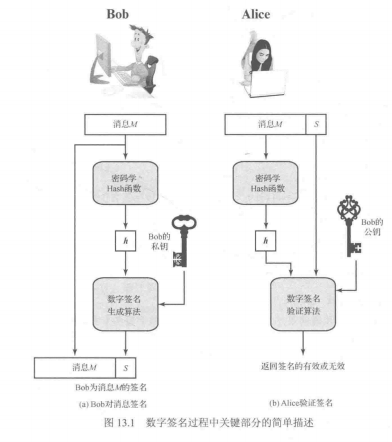
应用密码学

这是数字签名算法的大概流程，看起来和MAC的过程类似，但不同的是MAC的生成和验证使用的是发送和接收双方共有的元素K，而数字签名中，数字签名由发送方的私钥生成，接收方使用发送方的公钥验证签名是否有效。

这里链接到上文提及MAC的地方，验证思路是类似的。

8. 线性反馈移位寄存器(LFSR)生成随机序列

在摘录图片时，大多图片的来源是《密码编码学与网络安全——原理与实践(第七版)》，但本书并没有关于此内容的描述，相关内容在第八版才被加入。

对n位LFSR，有最大周期\(N = 2^n -1\).

例：

假设有四位寄存器\(B_0,B_1,B_2,B_3,有f(B_0,B_1,B_2,B_3)=B_0\bigoplus B_1,即P(X)=1+X+X^4,假设初始态为\{1000\}\)。

有输出序列情况如下：

N	\(B_3\)	\(B_2\)	\(B_1\)	\(B_0\)	\(B_0\bigoplus B_1\)	OUTPUT
0	1	0	0	0	0	0
1	0	1	0	0	0	0
2	0	0	1	0	1	0
3	1	0	0	1	1	1
4	1	1	0	0	0	0
5	0	1	1	0	1	0
6	1	0	1	1	0	1
7	0	1	0	1	1	1
8	1	0	1	0	1	0
9	1	1	0	1	1	1
10	1	1	1	0	1	0
11	1	1	1	1	0	1
12	0	1	1	1	0	1
13	0	0	1	1	0	1
14	0	0	0	1	1	1
15	1	0	0	0	0	0

得到的M序列为:0001001101011110

其中，每一步的寄存器的结果都往右移一位，首位寄存器的结果为上一轮\(f(B_0,B_1,B_2,B_3)=B_0\bigoplus B_3\)的输出；OUTPUT位与末位\(B_0\)相同。

m序列即为完整执行\(N = 2^n -1\)后的结果。

写段伪代码来辅助理解。

#做辅助理解用
m = []
b[3]=[1,0,0,0]  #len(b)-1 = 15

for i in range(0,)pow(2,len(b)-1):
  m.append(b[3])
  temp = b[2]^b[3]
  b[0],b[1],b[2],b[3] = temp,b[0],b[1],b[2]

#print(m)

9. 基于对称密码和公钥证书的密钥分发

9.1 基于对称加密的密钥分发

对称加密中，通信双方使用的是相同的密钥且该密钥保密。对通信双方来说，密钥可以通过以下方式传输：

A选择密钥后，通过物理方式传输给B。
第三方选择密钥后，物理传输给A和B。
如果A和B已经在使用一个密钥，可以将新密钥加密后发送给对方，然后双方更新自己的密钥。
如果A和B到可信第三方C有加密连接，C可以在加密连接上传输密钥给A和B。

对于1和2，这两种方案在大范围的密钥交换或者密钥分发时明显不适用；对于3，缺点在于一旦攻击者攻破了某一次用户使用的密钥，那么接下来每一次更换的密钥都会被获取，有潜在风险。对于4，目前广泛采用其变体。

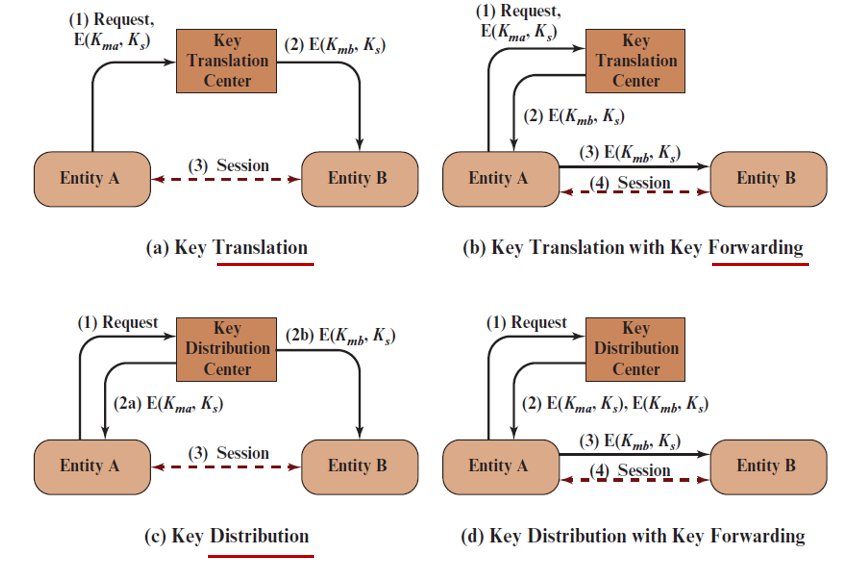
应用密码学

以下为对不同情景的简要分析：

对a，A使用\(K_{ma}\)对生成或者获取的\(K_s\)进行加密后发送给KTC,KTC解密后使用\(K_{mb}\)在加密，把\(K_s\)发送给B。
对b，步骤和a基本相同，不过获得\(E(K_{mb},K_s)\)后，由A转交而不是由KTC发放。
对c，是分发密钥，A发出请求后，KTC为A和B分别分发用于通信的对称会话密钥\(K_s\).
对d，与c类似，不过会话密钥由A转发。

9.2 公钥证书的密钥分发

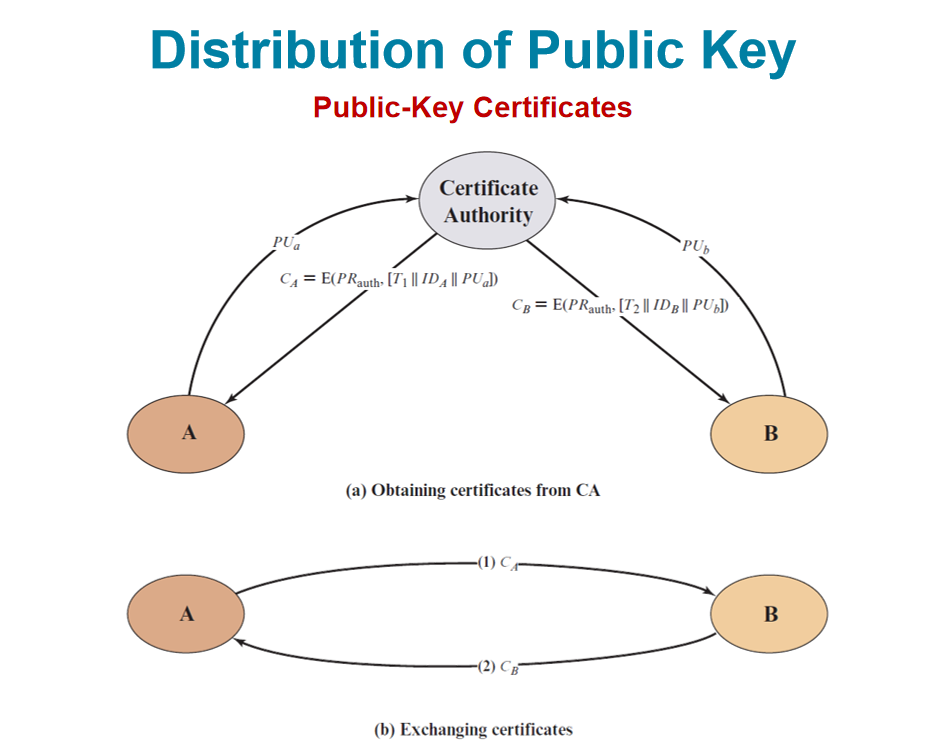
应用密码学

公钥证书方案需要一个公钥证书颁发机构（CA）来运作，大致运行方法如下：

A向CA发送自己的公钥\(PU_a\)，CA使用使用证书管理员的私钥\(PR_{auth}\),对当前时间戳，A的身份标识，以及A的公钥进行加密获得的\(C_A\)就是A的证书。
B收到A的证书后，使用证书管理员的公钥\(PU_{auth}\)对证书进行解密，即可获得A的公钥和身份标识等信息，用于验证通信方是否为A，在发送时，也可以使用\(PU_{auth}\)对证书加密后再发出，能让接收方确认证书确实来自证书管理员。

9.2.1 X.509证书

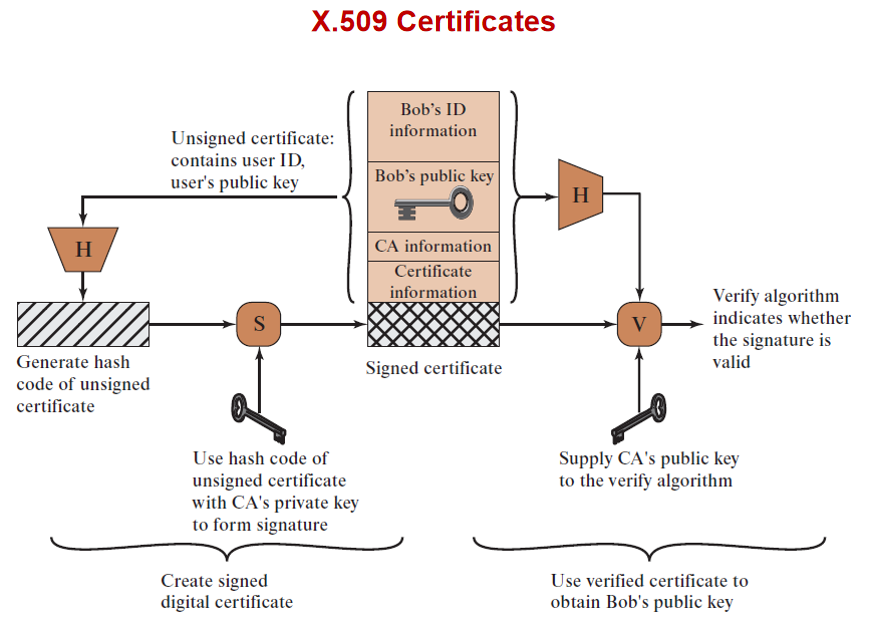
应用密码学

这里的思路和数字签名有些类似（就是上了个签名），先放个传送门：传送门

其实现是对A的证书内容进行Hash加密，然后再使用CA的私钥对哈希值加密后再附加到证书内容后。

验证的时候，先计算获得的证书内容的Hash值，然后将与使用CA公钥解密后的签名进行比对，若一致，可以认为证书有效。

posted on 2023-11-28 21:03 H4RUH1RO 阅读(473) 评论(0) 编辑收藏举报

刷新页面返回顶部

N	\(B_3\)	\(B_2\)	\(B_1\)	\(B_0\)	\(B_0\bigoplus B_1\)	OUTPUT
0	1	0	0	0	0	0
1	0	1	0	0	0	0
2	0	0	1	0	1	0
3	1	0	0	1	1	1
4	1	1	0	0	0	0
5	0	1	1	0	1	0
6	1	0	1	1	0	1
7	0	1	0	1	1	1
8	1	0	1	0	1	0
9	1	1	0	1	1	1
10	1	1	1	0	1	0
11	1	1	1	1	0	1
12	0	1	1	1	0	1
13	0	0	1	1	0	1
14	0	0	0	1	1	1
15	1	0	0	0	0	0

N	\(B_3\)	\(B_2\)	\(B_1\)	\(B_0\)	\(B_0\bigoplus B_1\)	OUTPUT
0	1	0	0	0	0	0
1	0	1	0	0	0	0
2	0	0	1	0	1	0
3	1	0	0	1	1	1
4	1	1	0	0	0	0
5	0	1	1	0	1	0
6	1	0	1	1	0	1
7	0	1	0	1	1	1
8	1	0	1	0	1	0
9	1	1	0	1	1	1
10	1	1	1	0	1	0
11	1	1	1	1	0	1
12	0	1	1	1	0	1
13	0	0	1	1	0	1
14	0	0	0	1	1	1
15	1	0	0	0	0	0

H4RUH1RO