贝叶斯定理在状态估计中应用

1. 贝叶斯定理有什么用？

伟大的英国数学家托马斯·贝叶斯，在1763年发表的一篇论文中，为了解决一个“逆概率”问题，而提出了贝叶斯定理，在此之前，人们已经能计算“正向概率”。

什么是“正向概率”，举个例子，抽奖桶里有10个球，其中2个白球，8个黑球，抽到白球就算你中奖，容易知道中奖概率为0.2。而“逆向概率”就是在不知道桶内球的情况，而是摸出一个球，通过观察这个球的颜色，来预测这个桶里里白色球和黑色球的比例。

**生活中绝大多数决策面临的信息都是不全的，我们手中只有有限的信息需在有限的信息情况下，尽可能做出一个好的预测**

2. 什么是贝叶斯定理

基本公式

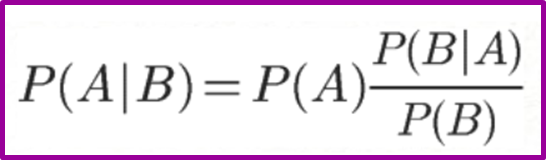
一个栗子
问题：小鹿同学说，他的女神每次看到他的时候都冲他笑，他现在想知道女神是不是喜欢他呢?
基本假设：
（1）记女神喜欢小鹿同学为事件A
（2）记女神经常对小鹿同学笑为事件B
要求解的问题：女神经常对你笑这个事件(B)发生后，女神喜欢你(A)的概率，即P(A|B)

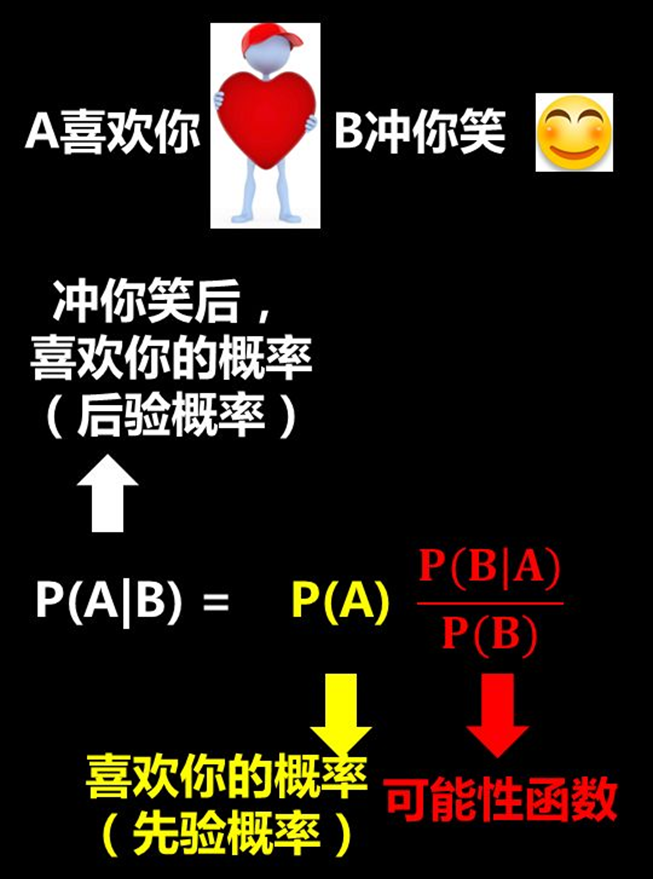
三个概念:

• 先验概率P(A)：在现有的已知条件下，根据经验对事件A的一个主观判断
• 可能性函数P(B|A)/P(B)：利用更新的现有信息来调整之前的先验概率（之前的主观判断），使其更接近其真实概率
  • 若“可能性函数”>1，先验概率被增强，事件A发生的可能性变大
    若“可能性函数”=1，更新的信息无助于判断事件A的可能性
    若“可能性函数”<1，先验概率被削弱，事件A发生的可能性变小
• 后验概率P(A |B)：即为需要求解的问题，利用更新的现有信息来预测出目标问题发生的概率

在此例中，我们猜测女神喜欢与不喜欢小鹿同学的概率为50%，这个主观判断的概率并不是固定，比如小鹿同学之前借了一块橡皮给他的女神，那么我们可以假设P(A)的概率为60%，这里我们还是以50%为例

我们与女神闺蜜交流后，发现女神平时比较高冷，很少对人笑，所以对你有好感的可能性较大（可能性函数大于1），我们假设可能性函数为1.5,最后，后验概率也就是我们需要求解的问题，在此例中，根据50%的先验概率和可能性函数为1.5可以算出，女神冲你笑是喜欢你的概率为75%

3. 什么是状态估计

自动驾驶定位技术的目标是能够准确的获得移动物体在大地坐标系下的一个位姿，实际中由于各种因素的干扰，我们通过传感器获取的位姿是带有一定噪声的，因此定位技术就是要在带有噪声的数据中获得满足误差精度的位姿。

如下图所示，假设我们蒙着眼睛沿着道路走，尽管我们知道自己每一步走了多远。但是随着时间的流逝，我们内心会越来越不安，不确定自己的位置，这里的不确定性大小也就是左图中圆圈的大小，如果中途我们睁开双眼，看看周围的环境，就会使得不确定性变小，自己也会越来越自信朝着目的地前进

在刚刚那个例子中，有两个动作，一个是按照一定长度往前走和睁眼查看周围环境，用数学来描述这个两个过程，就可以得到运动方程和观测方程

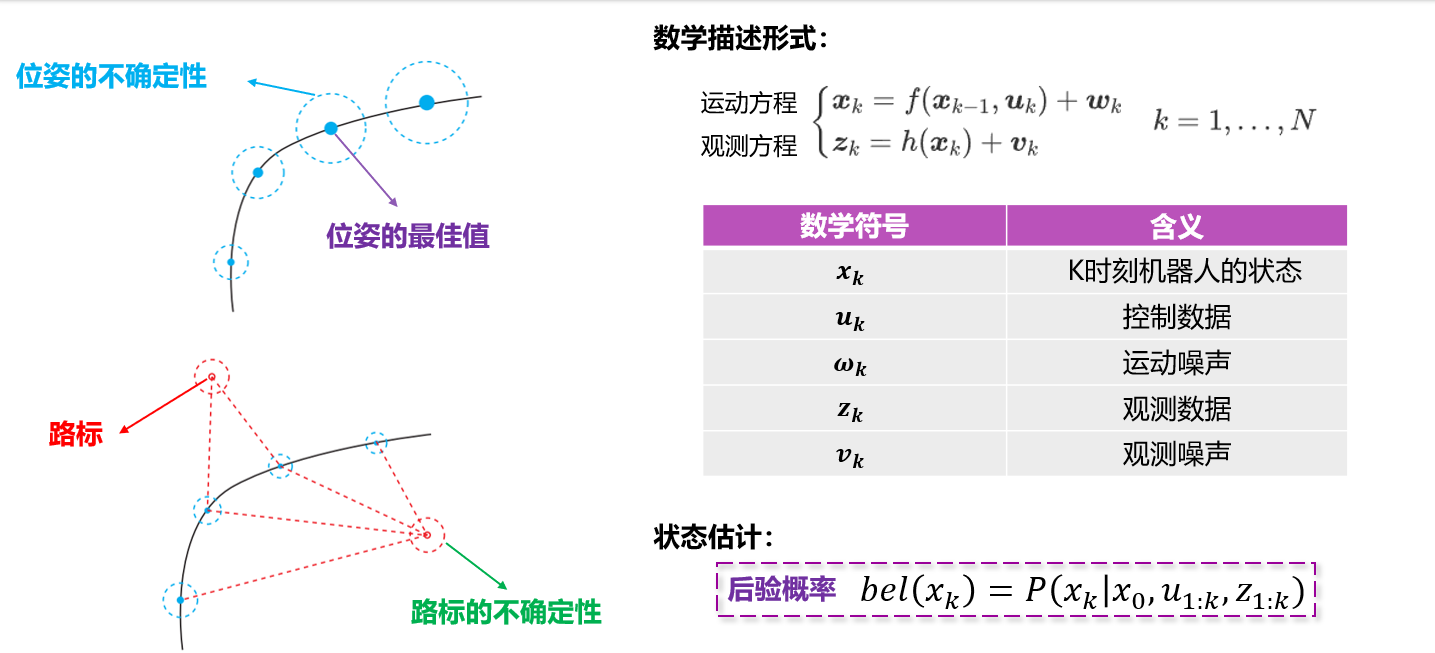
4. 状态估计求解

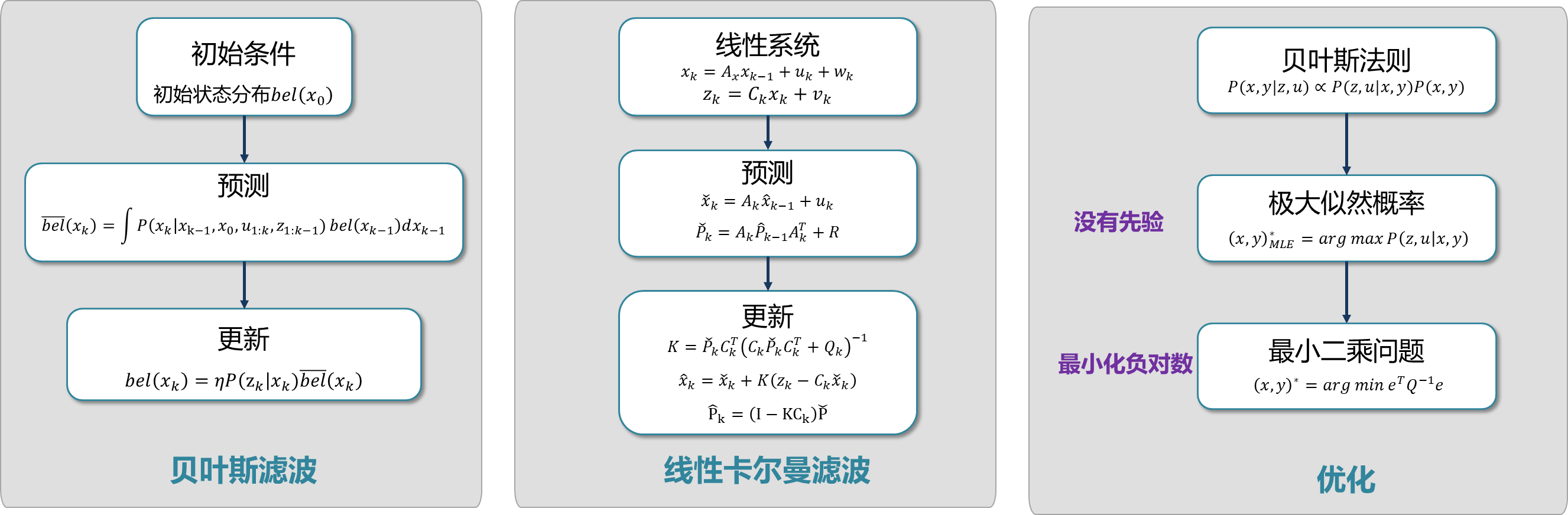
贝叶斯滤波求解状态估计

贝叶斯滤波过程

5.滤波与优化

状态估计的非线性优化求解方法：
给定状态量的初值，通过优化迭代目标函数（预测与观测的差值）求出某时刻的状态量，随着时间的推移，有越来越多的不同时刻的状态量，倘若算力无限前提下，可以每一时刻进行全部状态的优化，但现实是骨感的，需要想办法来控制优化的规模（滑动窗口、共视图）

状态估计的滤波方法：
基于马尔科夫性假设，认为当前时刻的状态只与前一时刻状态有关，因此就权衡上一时刻状态预测、观测误差两者的可信度，来进行当前时刻的状态估计

【参考】
1. 贝叶斯公式的直观理解(先验概率/后验概率)
2.卡尔曼滤波：究竟滤了谁？
3. 贝叶斯定理厉害在哪里？
4. SLAM十四讲--高翔