计算几何
20230721
向量
-
向量的加减,直接
struct Point{ double x,y; Point(double a=0,double b=0){x=a,y=b;} Point operator + (Point A){return Point(x+A.x,y+A.y);} Point operator - (Point A){return Point(x-A.x,y-A.y);} }; -
向量的夹角,记作
-
向量的模长,记作
顾名思义,
代码上可以用点积来实现。
double Length(Point A){return sqrt(Dot(A,A));} -
向量的点积
几何意义:
应用:
若
若
若
double Dot(Point A,Point B){return A.x*B.x+A.y*B.y;} -
向量的叉积
几何意义:以
应用:
若
若
若
两向量所组成的三角形面积为其叉积除以二。
double Cross(Point A,Point B){return A.x*B.y-A.y*B.x;} -
向量的旋转
将向量
-
向量的极角
与x轴正半轴的夹角,
-
点与线的距离
与直线:面积除以底边长。
与射线或线段:判断垂足是否在线段上(用点积判断夹角)。
垂足:点积除以模长得到投影长度,用投影长度之比来算。
//求m到线段ab的最短距离的点 vec x=m-a,y=m-b,z=b-a; if(x==z){ans=0.0,res=m;return;} if(cmp(Dot(x,z))<0) tmp=a;//在a时取到最小 else if(cmp(Dot(y,z))>0) tmp=b; else{ xx1=Dot(x,z)/Lenth(z); xx2=-1.0*Dot(y,z)/Lenth(z); tmp=a+z*(xx1/(xx1+xx2));//求垂足 } if(cmp(Lenth(tmp-m)-Lenth(m-res))<0) res=tmp; -
线与线的交点
设两条直线
首先需要排除平行或重合的情况,
通过面积法计算出
从而求出
即使
vec sec(lne x,lne y){ double len1=cro(y.a-x.a,y.b-x.a),len2=cro(y.a-x.b,y.b-x.b); return x.b+(x.a-x.b)*(len2/(len2-len1)); }应用:
线段与直线的交点:判断交点是否在线段上。
线段与线段的交点:判断交点是否在线段上。
判断 两条线段是否相交:可以直接判断两直线是否跨立,即
就只需判断
判断
UVA10263 Railway-点与线
点与线的距离。
求点到线段的距离即可。
注意误差问题很重要!
cmp函数很重要!!!
#include <bits/stdc++.h>
using namespace std;
const double eps=1e-5;
int n;
double ans=0,x,dis,xx1,xx2;
struct vec{
double x,y;
vec(double a=0,double b=0){x=a,y=b;}
vec operator +(const vec &a) const{return vec(x+a.x,y+a.y);}
vec operator -(const vec &a) const{return vec(x-a.x,y-a.y);}
vec operator *(double k)const{return vec(k*x,k*y);}
bool operator ==(const vec &a)const{return (x==a.x&&y==a.y)?1:0;}
}m,st,a,b,tmp,res;
double Dot(vec a,vec b){return a.x*b.x+a.y*b.y;}
double Cross(vec a,vec b){return a.x*b.y-b.x*a.y;}
double Lenth(vec a){return sqrt(Dot(a,a));}
int cmp(double p){return p<-eps?-1:(p>eps?1:0);}
void solve(vec m,vec a,vec b){
vec x=m-a,y=m-b,z=b-a;
if(x==z){ans=0.0,res=m;return;}
if(cmp(Dot(x,z))<0) tmp=a;
else if(cmp(Dot(y,z))>0) tmp=b;
else{
xx1=Dot(x,z)/Lenth(z);
xx2=-1.0*Dot(y,z)/Lenth(z);
tmp=a+z*(xx1/(xx1+xx2));
}
if(cmp(Lenth(tmp-m)-Lenth(m-res))<0) res=tmp;
}
int main(){
/*2023.7.21 H_W_Y UVA10263 Railway 计算几何*/
while(scanf("%lf",&m.x)!=EOF){
ans=(double)1000000000;
scanf("%lf%d%lf%lf",&m.y,&n,&st.x,&st.y);a=st;
for(int i=2;i<=n+1;i++){
scanf("%lf%lf",&b.x,&b.y);
solve(m,a,b);a=b;
}
solve(m,st,a);
printf("%.4lf\n%.4lf\n",res.x,res.y);
}
return 0;
}
P4468 [SCOI2007] 折纸-点与线
一个左下角为
, 右上角为 的正方形纸片, 连续 次关于一条给定直线翻折,
将该直线的右侧翻到左侧,操作完后次询问某个点上有多少层纸, 。
考虑对于每一个点,
我们倒着递推每一条直线,
如果一个点在某条直线的右侧,那么就返回0。
否则它为它自己在之前的层数加上对称点之前的层数,
和上一道题找垂足的方法一致。
我们把过程转移到一个dfs里面即可。
时间复杂度
由于
所以这样是可以过的。
注意细节!在枚举完所有直线后判断1,0的细节。。。
#include <bits/stdc++.h>
using namespace std;
const double eps=1e-6;
int n,m;
struct vec{
double x,y;
vec(double a=0,double b=0){x=a,y=b;}
vec operator +(const vec &a)const{return vec(x+a.x,y+a.y);}
vec operator -(const vec &a)const{return vec(x-a.x,y-a.y);}
vec operator *(double k)const{return vec(k*x,k*y);}
bool operator ==(const vec &a)const{return (a.x==x&&a.y==y)?1:0;}
}x;
double Dot(vec a,vec b){return a.x*b.x+a.y*b.y;}
double Cro(vec a,vec b){return a.x*b.y-b.x*a.y;}
double Len(vec a){return sqrt(Dot(a,a));}
int cmp(double p){return p<-eps?-1:(p>eps)?1:0;}
struct lne{
vec a,b;
}l[10];
vec opp(vec p,lne l){
vec x=p-l.a,y=p-l.b,z=l.b-l.a;
double len1=Dot(x,z)/Len(z);
double len2=-1.0*Dot(y,z)/Len(z);
x=l.a+z*(len1/(len1+len2));
return x*2.0-p;
}
int dfs(int i,vec x){
if(i==0) return (cmp(x.x)>0&&cmp(x.x-100.0)<0&&cmp(x.y)>0&&cmp(x.y-100.0)<0)?1:0;
if(cmp(Cro(l[i].a-x,l[i].b-x))<=0||l[i].a-x==x-l[i].b) return 0;
return dfs(i-1,x)+dfs(i-1,opp(x,l[i]));
}
int main(){
/*2023.7.21 H_W_Y P4468 [SCOI2007] 折纸 计算几何*/
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lf%lf%lf%lf",&l[i].a.x,&l[i].a.y,&l[i].b.x,&l[i].b.y);
scanf("%d",&m);
for(int i=1;i<=m;i++){
scanf("%lf%lf",&x.x,&x.y);
printf("%d\n",dfs(n,x));
}
return 0;
}
P4529 [SCOI2003] 切割多边形-线与线
我们希望通过切割得到一个凸
边形 (坐标已给出)。 一开始的时候,你有一个
的矩形,即它的四角的坐标分别为 。每次,你可以选择一条直线把当前图形切割成两部分,保留其中一个部分(另一部分扔掉),切割线的长度为此直线在多边形内部的部分的长度。求出最短的切割线总长度。
。
第一次自己做出来一道黑题耶(好像也没有想象那么难)
由于我们发现
所以考虑直接爆搜。
我们用dfs枚举所有的切割顺序,
在递归过程中统计答案,直到每次统计完所有的线段就记录答案即可。
现在来考虑如何记录答案,
不难想到要用到计算几何的知识。
我们只需要在已经加入的切割直线中与当前的直线
找到把
再记录此时线段
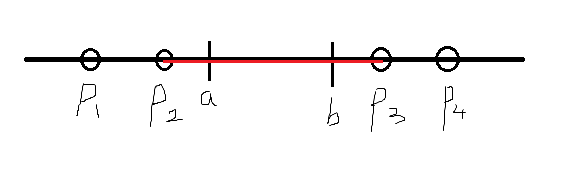
如图,
也就是多边形的顶点。
我们希望找到的就是图中的
这样这条线段的贡献就是
也就是红色的一段。
现在再来考虑如何找交点,
和上面讲的一样,用面积比例和向量完成即可。
代码细节还是挺多的。
#include <bits/stdc++.h>
using namespace std;
const double eps=1e-4;
int p,cnt=0;
double n,m,ans=1.0*1e9;
bool vis[15];
struct vec{
double x,y;
vec(double a=0,double b=0){x=a,y=b;}
vec operator +(const vec &a)const {return vec(x+a.x,y+a.y);}
vec operator -(const vec &a)const {return vec(x-a.x,y-a.y);}
vec operator *(double k)const {return vec(x*k,y*k);}
bool operator ==(const vec &a){return (x==a.x&&y==a.y)?1:0;}
};
double dts(vec a,vec b){return a.x*b.x+a.y*b.y;}
double cro(vec a,vec b){return a.x*b.y-b.x*a.y;}
double len(vec a){return sqrt(dts(a,a));}
int cmp(double a){return a<-eps?-1:(a>eps?1:0);}
struct lne{
vec a,b;
}l[15],lst[15];
vec sec(lne x,lne y){
double len1=cro(y.a-x.a,y.b-x.a),len2=cro(y.a-x.b,y.b-x.b);
return x.b+(x.a-x.b)*(len2/(len2-len1));
}
double vecdis(lne x){
vec ll,rr;rr.x=(double)505;ll.x=(double)-1;
for(int i=1;i<=cnt;i++){
if(cmp(cro(x.a-x.b,lst[i].a-lst[i].b))==0) continue;
vec tmp=sec(x,lst[i]);
if(cmp(tmp.x-n)>0||cmp(tmp.x)<0||cmp(tmp.y-m)>0||cmp(tmp.y)<0) continue;
if(cmp(tmp.x-x.a.x)>=0)
if(cmp(rr.x-tmp.x)>0) rr=tmp;
if(cmp(tmp.x-x.b.x)<=0)
if(cmp(ll.x-tmp.x)<0) ll=tmp;
if(cmp(tmp.x-x.a.x)==0&&cmp(tmp.x-x.b.x)==0){//两个同时满足
if(cmp(tmp.y-x.a.y)>0) rr=tmp;
else if(cmp(tmp.y-x.b.y)<0) ll=tmp;
}
}
return len(rr-ll);
}
void dfs(int stp,double res){
if(stp==p){ans=min(ans,res);return;}
for(int i=1;i<=p;i++){
if(vis[i]) continue;
vis[i]=true;
double dis=vecdis(l[i]);
lst[++cnt]=l[i];
dfs(stp+1,res+dis);
vis[i]=false;cnt--;
}
}
int main(){
/*2023.7.22 H_W_Y P4529 [SCOI2003] 切割多边形 计算几何*/
scanf("%lf%lf%d",&n,&m,&p);
lst[1]=(lne){vec(0,0),vec(0,m)};
lst[2]=(lne){vec(n,m),vec(0,m)};
lst[3]=(lne){vec(n,0),vec(0,0)};
lst[4]=(lne){vec(n,0),vec(n,m)};cnt=4;
for(int i=1;i<=p;i++) scanf("%lf%lf",&l[i].b.x,&l[i].b.y),l[i].a=l[i-1].b;
l[1].a=l[p].b;
for(int i=1;i<=p;i++){
if(cmp(l[i].a.x-l[i].b.x)<0) swap(l[i].a,l[i].b);
else if(cmp(l[i].a.x-l[i].b.x)==0){
if(cmp(l[i].a.y-l[i].b.y)<0) swap(l[i].a,l[i].b);
}
}
dfs(0,0.0);
printf("%.3lf\n",ans);
return 0;
}
多边形
一般只考虑简单多边形(不自交),
存储方法:把顶点依次存储,一般逆时针。
-
凸多边形?
即判断每一条折线的拐向是否相同,
而对于折线
如果其
-
点与多边形的关系
特判点是否在多边形的边上或者点上。
射线法:
从点出发,做一条平行于x轴的射线,
统计与多边形的交点数,
如果有奇数个交点,即在多边形内部。
偶数个交点,则在多边形外部。
注意:如果交点在顶点,那么规定交在下端点不视为相交。
-
多边形面积
依次枚举两个相邻的端点,用叉积算他们与原点组成的面积,
注意需要保留符号,最后要除以2。

圆
存储方法:圆心+半径。
-
点与圆的关系
判断点到圆心的距离与圆的半径的关系。
-
线与圆的关系(交点)
先判断圆心到直线的距离,如果该距离大于半径,
那么线与圆没有交点。
否则,先求出
再用勾股定理求出
进而得到

lne sec_cir(lne x,vec a,double r){//求线与圆的交点 cnt=0;double d=dis(a,x); vec tmp,res1,res2; if(cmp(d-r)>0) return lne(0,0,0,0); if(cmp(d-r)==0){ cnt=1; tmp=dis_point(a,x); return lne(tmp.x,tmp.y,0,0); } cnt=2; tmp=dis_point(a,x); double l=sqrt(r*r-d*d); res1=tmp+(x.a-x.b)*(l/len(x.a-x.b)); res2=tmp-(x.a-x.b)*(l/len(x.a-x.b)); return lne(res1.x,res1.y,res2.x,res2.y); }
-
圆与圆的交点
先求出圆心距,从而可以排除外离和内含的情况。
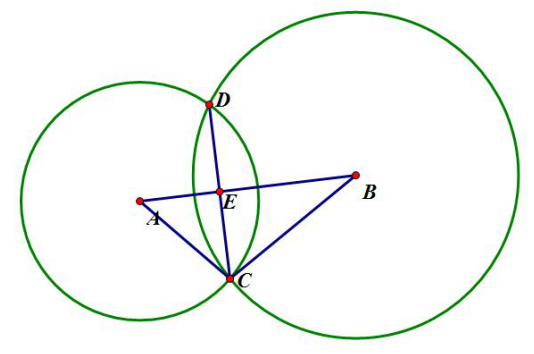
如图,其中
再用余弦定理求出
这样就知道了
再通过勾股定理求线与圆的交点得到
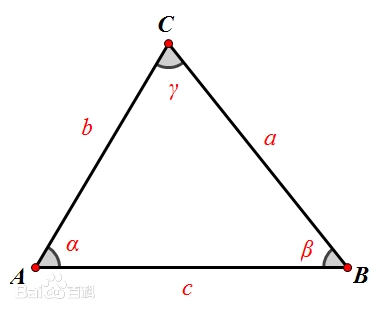
余弦定理:
lne cir_cir(vec a,double r1,vec b,double r2){//求圆与圆的交点 cnt=0;double d=len(a-b); vec ans,p;lne res; if(cmp(d-r1-r2)>0||cmp(d+r1-r2)<0||cmp(d+r2-r1)<0) return lne(0,0,0,0); if(cmp(d-r1-r2)==0){ cnt=1;ans=a+(b-a)*(r1/(r1+r2)); return lne(ans.x,ans.y,0,0); } if(cmp(d+r1-r2)==0){ cnt=1;ans=b+(a-b)*(r2/(r2-r1)); return lne(ans.x,ans.y,0,0); } if(cmp(d+r2-r1)==0){ cnt=1;ans=a+(b-a)*(r1/(r1-r2)); return lne(ans.x,ans.y,0,0); } cnt=2; double c=(d*d+r1*r1-r2*r2)/(2.0*d*r1),l;//余弦定理求cos l=c*r1; ans=b-a; p=a+(ans)*(l/len(ans)); swap(ans.x,ans.y); ans.x=-1.0*ans.x; res.a=p+ans*(sqrt(r1*r1-l*l)/len(ans)); res.b=p-ans*(sqrt(r1*r1-l*l)/len(ans)); return res; }
UVA12304 2D Geometry 110 in 1!
UVA12304 2D Geometry 110 in 1!
这是一道六合一题目:
- 求三角形外接圆。
- 求三角形内切圆。
- 求给定点关于圆的切线。
- 给定圆上一点、半径,以及该圆的一条切线,求圆心。
- 给定圆的两条切线以及半径,求圆心。
- 给定两圆以及一个常量 r,求所有半径为 r 且与两圆都相切的圆的圆心。
-
就是求三条边的中垂线的交点。
-
就是求三条角平分线的交点。
两个相同向量的角平分线:
可以先将两个向量转化为长度相同,即
这样角平分线就是
-
可以运用勾股定理求出
从而用向量的旋转公式算出答案的两个向量。
再通过向量的极角算出答案。
注意最后极角度数要
/3.14159265358979 * 180。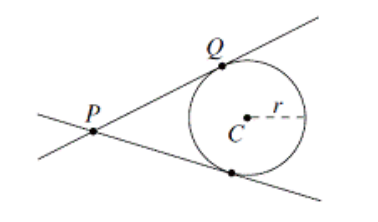
-
由于
所以圆形一定是在以
而又给出了一条切线,
那么圆心一定是在距离该切线为
这样分别求这个圆与两条线的交点即可。
最多有四个答案。
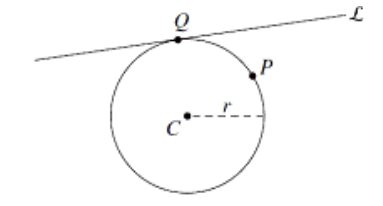
-
和4一样的方法,
只不过这次把那个圆又换成了两条线。
分别求交点即可,
注意也有四种答案。
-
由于圆心到圆上点的距离都为
我们考虑把这两个圆都向外膨胀
也就是半径分别加
在计算此时两个圆的交点即可。
最多有两种答案。
注意后面几种答案数量不定的都还是需要特殊判断一下。
#include <bits/stdc++.h>
using namespace std;
#define long double double
const double eps=1e-8;
double r;
int cnt=0;
struct vec{
double x,y;
vec(double a=0,double b=0){x=a,y=b;}
vec operator +(const vec &a) const{return vec(x+a.x,y+a.y);}
vec operator -(const vec &a) const{return vec(x-a.x,y-a.y);}
vec operator *(const double k) const{return vec(x*k,y*k);}
vec operator /(const double k) const{return vec(x/k,y/k);}
}a,b,c;
string s;
struct lne{
vec a,b;
lne(double x=0,double y=0,double xx=0,double yy=0){a.x=x,a.y=y;b.x=xx;b.y=yy;}
}l1,l2;
double dts(vec a,vec b){return a.x*b.x+a.y*b.y;}//点积
double cro(vec a,vec b){return a.x*b.y-a.y*b.x;}//叉积
double len(vec a){return sqrt(dts(a,a));} //模长
vec sec(lne x,lne y){//求线与线的交点
double len1=cro(y.a-x.a,y.b-x.a),len2=cro(y.a-x.b,y.b-x.b);
return x.b+(x.a-x.b)*(len2/(len2-len1));
}
double dis(vec a,lne l){//求点到线的距离
vec x=a-l.a,y=a-l.b,z=l.b-l.a;
return fabs(cro(x,y)/len(z));
}
vec dis_point(vec a,lne l){//求点到线的垂足
vec x=a-l.a,y=a-l.b,z=l.b-l.a,tmp;
double xx1=dts(x,z)/len(z);
double xx2=-1.0*dts(y,z)/len(z);
tmp=l.a+z*(xx1/(xx1+xx2));
return tmp;
}
int cmp(double k){//比大小
return k<-eps?-1:(k>eps?1:0);
}
bool cmp2(vec a,vec b){//排序
if(cmp(a.x-b.x)!=0) return cmp(a.x-b.x)<0;
return cmp(a.y-b.y)<0;
}
lne sec_cir(lne x,vec a,double r){//求线与圆的交点
cnt=0;double d=dis(a,x);
vec tmp,res1,res2;
if(cmp(d-r)>0) return lne(0,0,0,0);
if(cmp(d-r)==0){
cnt=1;
tmp=dis_point(a,x);
return lne(tmp.x,tmp.y,0,0);
}
cnt=2;
tmp=dis_point(a,x);
double l=sqrt(r*r-d*d);
res1=tmp+(x.a-x.b)*(l/len(x.a-x.b));
res2=tmp-(x.a-x.b)*(l/len(x.a-x.b));
return lne(res1.x,res1.y,res2.x,res2.y);
}
lne cir_cir(vec a,double r1,vec b,double r2){//求圆与圆的交点
cnt=0;double d=len(a-b);
vec ans,p;lne res;
if(cmp(d-r1-r2)>0||cmp(d+r1-r2)<0||cmp(d+r2-r1)<0) return lne(0,0,0,0);
if(cmp(d-r1-r2)==0){
cnt=1;ans=a+(b-a)*(r1/(r1+r2));
return lne(ans.x,ans.y,0,0);
}
if(cmp(d+r1-r2)==0){
cnt=1;ans=b+(a-b)*(r2/(r2-r1));
return lne(ans.x,ans.y,0,0);
}
if(cmp(d+r2-r1)==0){
cnt=1;ans=a+(b-a)*(r1/(r1-r2));
return lne(ans.x,ans.y,0,0);
}
cnt=2;
double c=(d*d+r1*r1-r2*r2)/(2.0*d*r1),l;//余弦定理求cos
l=c*r1;
ans=b-a;
p=a+(ans)*(l/len(ans));
swap(ans.x,ans.y);
ans.x=-1.0*ans.x;
res.a=p+ans*(sqrt(r1*r1-l*l)/len(ans));
res.b=p-ans*(sqrt(r1*r1-l*l)/len(ans));
return res;
}
void solve_1(){//1.求三角形的外接圆 -> 三边垂直平分线的交点
scanf("%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y);
l1.a=(a+b)/2;l2.a=(a+c)/2;
l1.b=a-b;swap(l1.b.x,l1.b.y);l1.b.x=-l1.b.x;l1.b=l1.a+l1.b;
l2.b=a-c;swap(l2.b.x,l2.b.y);l2.b.x=-l2.b.x;l2.b=l2.a+l2.b;
vec ans=sec(l1,l2);
printf("(%.6lf,%.6lf,%.6lf)\n",ans.x,ans.y,len(ans-a));
}
void solve_2(){//2.求三角形的内切圆 -> 角平分线的交点
scanf("%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&b.x,&b.y,&c.x,&c.y);
l1.a=a;l2.a=b;
vec x=c-a,y=b-a;
x=x*(len(y)/len(x));l1.b=x+y;l1.b=l1.a+l1.b;
x=c-b,y=a-b;
x=x*(len(y)/len(x));l2.b=x+y;l2.b=l2.a+l2.b;
vec ans=sec(l1,l2);
printf("(%.6lf,%.6lf,%.6lf)\n",ans.x,ans.y,dis(ans,lne(a.x,a.y,b.x,b.y)));
}
void solve_3(){//3.求给定点关于圆的切线
scanf("%lf%lf%lf%lf%lf",&a.x,&a.y,&r,&b.x,&b.y);
vec p,p1,p2;
double ans1,ans2,ang;
if(cmp(len(b-a)-r)<0){printf("[]\n");return;}
if(cmp(len(b-a)-r)==0){
p=a-b;swap(p.x,p.y);p.x=-p.y;
ans1=atan2(p.y,p.x)/3.14159265358979*180;
if(cmp(ans1)<0) ans1+=1.0*180;
if(cmp(ans1-180)==0) ans1=0;
printf("[%.6lf]\n",ans1);
return;
}
p=a-b;
double l=sqrt(dts(p,p)-r*r);
ang=acos(l/len(p));
p1=vec(p.x*cos(ang)+p.y*sin(ang),-1.0*p.x*sin(ang)+p.y*cos(ang));
ans1=atan2(p1.y,p1.x)/3.14159265358979*180;
if(cmp(ans1)<0) ans1+=1.0*180;
if(cmp(ans1-180)==0) ans1=0;
ang=-1.0*ang;
p2=vec(p.x*cos(ang)+p.y*sin(ang),-1.0*p.x*sin(ang)+p.y*cos(ang));
ans2=atan2(p2.y,p2.x)/3.14159265358979*180;
if(cmp(ans2)<0) ans2+=1.0*180;
if(cmp(ans2-180)==0) ans2=0;
if(cmp(ans1-ans2)>0) swap(ans1,ans2);
printf("[%.6lf,%.6lf]\n",ans1,ans2);
}
void solve_4(){//4.给定圆上一点、半径,以及该圆的一条切线,求圆心
lne l,p;int res=0;
scanf("%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&l.a.x,&l.a.y,&l.b.x,&l.b.y,&r);
vec x=vec(l.a.y-l.b.y,l.b.x-l.a.x),pri[5];
p.a=l.a+x*(r/len(x));p.b=l.a-x*(r/len(x));
l1.a=p.a;l2.a=p.b;
l1.b=p.a+(l.a-l.b);l2.b=p.b+(l.a-l.b);
lne ans=sec_cir(l1,a,r);
res=cnt;
if(cnt==1) pri[1]=ans.a;
if(cnt==2) pri[1]=ans.a,pri[2]=ans.b;
ans=sec_cir(l2,a,r);
if(cnt==1) pri[res+1]=ans.a;
if(cnt==2) pri[res+1]=ans.a,pri[res+2]=ans.b;
res+=cnt;
if(res==0){printf("[]\n");return;}
sort(pri+1,pri+res+1,cmp2);
printf("[");
for(int i=1;i<=res;i++){
printf("(%.6lf,%.6lf)",pri[i].x,pri[i].y);
if(i!=res) printf(",");
}
printf("]\n");
}
void solve_5(){//5.给定圆的两条切线以及半径,求圆心
lne l3,l4,l,ll,p;
scanf("%lf%lf%lf%lf%lf%lf%lf%lf%lf",&l.a.x,&l.a.y,&l.b.x,&l.b.y,&ll.a.x,&ll.a.y,&ll.b.x,&ll.b.y,&r);
vec x=vec(l.a.y-l.b.y,l.b.x-l.a.x),pri[5];
p.a=l.a+x*(r/len(x));p.b=l.a-x*(r/len(x));
l1.a=p.a;l2.a=p.b;
l1.b=p.a+(l.a-l.b);l2.b=p.b+(l.a-l.b);
x=vec(ll.a.y-ll.b.y,ll.b.x-ll.a.x);
p.a=ll.a+x*(r/len(x));p.b=ll.a-x*(r/len(x));
l3.a=p.a;l4.a=p.b;
l3.b=p.a+(ll.a-ll.b);l4.b=p.b+(ll.a-ll.b);
pri[1]=sec(l1,l3);pri[2]=sec(l1,l4);
pri[3]=sec(l2,l3);pri[4]=sec(l2,l4);
sort(pri+1,pri+5,cmp2);
printf("[");
for(int i=1;i<=4;i++){
printf("(%.6lf,%.6lf)",pri[i].x,pri[i].y);
if(i!=4) printf(",");
}
printf("]\n");
}
void solve_6(){//6.给定两圆以及一个常量 r,求所有半径为 r 且与两圆都相切的圆的圆心
double r1,r2;
scanf("%lf%lf%lf%lf%lf%lf%lf",&a.x,&a.y,&r1,&b.x,&b.y,&r2,&r);
r1+=r;r2+=r;
lne ans=cir_cir(a,r1,b,r2);
if(cnt==0){printf("[]\n");return;}
if(cnt==1){printf("[(%.6lf,%.6lf)]\n",ans.a.x,ans.a.y);return;}
if(cmp(ans.a.x-ans.b.x)>0) swap(ans.a,ans.b);
printf("[(%.6lf,%.6lf),(%.6lf,%.6lf)]\n",ans.a.x,ans.a.y,ans.b.x,ans.b.y);
}
int main(){
/*2023.7.25 H_W_Y UVA12304 2D Geometry 110 in 1! 计算几何*/
while(cin>>s){
if(s=="CircumscribedCircle") solve_1();//1.求三角形的外接圆
if(s=="InscribedCircle") solve_2();//2.求三角形的内切圆
if(s=="TangentLineThroughPoint") solve_3();//3.求给定点关于圆的切线
if(s=="CircleThroughAPointAndTangentToALineWithRadius") solve_4();//4.给定圆上一点、半径,以及该圆的一条切线,求圆心
if(s=="CircleTangentToTwoLinesWithRadius") solve_5();//5.给定圆的两条切线以及半径,求圆心
if(s=="CircleTangentToTwoDisjointCirclesWithRadius") solve_6();//6.给定两圆以及一个常量 r,求所有半径为 r 且与两圆都相切的圆的圆心
}
return 0;
}
凸包
P2742 [USACO5.1] 圈奶牛Fencing the Cows /【模板】二维凸包
凸包模板。
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,tp=0;
struct Point{
double x,y;
Point(double a=0,double b=0){x=a,y=b;}
Point operator + (Point A){return Point(x+A.x,y+A.y);}
Point operator - (Point A){return Point(x-A.x,y-A.y);}
}a[maxn],st[maxn];
double Dot(Point A,Point B){return A.x*B.x+A.y*B.y;}
double Cross(Point A,Point B){return A.x*B.y-A.y*B.x;}
double Length(Point A){return sqrt(Dot(A,A));}
bool cmp1(Point A,Point B){
if(A.x!=B.x) return A.x<B.x;
return A.y<B.y;
}
bool cmp2(Point A,Point B){
double des=Cross(A-a[1],B-a[1]);
if(des!=0) return des>0;
return Length(A-a[1])<Length(B-a[1]);
}
int main(){
/*2023.2.6 hewanying P2742 圈奶牛 凸包*/
scanf("%d",&n);tp=0;
for(int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
if(n==1){printf("0.00\n");return 0;}
if(n==2){printf("%.2f\n",fabs(Length(a[1]-a[2])));return 0;}
sort(a+1,a+n+1,cmp1);
sort(a+2,a+n+1,cmp2);
st[++tp]=a[1];st[++tp]=a[2];st[++tp]=a[3];
for(int i=4;i<=n;i++){
while(tp>=2){
double des=Cross(st[tp]-st[tp-1],a[i]-st[tp]);
if(des<=0) tp--;
else break;
}
st[++tp]=a[i];
}
double s=0;
for(int i=1;i<=tp;i++) s+=Length(st[i%tp+1]-st[i]);
printf("%.2f\n",s);
return 0;
}
闵可夫斯基和
两个图形的 Minkovski 和被定义为
而一下的内容只讨论一下两个凸包的 Minkovski 和。
首先容易发现,如果我们把这两凸包画出来,很容易可以得到他们闵可夫斯基和的表述:(图是盗的)
我们发现这一定也是一个凸包,并且上面的每一条边都还是之前两个凸包上面的边组成的,
所以求它是容易的,我们直接用类似于归并排序的方法求即可。
void minkovski(){
for(int i=1;i<n;i++) a[i]=s[i+1]-s[i];a[n]=s[1]-s[n];
for(int i=1;i<m;i++) b[i]=h[i+1]-h[i];b[m]=h[1]-h[m];
tot=1;G[tot]=s[1]+h[1];
int p1=1,p2=1;
while(p1<=n&&p2<=m) ++tot,G[tot]=G[tot-1]+(a[p1]*b[p2]>=0?a[p1++]:b[p2++]);
while(p1<=n) ++tot,G[tot]=G[tot-1]+a[p1++];
while(p2<=m) ++tot,G[tot]=G[tot-1]+b[p2++];
}
而在求完之后需要再跑一次凸包,因为有可能出现三点共线的情况,
这样我们就做完了。
P4557 [JSOI2018] 战争 - Minkovski
给定两个凸包
, 次询问,每次给出一个向量 ,问 平移向量 后, 和 是否还有交集。
。
问题可以被转化成是否有交集,
于是我们可以列出下面的式子,如果有交:
转化一下:
发现这个东西很想 Minkovski 和,
于是我们把
而最后一步只需要判断一下一个点是否在凸包内,这是好判断的,
直接按照极角排序之后二分一下就可以了。
#include <bits/stdc++.h>
using namespace std;
#define db double
const int N=1e5+5;
int n,m,q,tot=0;
struct vec{db x,y;}a[N],b[N],s[N],h[N],A[N],G[N],d,st;
vec operator +(vec a,vec b){return (vec){a.x+b.x,a.y+b.y};}
vec operator -(vec a,vec b){return (vec){a.x-b.x,a.y-b.y};}
db operator *(vec a,vec b){return a.x*b.y-a.y*b.x;}
db operator &(vec a,vec b){return a.x*b.x+a.y*b.y;}
db cro(vec a,vec b,vec c){return (b-a)*(c-a);}
db len(vec a){return sqrt(a&a);}
bool cmp(vec a,vec b){return (a.x==b.x)?a.y<b.y:a.x<b.x;}
bool cmp2(vec a,vec b){return a*b>0||(a*b==0&&len(a)<len(b));}
void convex(vec *s,vec *p,int &n){
int cnt=0;
sort(p+1,p+n+1,cmp);
s[++cnt]=p[1];
for(int i=2;i<=n;i++){
while(cnt>1&&cro(s[cnt-1],s[cnt],p[i])<=0) --cnt;
s[++cnt]=p[i];
}
int t=cnt;
for(int i=n-1;i>=1;i--){
while(cnt>t&&cro(s[cnt-1],s[cnt],p[i])<=0) --cnt;
s[++cnt]=p[i];
}
n=--cnt;
}
void minkovski(){
for(int i=1;i<n;i++) a[i]=s[i+1]-s[i];a[n]=s[1]-s[n];
for(int i=1;i<m;i++) b[i]=h[i+1]-h[i];b[m]=h[1]-h[m];
tot=1;G[tot]=s[1]+h[1];
int p1=1,p2=1;
while(p1<=n&&p2<=m) ++tot,G[tot]=G[tot-1]+(a[p1]*b[p2]>=0?a[p1++]:b[p2++]);
while(p1<=n) ++tot,G[tot]=G[tot-1]+a[p1++];
while(p2<=m) ++tot,G[tot]=G[tot-1]+b[p2++];
}
bool chk(vec a){
if(a*A[1]>0||A[tot]*a>0) return false;
int pos=lower_bound(A+1,A+tot+1,a,cmp2)-A-1;
return (a-A[pos])*(A[pos%tot+1]-A[pos])<=0;
}
int main(){
/*2023.12.30 H_W_Y P4557 [JSOI2018] 战争 Minkovski*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>q;
for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
for(int i=1;i<=m;i++) cin>>b[i].x>>b[i].y,b[i].x=-b[i].x,b[i].y=-b[i].y;
convex(s,a,n);convex(h,b,m);
minkovski();
convex(A,G,tot);
st=A[1];
for(int i=1;i<=tot;i++) A[i]=A[i]-st;
while(q--){
cin>>d.x>>d.y;
cout<<chk(d-st)<<'\n';
}
return 0;
}
本文作者:H_W_Y
本文链接:https://www.cnblogs.com/H-W-Y/p/geo.html
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步