Data Structure 1
非 lxl 的 DS
不会线性代数,只能来写 DS 了。
20231226-
没有逻辑,直接放例题。
P1527 矩阵乘法 - 整体二分
给你一个 \(n \times n\) 的矩阵,不用算矩阵乘法,但是每次询问一个子矩形的第 \(k\) 小数。
\(1 \leq n \leq 500\),\(1 \leq q \leq 6 \times 10^4\),\(0 \leq a_{i, j} \leq 10^9\)。
第 \(k\) 小的数,很容易想到去二分。
但是对于每一个询问都去二分是肯定不现实的,
于是我们考虑离线下来 整体二分。
每次二分到一个值 \(x\),
我们把 \(\le x\) 的位置染色,判断这个区间内的那些询问是合法的,于是依次往下分治下去。
这样用二维树状数组就可以做到 \(n \log^2 n \log q\),足以通过。
#include <bits/stdc++.h>
using namespace std;
const int N=505,M=6e4+5;
int n,m,id[M],ans[M],t1[M],t2[M],cur[M];
struct node{
int x,y,v;
bool operator <(const node &rhs) const{return v<rhs.v;}
}a[N*N];
struct Qry{int x1,x2,y1,y2,k;}q[M];
struct BIT{
int c[N][N];
void init(){memset(c,0,sizeof(c));}
int lowbit(int i){return i&(-i);}
void upd(int x,int y,int v){
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=n;j+=lowbit(j))
c[i][j]+=v;
}
int qry(int x,int y){
int res=0;
for(int i=x;i>=1;i-=lowbit(i))
for(int j=y;j>=1;j-=lowbit(j))
res+=c[i][j];
return res;
}
int find(int x1,int y1,int x2,int y2){
return qry(x2,y2)-qry(x1-1,y2)-qry(x2,y1-1)+qry(x1-1,y1-1);
}
}t;
int qry(Qry nw){return t.find(nw.x1,nw.y1,nw.x2,nw.y2);}
void sol(int l,int r,int ql,int qr){
if(ql>qr) return ;
if(l==r){
for(int i=ql;i<=qr;i++) ans[id[i]]=a[l].v;
return;
}
int mid=(l+r)/2;
for(int i=l;i<=mid;i++) t.upd(a[i].x,a[i].y,1);
int tp1=0,tp2=0;
for(int i=ql;i<=qr;i++){
int u=id[i],s=cur[u]+qry(q[u]);
if(s>=q[u].k) t1[++tp1]=u;
else t2[++tp2]=u,cur[u]=s;
}
for(int i=l;i<=mid;i++) t.upd(a[i].x,a[i].y,-1);
int cnt=ql-1;
for(int i=1;i<=tp1;i++) id[++cnt]=t1[i];
for(int i=1;i<=tp2;i++) id[++cnt]=t2[i];
sol(l,mid,ql,ql+tp1-1);
sol(mid+1,r,ql+tp1,qr);
}
int main(){
/*2023.23.26 H_W_Y P1527 [国家集训队] 矩阵乘法 整体二分*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;t.init();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
int nw=(i-1)*n+j;
cin>>a[nw].v;
a[nw].x=i;a[nw].y=j;
}
for(int i=1;i<=m;i++){
cin>>q[i].x1>>q[i].y1>>q[i].x2>>q[i].y2>>q[i].k;
id[i]=i;
}
sort(a+1,a+n*n+1);
sol(1,n*n,1,m);
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P3703 树点涂色 - 树剖 + SGT + 颜色段均摊
Bob 有一棵 \(n\) 个点的有根树,其中 \(1\) 号点是根节点。Bob 在每个点上涂了颜色,并且每个点上的颜色不同。
定义一条路径的权值是:这条路径上的点(包括起点和终点)共有多少种不同的颜色。
Bob可能会进行这几种操作:
1 x表示把点 \(x\) 到根节点的路径上所有的点染上一种没有用过的新颜色。
2 x y求 \(x\) 到 \(y\) 的路径的权值。
3 x在以 \(x\) 为根的子树中选择一个点,使得这个点到根节点的路径权值最大,求最大权值。Bob一共会进行 \(m\) 次操作
\(1\leq n \leq 10^5\),\(1\leq m \leq 10^5\)。
首先对于这种染色问题——一眼颜色段均摊,
于是每一次修改就直接是修改一段相同的区间的颜色。
我们还是考虑用树剖来维护,容易想到可以用线段树维护每一个位置到根节点的权值,设为 \(val[u]\),
于是对于 \(3\) 操作,就是一个区间查询,
而 \(2\) 操作,就直接是一个 \(val[u]+val[v]-2 \times val[lca]+1\),这很容易想到。
那么我们的问题就变成了 \(1\) 操作的维护。
还是类似于颜色段均摊的做法对于每一种颜色分别修改,
那么我们维护每一种颜色的 \(st\) 和 \(ed\),把 \(x\) 到 \(1\) 的修改变成一段一段的颜色修改,
而过程中每次我们需要对那一个子树内的点的 \(val\) 进行修改,
这就是一个区间的加法,每次减去 \(val[u]-1\)。
而画图中我们会发现下面的点会被操作多次,于是只需要记录一个 \(lst\),每次改一次改回去就可以了。
这样就做完了,具体还是要看代码。(没什么细节)
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=2e5+5;
int n,m,son[N],sz[N],top[N],fa[N],dep[N],f[N][20],dfn[N],idx=0,rev[N],col,to[N],frm[N],ed[N];
vector<int> g[N];
void dfs1(int u,int pre){
son[u]=-1;sz[u]=1;fa[u]=f[u][0]=pre;dep[u]=dep[pre]+1;
for(int i=1;i<=16;i++) f[u][i]=f[f[u][i-1]][i-1];
for(auto v:g[u]){
if(v==pre) continue;
dfs1(v,u);
sz[u]+=sz[v];
if(son[u]==-1||sz[son[u]]<sz[v]) son[u]=v;
}
}
void dfs2(int u,int pre){
top[u]=pre;dfn[u]=++idx;rev[idx]=u;
if(son[u]==-1){ed[u]=idx;return;}
dfs2(son[u],pre);
for(auto v:g[u]) if(v!=fa[u]&&v!=son[u]) dfs2(v,v);
ed[u]=idx;
}
int climb(int u,int v){
for(int i=16;i>=0;i--) if(dep[f[u][i]]>dep[v]) u=f[u][i];
return u;
}
namespace SGT{
struct sgt{int mx,col,tag;}tr[N<<2];
#define mid ((l+r)>>1)
#define lc p<<1
#define rc p<<1|1
#define lson l,mid,lc
#define rson mid+1,r,rc
void pu(int p){tr[p].mx=max(tr[lc].mx,tr[rc].mx);}
void pd(int p){
if(tr[p].tag){
tr[lc].tag+=tr[p].tag;tr[rc].tag+=tr[p].tag;
tr[lc].mx+=tr[p].tag,tr[rc].mx+=tr[p].tag;
tr[p].tag=0;
}
if(tr[p].col){
tr[lc].col=tr[rc].col=tr[p].col;
tr[p].col=0;
}
}
void build(int l,int r,int p){
if(l==r){
tr[p].mx=dep[rev[l]],tr[p].col=rev[l];
return;
}
build(lson);build(rson);pu(p);
}
void upd(int l,int r,int p,int x,int y,int v){
if(x<=l&&y>=r) return tr[p].tag+=v,tr[p].mx+=v,void();
pd(p);
if(x<=mid) upd(lson,x,y,v);
if(y>mid) upd(rson,x,y,v);
pu(p);
}
void updcol(int l,int r,int p,int x,int y,int v){
if(x<=l&&y>=r) return tr[p].col=v,void();
pd(p);
if(x<=mid) updcol(lson,x,y,v);
if(y>mid) updcol(rson,x,y,v);
pu(p);
}
int qry(int l,int r,int p,int x,int y){
if(x<=l&&y>=r) return tr[p].mx;
pd(p);
if(y<=mid) return qry(lson,x,y);
if(x>mid) return qry(rson,x,y);
return max(qry(lson,x,y),qry(rson,x,y));
}
int qrycol(int l,int r,int p,int x){
if(l==r) return tr[p].col;
pd(p);
return (x<=mid)?qrycol(lson,x):qrycol(rson,x);
}
}
using namespace SGT;
void mof(int u,int v,int lst){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
int nw=qry(1,n,1,dfn[u],dfn[u]);
upd(1,n,1,dfn[top[u]],ed[top[u]],1-nw);
if(lst) upd(1,n,1,dfn[lst],ed[lst],nw-1);
updcol(1,n,1,dfn[top[u]],dfn[u],col);
lst=top[u],u=fa[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
int nw=qry(1,n,1,dfn[u],dfn[u]);
upd(1,n,1,dfn[u],ed[u],1-nw);
if(lst) upd(1,n,1,dfn[lst],ed[lst],nw-1);
updcol(1,n,1,dfn[u],dfn[v],col);
}
void change(int u){
frm[++col]=u;to[col]=1;
int lst=0;
while(u){
int nw=qrycol(1,n,1,dfn[u]),TO=to[nw];
if(frm[nw]==u) frm[nw]=to[nw]=0;
else to[nw]=climb(frm[nw],u),upd(1,n,1,dfn[to[nw]],ed[to[nw]],1);
mof(u,TO,lst);
lst=TO,u=fa[TO];
}
}
int LCA(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
u=fa[top[u]];
}
return dep[u]<dep[v]?u:v;
}
int main(){
/*2023.12.28 H_W_Y P3703 [SDOI2017] 树点涂色 树剖*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;col=n;
for(int i=1,u,v;i<n;i++) cin>>u>>v,g[u].pb(v),g[v].pb(u);
for(int i=1;i<=n;i++) frm[i]=to[i]=i;
dfs1(1,0);dfs2(1,1);build(1,n,1);
for(int i=1,op,u,v;i<=m;i++){
cin>>op>>u;
if(op==1) change(u);
else if(op==2){
cin>>v;int lca=LCA(u,v);
cout<<(qry(1,n,1,dfn[u],dfn[u])+qry(1,n,1,dfn[v],dfn[v])-2*qry(1,n,1,dfn[lca],dfn[lca])+1)<<'\n';
}else cout<<qry(1,n,1,dfn[u],ed[u])<<'\n';
}
return 0;
}
P3722 影魔 - 区间子区间 + BIT
奈文摩尔有 \(n\) 个灵魂,他们在影魔宽广的体内可以排成一排,从左至右标号 \(1\) 到 \(n\)。第 \(i\) 个灵魂的战斗力为 \(k_i\),灵魂们以点对的形式为影魔提供攻击力。对于灵魂对 \(i, j\ (i<j)\) 来说,若不存在 \(k_s\ (i<s<j)\) 大于 \(k_i\) 或者 \(k_j\),则会为影魔提供 \(p_1\) 的攻击力。另一种情况,令 \(c\) 为 \(k_{i + 1}, k_{i + 2}, \cdots, k_{j -1}\) 的最大值,若 \(c\) 满足:\(k_i < c < k_j\),或者 \(k_j < c < k_i\),则会为影魔提供 \(p_2\) 的攻击力,当这样的 \(c\) 不存在时,自然不会提供这 \(p_2\) 的攻击力;其他情况的点对,均不会为影魔提供攻击力。
影魔的挚友噬魂鬼在一天造访影魔体内时被这些灵魂吸引住了,他想知道,对于任意一段区间 \([a, b]\),位于这些区间中的灵魂对会为影魔提供多少攻击力,即考虑所有满足 \(a\le i<j\le b\) 的灵魂对 \(i, j\) 提供的攻击力之和。
顺带一提,灵魂的战斗力组成一个 \(1\) 到 \(n\) 的排列:\(k_1, k_1, \cdots, k_n\)。
\(1\le n,m\le 200000, 1\le p_1, p_2\le 1000\)。
看到区间子区间就容易想到 lxl 的扫描线。
但是这道题的扫描线又没有普通的那么复杂,只需要差分就可以了。
首先还是对每一个树的贡献进行讨论,
对于第 \(i\) 个位置的点,我们让它就是题目中的 \(c\),那么这样它的贡献就是很好算的了。
可以用单调栈先预处理出左右两边第一个比 \(i\) 大的点 \(L[i]\) 和 \(R[i]\),
于是对于区间 \([L[i],R[i]]\) 它对答案的贡献是 \(p_1\),
而对于区间 \([L[i]+1 \sim i-1,R[i]]\) 和 \([L[i],i+1\sim R[i]-1]\),它对答案的贡献是 \(p_2\),
我们就可以把这些写出来,再用一个树状数组维护差分即可。
这样对于询问就直接在 \(l-1\) 和 \(r\) 时分别查 \([l,r]\) 的贡献即可。
树状数组维护的差分前缀和还是比较妙的,我们单独用一个数组维护要减去的值即可,具体见代码。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+5;
int n,m,p1,p2,a[N],cnt=0,L[N],R[N],it1,it2,st[N],tp=0;
ll ans[N];
struct node{
int x,l,r,v,id;
bool operator <(const node &rhs) const{
return x<rhs.x;
}
}q[N<<1],op[N<<1];
namespace BIT{
ll c1[N],c2[N];
int lowbit(int i){return i&(-i);}
void upd(int x,int v){
if(x) for(int i=x;i<=n;i+=lowbit(i)) c1[i]+=v,c2[i]+=1ll*v*(x-1);
}
ll qry(int x){
ll res=0;
for(int i=x;i>=1;i-=lowbit(i)) res+=1ll*c1[i]*x-c2[i];
return res;
}
}
using namespace BIT;
int main(){
/*2023.12.27 H_W_Y P3722 [AH2017/HNOI2017] 影魔 BIT*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>p1>>p2;
for(int i=1;i<=n;i++) cin>>a[i];
a[0]=a[n+1]=n+1;st[++tp]=0;
for(int i=1;i<=n+1;i++){
while(tp&&a[i]>a[st[tp]]) R[st[tp]]=i,--tp;
L[i]=st[tp];st[++tp]=i;
}
for(int i=1,l,r;i<=m;i++){
cin>>l>>r;ans[i]=1ll*(r-l)*p1;
q[2*i-1]=(node){l-1,l,r,-1,i};
q[2*i]=(node){r,l,r,1,i};
}
for(int i=1;i<=n;i++){
if(L[i]&&R[i]<=n) op[++cnt]=(node){R[i],L[i],L[i],p1,0};
if(L[i]+1<i&&R[i]<=n) op[++cnt]=(node){R[i],L[i]+1,i-1,p2,0};
if(L[i]&&R[i]>i+1) op[++cnt]=(node){L[i],i+1,R[i]-1,p2,0};
}
sort(q+1,q+2*m+1);sort(op+1,op+cnt+1);
it1=it2=1;
while(!q[it2].x) ++it2;
for(int i=1;i<=n&&it2<=2*m;i++){
while(it1<=cnt&&op[it1].x==i) upd(op[it1].l,op[it1].v),upd(op[it1].r+1,-op[it1].v),++it1;
while(it2<=m*2&&q[it2].x==i) ans[q[it2].id]+=1ll*q[it2].v*(qry(q[it2].r)-qry(q[it2].l-1)),++it2;
}
for(int i=1;i<=m;i++) cout<<ans[i]<<'\n';
return 0;
}
P5280 [ZJOI2019] 线段树 - 分类讨论
九条可怜是一个喜欢数据结构的女孩子,在常见的数据结构中,可怜最喜欢的就是线段树。
线段树的核心是懒标记,下面是一个带懒标记的线段树的伪代码,其中 \(tag\) 数组为懒标记:
其中函数 \(\operatorname{Lson}(Node)\) 表示 \(Node\) 的左儿子,\(\operatorname{Rson}(Node)\) 表示 \(Node\) 的右儿子。
现在可怜手上有一棵 \([1,n]\) 上的线段树,编号为 \(1\)。这棵线段树上的所有节点的 \(tag\) 均为\(0\)。接下来可怜进行了 \(m\) 次操作,操作有两种:
\(1\ l\ r\),假设可怜当前手上有 \(t\) 棵线段树,可怜会把每棵线段树复制两份(\(tag\) 数组也一起复制),原先编号为 \(i\) 的线段树复制得到的两棵编号为 \(2i-1\) 与 \(2i\),在复制结束后,可怜手上一共有 \(2t\) 棵线段树。接着,可怜会对所有编号为奇数的线段树进行一次 \(\operatorname{Modify}(root,1,n,l,r)\)。
\(2\),可怜定义一棵线段树的权值为它上面有多少个节点 \(tag\) 为 \(1\)。可怜想要知道她手上所有线段树的权值和是多少。
\(1 \le n,m \le 10^5\)。
感觉可以分成每一个节点被操作的次数讨论,理论上可能也是可以的。
但是有点过于复杂了,我们考虑 \(n\) 次 \(1\) 操作之后一共有 \(2^n\) 棵线段树,
那么我们其实可以考虑每一个节点为 \(1\) 的概率。
我们设 \(f[u]\) 表示 \(u\) 节点被打标记的概率,\(g[u]\) 表示 \(u\) 到根的路径上有标记的概率。
那么每一次的区间操作我们就有了一些变化。
- 经过而不打标记的点,那么它的标记一定被下传了,而有一半线段树不会变,于是变为 \(\{\frac{1}{2}f[u],\frac{1}{2}g[u]\}\)。
- 经过而要打标记的点,那么它一定是包含在区间内部的,\(\{ \frac{1}{2}f[u]+\frac{1}{2},\frac{1}{2} g[u] + \frac{1}{2} \}\)。
- 父亲被经过了,而自己和区间无关,于是标记一定会下传下来,\(\{ \frac{1}{2}(f[u]+g[u]),g[u] \}\)。
- 被包含在修改区间内,自己又不打标记,\(\{ f[u],\frac{1}{2} g[u] + \frac{1}{2} \}\)。
- 包含在第 \(3\) 类点里面,不变。
容易发现对于前 \(3\) 种我们可以直接暴力操作,因为一共就只有 \(\log\) 个,
而对于第 \(4\) 种,我们需要打标记,而发现这个标记也是好维护的,具体见代码。
于是这样直接用线段树模拟一下就可以了,最后就是维护一个 \(f[u]\) 的和即可。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+5,mod=998244353,inv2=499122177;
int n,m,cnt=1,f[N<<2],g[N<<2],t[N<<2],s[N<<2];
#define mid ((l+r)>>1)
#define lson l,mid,p<<1
#define rson mid+1,r,p<<1|1
#define lc p<<1
#define rc p<<1|1
int add(int x,int y){return (x+=y)>=mod?x-mod:x;}
void pu(int p,bool vis){
if(vis) s[p]=f[p];
else s[p]=add(f[p],add(s[lc],s[rc]));
}
void tag(int p,int x){
g[p]=(1ll*g[p]*x%mod+1-x+mod)%mod;
t[p]=1ll*t[p]*x%mod;
}
void pd(int p){
tag(lc,t[p]);tag(rc,t[p]);t[p]=1;
}
void build(int l,int r,int p){
t[p]=1;
if(l==r) return ;
build(lson),build(rson);
}
void upd(int l,int r,int p,int x,int y){
if(y<l||x>r){
f[p]=1ll*(f[p]+g[p])*inv2%mod;
pu(p,(l==r));return;
}
if(x<=l&&y>=r){
f[p]=1ll*(f[p]+1)*inv2%mod;
pu(p,(l==r));tag(p,inv2);
return;
}
pd(p);
f[p]=1ll*inv2*f[p]%mod;
g[p]=1ll*inv2*g[p]%mod;
upd(lson,x,y);upd(rson,x,y);pu(p,0);
}
int main(){
/*2023.12.26 H_W_Y P5280 [ZJOI2019] 线段树 SGT*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;cnt=1;build(1,n,1);
for(int i=1,op,l,r;i<=m;i++){
cin>>op;
if(op==1) cin>>l>>r,upd(1,n,1,l,r),cnt=add(cnt,cnt);
else cout<<(1ll*cnt*s[1]%mod)<<'\n';
}
return 0;
}
CF768G The Winds of Winter - DSU on Tree
给一个有根树。若我们删去一个节点和所有与他相连的边,则会得到一个森林。你希望这个森林中节点最多的树的节点个数尽量少,于是你可以进行至多一次如下操作:删除一个节点和其父亲之间的边,把这个节点连到某个节点上。这个操作不得改变森林中树的个数。
对于每个节点,输出它作为删去的节点时,进行至多一次操作后的最大树大小的最小值。
\(1 \le n \le 10^5\)。
看起来就很像 DSU on Tree,
因为贪心算一下我们一定是把最大的子树中扒出来一些拼到最小的树上面,
而答案是可以二分得到的,每次的判断我们需要用到 set 去维护子树外的点和子树内的点。
首先重儿子可以预处理出来,那么问题就成了如何解决子树外的点的维护,
看代码似乎更容易理解,直接用 lxs 表示
我们考虑最开始就全部加进来,而每次操作之后保证这个集合里面不存在这棵子树中的点即可,
于是处理之后进行二分,最后启发式合并一下即可,
时间复杂度是 \(\mathcal O(n \log^2n)\) 的。
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define lb lower_bound
const int N=1e5+5;
int n,rt,fa[N],son[N],mx[N],mn[N],smx[N],sz[N],ans[N];
vector<int> g[N];
multiset<int> pre,lxs,s[N];
void dfs(int u,int FA){
sz[u]=1;fa[u]=FA;
for(auto v:g[u]){
if(v==fa[u]) continue;
dfs(v,u);sz[u]+=sz[v];
if(!son[u]||sz[son[u]]<sz[v]) son[u]=v;
}
if(u!=rt) lxs.insert(sz[u]);
}
bool chk(int v,int u){
if(mx[u]==sz[son[u]]){
auto it=s[u].lb(mx[u]-v);
return (it!=s[u].end()&&*it<=v-mn[u]);
}else{
auto it=lxs.lb(mx[u]-v);
if(it!=lxs.end()&&*it<=v-mn[u]) return true;
it=pre.lb(mx[u]-v+sz[u]);
return (it!=pre.end()&&*it<=v-mn[u]+sz[u]);
}
}
void sol(int u){
if(u!=rt){
lxs.erase(lxs.find(sz[u]));
if(fa[u]!=rt) pre.insert(sz[fa[u]]);
}
mx[u]=max(n-sz[u],sz[son[u]]);
smx[u]=min(n-sz[u],sz[son[u]]);
mn[u]=n-sz[u];
for(auto v:g[u]){
if(v==fa[u]||v==son[u]) continue;
sol(v);
for(auto t:s[v]) lxs.insert(t);
}
if(son[u]){
sol(son[u]);swap(s[u],s[son[u]]);
mn[u]=min(mn[u],sz[son[u]]);
if(!mn[u]) mn[u]=sz[son[u]];
}
for(auto v:g[u]){
if(v==fa[u]||v==son[u]) continue;
mn[u]=min(mn[u],sz[v]);
smx[u]=max(smx[u],sz[v]);
for(auto t:s[v]) lxs.erase(lxs.find(t));
}
if(mx[u]!=smx[u]){
int l=smx[u],r=mx[u];
while(l<=r){
int mid=(l+r)/2;
if(chk(mid,u)) ans[u]=mid,r=mid-1;
else l=mid+1;
}
}
if(!ans[u]) ans[u]=mx[u];
for(auto v:g[u]){
if(v==fa[u]||v==son[u]) continue;
for(auto t:s[v]) s[u].insert(t);
}
if(u!=rt&&fa[u]!=rt) pre.erase(pre.find(sz[fa[u]]));
s[u].insert(sz[u]);
}
int main(){
/*2023.12.26 H_W_Y CF768G The Winds of Winter DSU on Tree*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1,u,v;i<=n;i++){
cin>>u>>v;
if(!u||!v) rt=u+v;
else g[u].pb(v),g[v].pb(u);
}
dfs(rt,0);sol(rt);
for(int i=1;i<=n;i++) cout<<ans[i]<<'\n';
return 0;
}
P5210 [ZJOI2017] 线段树 - zkw
最近可怜又开始研究起线段树来了,有所不同的是,她把目光放在了更广义的线段树上:在正常的线段树中,对于区间 \([l, r]\),我们会取 \(m = \lfloor \frac{l+r}{2} \rfloor\),然后将这个区间分成 \([l, m]\) 和 \([m + 1, r]\) 两个子区间。在广义的线段树中,\(m\) 不要求恰好等于区间的中点,但是 \(m\) 还是必须满足 \(l \le m < r\) 的。不难发现在广义的线段树中,树的深度可以达到 \(O(n)\) 级别。
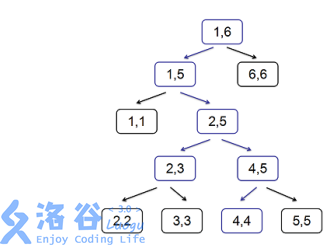
例如下面这棵树,就是一棵广义的线段树:
为了方便,我们按照先序遍历给线段树上所有的节点标号,例如在上图中,\([2, 3]\) 的标号是 \(5\),\([4, 4]\) 的标号是 \(9\),不难发现在 \([1, n]\) 上建立的广义线段树,它共有着 \(2n − 1\) 个节点。
考虑把线段树上的定位区间操作 \((\)就是打懒标记的时候干的事情\()\) 移植到广义线段树上,可以发现在广义的线段树上还是可以用传统的线段树上的方法定位区间的,例如在上图中,蓝色节点和蓝色边就是在定位区间 \([2, 4]\) 时经过的点和边,最终定位到的点是 \([2, 3]\) 和 \([4, 4]\)。
如果你对线段树不熟悉,这儿给出定位区间操作形式化的定义:给出区间 \([l, r]\),找出尽可能少的区间互不相交的线段树节点,使得它们区间的并集恰好是 \([l, r]\)。
定义 \(S_{[l,r]}\) 为定位区间 \([l, r]\) 得到的点集,例如在上图中,\(S_{[2,4]} = \{5, 9\}\)。定义线段树上两个点 \(u, v\) 的距离 \(d(u, v)\) 为线段树上 \(u\) 到 \(v\) 最短路径上的边数,例如在上图中 \(d(5, 9) = 3\)。
现在可怜给了你一棵 \([1, n]\) 上的广义的线段树并给了 \(m\) 组询问,每组询问给出三个数 \(u, l, r\ (l \le r)\),可怜想要知道 \(\sum_{v \in S_{[l, r]}} d(u, v)\)。
\(1 \le n,m \le 2 \times 10^5\)。
又是一个线段树。
感觉就挺奇怪的,我们考虑用类似于 ZKW 线段树的处理区间询问的方法来处理。
也就是我们对于区间 \([l,r]\) 的标记操作,我们考虑这些区间的位置其实是 \(l-1,r+1\) 的位置到他们的 LCA 除中间夹道的节点,
也就是 \(pos[l-1] \to lca\) 路径上每一个节点的右儿子,\(pos[r+1] \to lca\) 路径上每一个节点的左儿子。
而最终求的就是有关 lca 的深度的东西,所以我们可以直接先预处理出这个东西,
直接差分就可以求到 dep 之和。
那么现在问题就转化成了 \(-2 \times dep[lca]\),而 \(lca\) 的具体位置我们有需要分类讨论,
设 \(l-1,r+1\) 的 LCA 为 \(x\),
那么一共有三种情况,\(u\) 在 \(x\) 的上面,于是 LCA 一定是 \(u\),直接减去即可。
而还有两种就是 \(u\) 在 \(x\) 的左右子树的情况,直接讨论一下,贡献还是很好算的。
这样我们就做完了。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5e5+5;
int n,m,pos[N],cnt=0,ch[N][2],c[N][2],f[N][20],dep[N],dfn[N],sz[N],rt,idx=0;
ll s[N][2],ans=0;
int build(int l,int r){
int p=++cnt,mid;
if(l==r) return pos[l]=p,p;
cin>>mid;
ch[p][0]=build(l,mid);
ch[p][1]=build(mid+1,r);
return p;
}
void dfs1(int u,int fa){
if(!u) return;
f[u][0]=fa;dep[u]=dep[fa]+1;dfn[u]=++idx;
for(int i=1;f[f[u][i-1]][i-1];i++) f[u][i]=f[f[u][i-1]][i-1];
dfs1(ch[u][0],u);dfs1(ch[u][1],u);
sz[u]=sz[ch[u][0]]+sz[ch[u][1]]+1;
}
void dfs2(int u){
for(int i=0;i<2;i++)
if(ch[u][i]){
for(int j=0;j<2;j++) c[ch[u][i]][j]=c[u][j],s[ch[u][i]][j]=s[u][j];
if(ch[u][i^1]) ++c[ch[u][i]][i^1],s[ch[u][i]][i^1]+=dep[ch[u][i^1]];
dfs2(ch[u][i]);
}
}
int LCA(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=18;i>=0;i--)
if(dep[f[u][i]]>=dep[v]) u=f[u][i];
if(u==v) return u;
for(int i=18;i>=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
return f[u][0];
}
int main(){
/*2023.12.26 H_W_Y P5210 [ZJOI2017] 线段树 zkw 的思路*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;build(1,n);
rt=++cnt;
ch[rt][0]=pos[0]=++cnt;ch[rt][1]=1;
rt=++cnt;
ch[rt][1]=pos[n+1]=++cnt;ch[rt][0]=rt-2;
dfs1(rt,0);dfs2(rt);
cin>>m;
for(int u,l,r,lc,rc,lca,x;m;m--){
cin>>u>>l>>r;
lca=LCA(l=pos[l-1],r=pos[r+1]);lc=ch[lca][0],rc=ch[lca][1];
ans=s[l][1]-s[lc][1]+s[r][0]-s[rc][0]+1ll*dep[u]*(c[l][1]-c[lc][1]+c[r][0]-c[rc][0]);
if(dfn[lca]>=dfn[u]||dfn[u]>=dfn[lca]+sz[lca]){
x=LCA(lca,u);
ans-=2ll*dep[x]*(c[l][1]-c[lc][1]+c[r][0]-c[rc][0]);
}else if(dfn[u]>=dfn[lc]&&dfn[u]<dfn[lc]+sz[lc]){
x=LCA(l,u);
ans-=2ll*dep[lca]*(c[r][0]-c[rc][0]);
ans-=2ll*(s[x][1]-s[lc][1]-c[x][1]+c[lc][1]);
ans-=2ll*dep[x]*(c[l][1]-c[x][1]);
if(dfn[u]>=dfn[ch[x][1]]&&dfn[u]<dfn[ch[x][1]]+sz[ch[x][1]]) ans-=2;
}else{
x=LCA(r,u);
ans-=2ll*dep[lca]*(c[l][1]-c[lc][1]);
ans-=2ll*(s[x][0]-s[rc][0]-c[x][0]+c[rc][0]);
ans-=2ll*dep[x]*(c[r][0]-c[x][0]);
if(dfn[u]>=dfn[ch[x][0]]&&dfn[u]<dfn[ch[x][0]]+sz[ch[x][0]]) ans-=2;
}
cout<<ans<<'\n';
}
return 0;
}
P5324 删数 - SGT - 好题!
对于任意一个数列,如果能在有限次进行下列删数操作后将其删为空数列,则称这个数列可以删空。一次删数操作定义如下:
记当前数列长度为 \(k\) ,则删掉数列中所有等于 \(k\) 的数。
现有一个长度为 \(n\) 的数列 \(a\),有 \(m\) 次修改操作,第 \(i\) 次修改后你要回答:
经过 \(i\) 次修改后的数列 \(a\),至少还需要修改几个数才可删空?
每次修改操作为单点修改或数列整体加一或数列整体减一。
\(1\le n,m \le 150000,1\le a_i \le n,0\le p\le n\),\(p>0\)时,\(1\le x \le n\)。
首先我们需要发现一个性质——感觉可以直接手玩一下就可以得到,
假设 \(i\) 的出现次数为 \(cnt_i\),我们将 \([i-cnt_i+1,i]\) 中的数都 \(+1\),
那么答案就是 \([1,n]\) 中 \(0\) 的那些位置的个数。
于是我们就做完了,直接用线段树维护最小值和最小值出现次数即可,
注意每一次整体加减的时候要把边缘的贡献减掉,不然会算重!
#include <bits/stdc++.h>
using namespace std;
const int N=6e5+5;
int n,m,L,R,delta,c[N],a[N];
namespace SGT{
struct sgt{int mn,c,t;}tr[N<<2];
#define mid ((l+r)>>1)
#define lc p<<1
#define rc p<<1|1
#define lson l,mid,lc
#define rson mid+1,r,rc
sgt merge(sgt x,sgt y){
sgt res=(sgt){0,0,0};
res.mn=min(x.mn,y.mn);
if(x.mn==res.mn) res.c+=x.c;
if(y.mn==res.mn) res.c+=y.c;
return res;
}
void pu(int p){tr[p]=merge(tr[lc],tr[rc]);}
void pd(int p){
if(!tr[p].t) return;
tr[lc].mn+=tr[p].t,tr[rc].mn+=tr[p].t;
tr[lc].t+=tr[p].t,tr[rc].t+=tr[p].t;
tr[p].t=0;
}
void upd(int l,int r,int p,int x,int v){
if(l==r) return tr[p].mn+=v,void();pd(p);
(x<=mid)?upd(lson,x,v):upd(rson,x,v);pu(p);
}
void mof(int l,int r,int p,int x,int y,int v){
if(x>y) return ;
if(x<=l&&y>=r) return tr[p].mn+=v,tr[p].t+=v,void();pd(p);
if(x<=mid) mof(lson,x,y,v);
if(y>mid) mof(rson,x,y,v);pu(p);
}
void build(int l,int r,int p){
if(l==r) return tr[p].mn=0,tr[p].c=1,void();
build(lson);build(rson);pu(p);
}
sgt qry(int l,int r,int p,int x,int y){
if(x<=l&&y>=r) return tr[p];pd(p);
if(y<=mid) return qry(lson,x,y);
if(x>mid) return qry(rson,x,y);
return merge(qry(lson,x,y),qry(rson,x,y));
}
}
using namespace SGT;
int main(){
/*2023.12.27 H_W_Y P5324 [BJOI2019] 删数 SGT*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;L=-m-n,R=n+m;delta=0;build(L,R,1);
for(int i=1;i<=n;i++) cin>>a[i],++c[a[i]+m];
for(int i=1;i<=n;i++) mof(L,R,1,i-c[i+m]+1,i,1);
for(int i=1,p,x;i<=m;i++){
cin>>p>>x;
if(p==0){
if(x==1) mof(L,R,1,n-delta-c[n-delta+m]+1,n-delta,-1),delta+=x;
else delta+=x,mof(L,R,1,n-delta-c[n-delta+m]+1,n-delta,1);
}
else{
x-=delta;
if(a[p]<=n-delta) upd(L,R,1,a[p]-c[a[p]+m]+1,-1);--c[a[p]+m];
upd(L,R,1,x-c[x+m],1);++c[x+m];a[p]=x;
}
sgt ans=qry(L,R,1,1-delta,n-delta);
if(ans.mn==0) cout<<ans.c<<'\n';
else cout<<"0\n";
}
return 0;
}
P6773 [NOI2020] 命运 - dp + 线段树合并
形式化的:给定一棵树 \(T = (V, E)\) 和点对集合 \(\mathcal Q \subseteq V \times V\) ,满足对于所有 \((u, v) \in \mathcal Q\),都有 \(u \neq v\),并且 \(u\) 是 \(v\) 在树 \(T\) 上的祖先。其中 \(V\) 和 \(E\) 分别代表树 \(T\) 的结点集和边集。求有多少个不同的函数 \(f\) : \(E \to \{0, 1\}\)(将每条边 \(e \in E\) 的 \(f(e)\) 值置为 \(0\) 或 \(1\)),满足对于任何 \((u, v) \in \mathcal Q\),都存在 \(u\) 到 \(v\) 路径上的一条边 \(e\) 使得 \(f(e) = 1\)。由于答案可能非常大,你只需要输出结果对 \(998,244,353\)(一个素数)取模的结果。
\(n \leq 5 \times 10^5\),\(m \leq 5 \times 10^5\)。输入构成一棵树,并且对于 \(1 \leq i \leq m\),\(u_i\) 始终为 \(v_i\) 的祖先结点。
没保存,寄。
首先感觉就是一眼的 dp,就是记 \(f[u][i]\) 表示处理完 \(u\) 的子树中,剩下没有被选中的边的上端点最深深度为 \(i\),的方案数。
自己列出来了,但是方程不会写了,于是写错了,——原来我们的实力更多的是 dp 的问题。
我们只需要记录深度最深的,因为其他的没意义嘛。
于是可以列出 dp 方程式:
前面的一个是要选的,后面则是不选。
这样我们用前缀和优化一下就变成了这个样子,设 \(g_{u,i}= \sum_{j=0}^i f_{u,i}\),
于是你就可以得到了 \(\mathcal O(n^2)\) 的做法了。
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=5e5+5,mod=998244353,M=1e3+5;
int n,m,dep[N],f[M<<1][M],g[M<<1][M],ans=0;
vector<int> G[N],p[N];
void ad(int &x,int y){x+=y;if(x>mod) x-=mod;}
int mul(int x,int y){return 1ll*x*y%mod;}
void merge(int u,int v){
for(int i=0;i<dep[u];i++) f[u][i]=(1ll*f[u][i]*(g[v][dep[u]]+g[v][i])%mod+1ll*g[u][i-1]*f[v][i]%mod)%mod;
for(int i=0;i<dep[u];i++) g[u][i]=((i?g[u][i-1]:0)+f[u][i])%mod;
}
void dp(int u,int fa){
int mx=0;dep[u]=dep[fa]+1;
for(auto v:p[u]) mx=max(mx,dep[v]);
f[u][mx]=1;
for(int i=0;i<=dep[u];i++) g[u][i]=((i?g[u][i-1]:0)+f[u][i])%mod;
for(auto v:G[u]) if(v!=fa) dp(v,u),merge(u,v);
}
int main(){
/*2023.12.30 H_W_Y P6773 [NOI2020] 命运 dp*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;i++) cin>>u>>v,G[u].pb(v),G[v].pb(u);
cin>>m;
for(int i=1,u,v;i<=m;i++) cin>>u>>v,p[v].pb(u);
dp(1,0);
cout<<f[1][0]<<'\n';
return 0;
}
接下来我们就用上高贵的线段树合并,
做到一边计算前缀和一边合并,这样就可以做到 \(\mathcal O(n \log n)\) 了。
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=5e5+5,mod=998244353,M=1e3+5;
int n,m,dep[N],ans=0;
vector<int> G[N],p[N];
void mul(int &x,int y){x=1ll*x*y%mod;}
void add(int &x,int y){x+=y;if(x>=mod) x-=mod;}
namespace SGT{
int rt[N],idx=0;
struct sgt{int s[2],v,t;}tr[N<<5];
#define mid ((l+r)>>1)
#define lc(p) tr[p].s[0]
#define rc(p) tr[p].s[1]
void pu(int p){tr[p].v=(tr[lc(p)].v+tr[rc(p)].v)%mod;}
void pd(int p){
if(tr[p].t==1) return;
mul(tr[lc(p)].t,tr[p].t);
mul(tr[rc(p)].t,tr[p].t);
mul(tr[lc(p)].v,tr[p].t);
mul(tr[rc(p)].v,tr[p].t);
tr[p].t=1;
}
void upd(int &p,int l,int r,int x,int v){
if(!p) p=++idx,tr[p].t=1;
if(l==r) return tr[p].v=v%mod,void();
pd(p);
(x<=mid)?upd(lc(p),l,mid,x,v):upd(rc(p),mid+1,r,x,v);
pu(p);
}
int qry(int p,int l,int r,int x,int y){
if(x<=l&&y>=r) return tr[p].v;pd(p);
if(y<=mid) return qry(lc(p),l,mid,x,y);
if(x>mid) return qry(rc(p),mid+1,r,x,y);
return (qry(lc(p),l,mid,x,y)+qry(rc(p),mid+1,r,x,y))%mod;
}
int merge(int p1,int p2,int l,int r,int &sv,int &su){
if(!p1&&!p2) return 0;
if(!p1)
return add(sv,tr[p2].v),mul(tr[p2].t,su),mul(tr[p2].v,su),p2;
if(!p2)
return add(su,tr[p1].v),mul(tr[p1].t,sv),mul(tr[p1].v,sv),p1;
if(l==r){
int cu=tr[p1].v;add(sv,tr[p2].v);
tr[p1].v=(1ll*tr[p1].v*sv%mod+1ll*su*tr[p2].v%mod)%mod;
add(su,cu);return p1;
}
pd(p1),pd(p2);
lc(p1)=merge(lc(p1),lc(p2),l,mid,sv,su);
rc(p1)=merge(rc(p1),rc(p2),mid+1,r,sv,su);
pu(p1);return p1;
}
}
using namespace SGT;
void dp(int u,int fa){
int mx=0;dep[u]=dep[fa]+1;
for(auto v:p[u]) mx=max(mx,dep[v]);
upd(rt[u],0,n,mx,1);
for(auto v:G[u]) if(v!=fa){
dp(v,u);int su=0,sv=qry(rt[v],0,n,0,dep[u]);
rt[u]=merge(rt[u],rt[v],0,n,sv,su);
}
}
int main(){
/*2023.12.30 H_W_Y P6773 [NOI2020] 命运 dp + 线段树合并*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
for(int i=1,u,v;i<n;i++) cin>>u>>v,G[u].pb(v),G[v].pb(u);
cin>>m;
for(int i=1,u,v;i<=m;i++) cin>>u>>v,p[v].pb(u);
dp(1,0);
cout<<qry(rt[1],0,n,0,0)<<'\n';
return 0;
}
P3733 [HAOI2017] 八纵八横 - 线性基
逐渐离谱。
给一个连通图,每条边有一个 \(len\) 位的二进制数。
支持三种操作: 加一条新边,删一条边,修改一条边。
每次操作后求最大的从 \(1\) 出发回到 \(1\) 的路径异或值。
\(n, m \le 500 ,q, len \le 1000\)。
首先,求最大路径异或值容易想到用 线性基 维护。
而根据 P4151 [WC2011] 最大XOR和路径 我们可以知道,这道题就只需要维护每一条边所在一个环的线性基就可以了。
于是似乎可以直接用线段树分治做了。
但是也并不必要,我们希望维护的就是一个可删除的线性基,
那么贪心地思考,对于最高位,我们希望它的删除时间最晚,
于是在 ins 的过程中加上一个删除时间的维护和比较就可以了。
对于修改边权,我们就把它看作是一次加入一次删除,
离线得到每一条边的删除时间即可。
#include <bits/stdc++.h>
using namespace std;
#define bst bitset<N>
#define pii pair<int,int>
#define fi first
#define se second
const int N=1e3+5,inf=0x3f3f3f3f;
int n,m,q,head[N],tot=0,c1=0,id[N],tim[N],c2=0,op[N],ed[N];
struct edge{int v,nxt;bst w;}e[N<<1];
bool vis[N];
pii g[N];
bst dis[N],d[N],val[N];
string s;
bst read(){cin>>s;bst w(s);return w;}
void prt(bst w){
bool fl=false;
for(int i=999;i>=0;i--){
if(w[i]||fl) putchar(w[i]+'0');
fl|=w[i];
}
if(!fl) putchar('0');putchar('\n');
}
void add(int u,int v){
bst w=read();
e[++tot]=(edge){v,head[u],w};head[u]=tot;
e[++tot]=(edge){u,head[v],w};head[v]=tot;
}
void ins(int t,bst w){
for(int i=1000;i>=0;i--){
if(!w[i]) continue;
if(tim[i]<t) swap(tim[i],t),swap(w,d[i]);
if(!t) return;
w^=d[i];
}
}
void qry(int t){
bst w;
for(int i=1000;i>=0;i--) if(tim[i]>t&&!w[i]) w^=d[i];
prt(w);
}
void dfs(int u){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;bst w=e[i].w;
if(vis[v]) ins(inf,(dis[u]^dis[v]^w));
else dis[v]=dis[u]^w,vis[v]=true,dfs(v);
}
}
int main(){
/*2023.12.27 H_W_Y P3733 [HAOI2017] 八纵八横 线性基*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>q;
for(int i=1,u,v;i<=m;i++) cin>>u>>v,add(u,v);
dfs(1);qry(0);c1=0,c2=q+1;
for(int i=1,x,y;i<=q;i++){
cin>>s;
if(s[1]=='d') cin>>x>>y,op[i]=++c1,val[c1]=(dis[x]^dis[y]^read()),g[c1]={x,y},id[c1]=c1;
if(s[1]=='h') cin>>x,ed[id[x]]=i,op[i]=--c2,val[c2]=(dis[g[x].fi]^dis[g[x].se]^read()),id[x]=c2;
if(s[1]=='a') cin>>x,ed[id[x]]=i;
}
for(int i=1;i<=q;i++) if(!ed[i]) ed[i]=inf;
for(int i=1;i<=q;i++){
if(op[i]) ins(ed[op[i]],val[op[i]]);
qry(i);
}
return 0;
}
P3642 烟火表演 - 可并堆 + 斜率 - 好题!
给定一棵以 \(1\) 为根的 \(n+m\) 个节点的树,每条边有一个边权。有 \(m\) 个叶子。将一条边的边权从 \(x\) 修改至 \(y\) 需要的代价是 \(|x-y|\) 。
求将所有叶子到根节点的距离修改成相同的最小代价。
\(1 \le n+m \le 3 \times 10^5\)。
观察很重要!
感觉就可以用函数表示一下。
首先我们从叶子节点出发,对于一个叶子节点,我们把它连向它的父亲节点时,
只有一条边,那么函数是两段组成,即一段斜率为 \(-1\),一段斜率为 \(1\)。(其实中间还有一段斜率为 \(0\),不过它退化了!)
那么进一步观察,我们设 \(f_u(x)\) 表示在 \(u\) 节点为根的子树中到叶子节点的距离改成 \(x\) 的最小代价,
根据画图可以发现它的图像是一个凸包,从右往左的斜率是 \(sz,sz-1,sz-2,\dots,1,0,-1,\dots\),
而这些斜率可能会退化成点。
为什么呢?(现在不知道可以继续往下看)。
要得到 \(f_u(x)\),我们肯定要从 \(f_v(x)\) 转移过来,而转移过程中就要去考虑 \(u \to v\) 的这条边,假设长度为 \(w\)。
于是我们希望求得一个函数 \(F_v(x)\) 表示 \(v\) 算上到 \(u\) 这条边的函数,
假设 \(f_v(x)\) 中斜率为 \(0\) 的这一段为 \([L,R]\) 那么它一定是最优的,根据贪心的思想,我们可以得到以下结论:
- \(x\lt L\) 时,一定是把 \(w\) 减成 \(0\),因为图像越往左边斜率越小(本来就是负的),\(F(x)=f(x)+w\)。
- \(L \le x \le L+w\),我们还是会把 \(w\) 减小到合适的位置,在用上 \([L,R]\) 这一段的值,\(F(x) = f(L) + w-x+L\)。
- \(L + w\le x \le R+w\),很明显这个 \(w\) 是不用变的,于是 \(F(x) = f(L)\)。
- \(x \gt R+w\),那么我们也是把 \(w\) 增大更优,\(F(x) = f(l)+x-w\)。
这样的贪心推出的式子,我们把它画在图像上面就变成了这个样子:
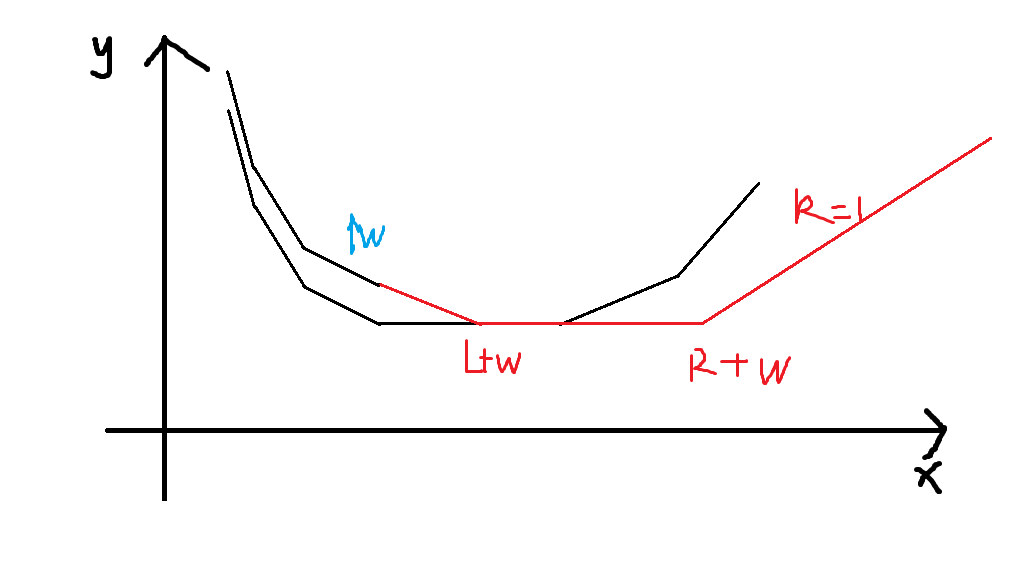
其中黑色是原来的 \(f_v(x)\),本质上一动就是把左边 \(k \lt 0\) 向上平移了 \(w\),而加上两个节点 \(L+w,R+w\) 即可。
那么现在考虑如何合并,
发现这种合并函数就简单了,直接把转折点合并起来就可以了,
得到的函数也是凸的,并且从右往左过程中斜率是从 \(sz,sz-1,\dots\),\(sz\) 表示子树大小,
而这样的斜率我们是可以直接计算它右边的拐点个数得到的,
所以对于每一个拐点,我们只需要维护它的横坐标。
这样一来找 \([L,R]\) 这一段也变得容易了,直接从右往左暴力弹栈即可,
当然这里我们维护的直接是一个可并堆,也就变成暴力弹堆顶,
于是这样就做完了。
最后算答案的时候我们很明显希望找到 \([L,R]\) 区间内纵坐标的值,但这并不好算,
我们可以把它转化成总的(也就是 \(x=0\) 时)来减去减少的,
而我们减少的东西,稍微推一下式子就可以发现其实就是 \(L\) 即之前的横坐标和,
这样最后减去就可以了。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e6+5;
int n,m,fa[N],dep[N],deg[N],lc[N],rc[N],rt[N],idx;
ll ans=0,w[N],val[N];
int nwnode(ll v){val[++idx]=v,dep[idx]=0;return idx;}
int merge(int x,int y){
if(!x||!y) return x+y;
if(val[x]<val[y]) swap(x,y);
rc[x]=merge(rc[x],y);
if(dep[lc[x]]<dep[rc[x]]) swap(lc[x],rc[x]);
dep[x]=dep[rc[x]]+1;
return x;
}
void del(int &x){x=merge(lc[x],rc[x]);}
int main(){
/*2023.12.28 H_W_Y P3642 [APIO2016] 烟火表演 可并堆 + 斜率*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=2;i<=n+m;i++) cin>>fa[i]>>w[i],ans+=w[i],++deg[fa[i]];
for(int u=n+m;u>=2;u--){
if(u<=n) while(deg[u]-->1) del(rt[u]);
ll R=val[rt[u]];del(rt[u]);
ll L=val[rt[u]];del(rt[u]);
rt[u]=merge(rt[u],merge(nwnode(L+w[u]),nwnode(R+w[u])));
rt[fa[u]]=merge(rt[fa[u]],rt[u]);
}
while(deg[1]--) del(rt[1]);
while(rt[1]) ans-=val[rt[1]],del(rt[1]);
cout<<ans<<'\n';
return 0;
}
P4175 网络管理 - 整体二分
给出一个 \(n\) 个节点的树,点有点权,\(q\) 次操作,每次操作分两种:
- 将 \(u\) 点的点权改成 \(v\)。
- 询问 \(u,v\) 路径上面第 \(k\) 大的点权是多少。
\(1 \le n,q \le 8 \times 10^4\)。
感觉就是一道可以用根号做的题,
然后一眼有了 \(4 \log\) 的做法。
而对于这种 \(k\) 大权值的问题,我们还是去考虑整体二分,
于是就做完了,和矩阵乘法(P1527)挺像的,具体可以看代码,就是把 \(1\) 操作拆成了两个。
一发过,好耶~
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=5e5+5;
int n,m,dfn[N],idx=0,ed[N],fa[N],cnt=0,a[N],f[N][20],dep[N],b[N],len,ans[N];
vector<int> g[N];
struct node{int op,l,r,p,v,id;}q[N],t[N];
struct BIT{
int tr[N];
int lowbit(int i){return i&(-i);}
void upd(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=v;}
int qry(int x){
int res=0;x=dfn[x];
for(int i=x;i>=1;i-=lowbit(i)) res+=tr[i];
return res;
}
void mof(int l,int r,int v){
upd(l,v);upd(r+1,-v);
}
}T;
void dfs(int u,int pre){
dfn[u]=++idx;fa[u]=f[u][0]=pre;dep[u]=dep[pre]+1;
for(int i=1;f[f[u][i-1]][i-1];i++) f[u][i]=f[f[u][i-1]][i-1];
for(auto v:g[u]) if(v!=pre) dfs(v,u);
ed[u]=idx;
}
int lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(int i=17;i>=0;i--) if(dep[f[u][i]]>=dep[v]) u=f[u][i];
if(u==v) return u;
for(int i=17;i>=0;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
return f[u][0];
}
void sol(int l,int r,int ql,int qr){
if(ql>qr) return ;
if(l==r){for(int i=ql;i<=qr;i++) if(q[i].op==2) ans[q[i].id]=l;return;}
int mid=((l+r)>>1),c1=ql-1,c2=qr+1;
for(int i=ql;i<=qr;i++){
if(q[i].op==2){
int s=T.qry(q[i].l)+T.qry(q[i].r)-T.qry(q[i].p)-T.qry(fa[q[i].p]);
if(s<q[i].v) q[i].v-=s,t[++c1]=q[i];
else t[--c2]=q[i];
}else if(q[i].v>mid) T.mof(q[i].l,q[i].r,q[i].op),t[--c2]=q[i];
else t[++c1]=q[i];
}
for(int i=ql;i<=qr;i++) if(q[i].op!=2&&q[i].v>mid) T.mof(q[i].l,q[i].r,-q[i].op);
for(int i=ql;i<=qr;i++) q[i]=t[i];reverse(q+c2,q+qr+1);
sol(l,mid,ql,c1);sol(mid+1,r,c2,qr);
}
int main(){
/*2023.12.27 H_W_Y P4175 [CTSC2008] 网络管理 整体二分*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],b[++len]=a[i];
for(int i=1,u,v;i<n;i++) cin>>u>>v,g[u].pb(v),g[v].pb(u);
dfs(1,0);
for(int i=1;i<=n;i++) q[++cnt]=(node){1,dfn[i],ed[i],0,a[i],cnt},ans[cnt]=-1;
for(int i=1,k,u,v;i<=m;i++){
cin>>k>>u>>v;
if(k==0){
b[++len]=v;
q[++cnt]=(node){-1,dfn[u],ed[u],0,a[u],cnt};ans[cnt]=-1;
q[++cnt]=(node){1,dfn[u],ed[u],0,(a[u]=v),cnt};ans[cnt]=-1;
}else q[++cnt]=(node){2,u,v,lca(u,v),k,cnt};
}
b[++len]=-1;sort(b+1,b+len+1);
len=unique(b+1,b+len+1)-b-1;
for(int i=1;i<=cnt;i++){
if(q[i].op!=2) q[i].v=lower_bound(b+1,b+len+1,q[i].v)-b;
}
sol(1,len,1,cnt);
for(int i=1;i<=cnt;i++) if(ans[i]!=-1) (ans[i]>1)?(cout<<b[ans[i]]<<'\n'):(cout<<"invalid request!\n");
return 0;
}
P4148 简单题 - KDT
你有一个\(N \times N\)的棋盘,每个格子内有一个整数,初始时的时候全部为 \(0\),现在需要维护两种操作:
1 x y A\(1\le x,y\le N\),\(A\) 是正整数。将格子x,y里的数字加上 \(A\)。2 x1 y1 x2 y2\(1 \le x_1 \le x_2 \le N\),\(1 \le y_1\le y_2 \le N\)。输出 \(x_1, y_1, x_2, y_2\) 这个矩形内的数字和3无 终止程序\(1\leq N\leq 5\times 10^5\),操作数不超过 \(2\times 10^5\) 个,内存限制 \(20\texttt{MB}\),保证答案在 int 范围内并且解码之后数据仍合法。
对于这种二维问题很容易想到直接用 KDT 解决,
每次加点,如果不平衡就直接暴力重构即可。(不太会证时间,lxl 说单次是 \(\mathcal O(n ^{\frac{2}{3}})\) 的)
#include <bits/stdc++.h>
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
void prt(int x){
int P[15],tmp=0;
if(x==0) putchar('0');
if(x<0) putchar('-'),x=-x;
while(x) P[++tmp]=x%10,x/=10;
for(int i=tmp;i>=1;i--) putchar(P[i]+'0');
putchar('\n');
}
const int N=5e5+5;
int n,idx,KD,tp=0,q[N],rt,lst;
struct node{
int x[2],w;
friend bool operator <(node x,node y) {return x.x[KD]<y.x[KD];}
}a[N];
struct KDT{
int s,sz,lc,rc,mn[2],mx[2];
node nw;
}tr[N];
int nwnode(){
if(tp) return q[tp--];
return ++idx;
}
#define lc(p) tr[p].lc
#define rc(p) tr[p].rc
void pu(int p){
tr[p].s=tr[lc(p)].s+tr[rc(p)].s+tr[p].nw.w;
tr[p].sz=tr[lc(p)].sz+tr[rc(p)].sz+1;
for(int i=0;i<2;i++){
tr[p].mn[i]=tr[p].mx[i]=tr[p].nw.x[i];
if(lc(p)) tr[p].mn[i]=min(tr[p].mn[i],tr[lc(p)].mn[i]),tr[p].mx[i]=max(tr[p].mx[i],tr[lc(p)].mx[i]);
if(rc(p)) tr[p].mn[i]=min(tr[p].mn[i],tr[rc(p)].mn[i]),tr[p].mx[i]=max(tr[p].mx[i],tr[rc(p)].mx[i]);
}
}
int build(int l,int r,int kd){
if(l>r) return 0;
int mid=((l+r)>>1),p=nwnode();
KD=kd,nth_element(a+l,a+mid,a+r+1);
tr[p].nw=a[mid];
tr[p].lc=build(l,mid-1,kd^1);
tr[p].rc=build(mid+1,r,kd^1);
pu(p);return p;
}
void pia(int p,int num){
if(lc(p)) pia(lc(p),num);
a[tr[lc(p)].sz+num+1]=tr[p].nw;
if(rc(p)) pia(rc(p),tr[lc(p)].sz+num+1);
}
void chk(int &p,int kd){
if(0.75*tr[p].sz<1.0*tr[lc(p)].sz||0.75*tr[p].sz<1.0*tr[rc(p)].sz) pia(p,0),p=build(1,tr[p].sz,kd);
}
void ins(int &p,node nw,int kd){
if(!p){
p=nwnode();
tr[p].lc=tr[p].rc=0;
tr[p].nw=nw;pu(p);
return;
}
if(nw.x[kd]<=tr[p].nw.x[kd]) ins(lc(p),nw,kd^1);
else ins(rc(p),nw,kd^1);
pu(p);chk(p,kd);
}
bool in(int p,int x1,int y1,int x2,int y2){
return tr[p].mn[0]>=x1&&tr[p].mx[0]<=x2&&tr[p].mn[1]>=y1&&tr[p].mx[1]<=y2;
}
bool out(int p,int x1,int y1,int x2,int y2){
return tr[p].mn[0]>x2||tr[p].mx[0]<x1||tr[p].mn[1]>y2||tr[p].mx[1]<y1;
}
int qry(int p,int x1,int y1,int x2,int y2){
if(out(p,x1,y1,x2,y2)) return 0;
if(in(p,x1,y1,x2,y2)) return tr[p].s;
int res=0;
if(tr[p].nw.x[0]>=x1&&tr[p].nw.x[0]<=x2&&tr[p].nw.x[1]>=y1&&tr[p].nw.x[1]<=y2) res+=tr[p].nw.w;
res+=qry(lc(p),x1,y1,x2,y2)+qry(rc(p),x1,y1,x2,y2);
return res;
}
int main(){
/*2023.12.28 H_W_Y P4148 简单题 KDT*/
n=read();
while(1){
int op,x1,x2,y1,y2;
cin>>op;if(op==3) break;
if(op==1) ins(rt,(node){read()^lst,read()^lst,read()^lst},0);
else{
cin>>x1>>y1>>x2>>y2;x1^=lst,x2^=lst,y1^=lst,y2^=lst;
lst=qry(rt,x1,y1,x2,y2);prt(lst);
}
}
return 0;
}
P7834 Peaks - Kruskal 重构树 + 主席树
给定一张 \(n\) 个点、\(m\) 条边的无向图,第 \(i\) 个点的权值为 \(a_i\),边有边权。
有 \(q\) 组询问,每组询问给定三个整数 \(u, x, k\),求从 \(u\) 开始只经过权值 \(\leq x\) 的边所能到达的权值第 \(k\) 大的点的权值,如果不存在输出 \(-1\)。
本题强制在线。
\(1 \leq n \leq 10^5\),\(0 \leq m, q \leq 5 \times 10^5\),\(1 \leq s, t \leq n\),\(1 \leq a_i, w \leq 10^9\),\(0 \leq u', x', k' < 2^{31}\)。
首先不难想到用 Kruskal 重构树,
而又因为强制在线,有要求第 \(k\) 大,于是直接维护一棵主席树就做完了。
注意 inf 的取值,取不到那么大就需要判断一下!
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
const int N=5e5+5,inf=2e9;
int n,m,q,a[N],rt[N],fa[N],idx=0,cnt=0,lst=0,val[N],b[N],len,f[N][22],rev[N],dfn[N],ed[N];
struct edge{
int u,v,w;
bool operator <(const edge &rhs) const{return w<rhs.w;}
}e[N];
vector<int> g[N];
int find(int x){return (x==fa[x])?x:fa[x]=find(fa[x]);}
void merge(int u,int v,int w){
u=find(u);v=find(v);
if(u==v) return;
val[++cnt]=w;
g[cnt].pb(u);g[cnt].pb(v);
fa[u]=fa[v]=cnt;
}
namespace SGT{
struct sgt{int v,s[2];}tr[N*23];
int cnt=0;
#define mid ((l+r)>>1)
#define lc(p) tr[p].s[0]
#define rc(p) tr[p].s[1]
void pu(int p){tr[p].v=tr[lc(p)].v+tr[rc(p)].v;}
void build(int &p,int l,int r){
p=++cnt;tr[p].v=0;
if(l==r) return ;
build(lc(p),l,mid);build(rc(p),mid+1,r);
}
void upd(int &p,int pre,int l,int r,int x,int v){
p=++cnt;tr[p]=tr[pre];
if(l==r) return tr[p].v+=v,void();
if(x<=mid) upd(lc(p),lc(pre),l,mid,x,v);
else upd(rc(p),rc(pre),mid+1,r,x,v);pu(p);
}
int qry(int p,int pre,int l,int r,int k){
if(l==r) return l;
if(tr[p].v-tr[pre].v<k) return -1;
if(rc(p)&&tr[rc(p)].v-tr[rc(pre)].v>=k) return qry(rc(p),rc(pre),mid+1,r,k);
return qry(lc(p),lc(pre),l,mid,k-tr[rc(p)].v+tr[rc(pre)].v);
}
}
void dfs(int u,int FA){
dfn[u]=++idx;rev[idx]=u;
f[u][0]=FA;
for(int i=1;i<=20;i++) f[u][i]=f[f[u][i-1]][i-1];
for(auto v:g[u]) dfs(v,u);
ed[u]=idx;
}
int main(){
/*2023.12.27 H_W_Y P7834 [ONTAK2010] Peaks 加强版 Kruskal 重构树 + 主席树*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m>>q;cnt=n;val[0]=inf;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i];
sort(b+1,b+n+1);len=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+len+1,a[i])-b;
for(int i=1;i<=m;i++) cin>>e[i].u>>e[i].v>>e[i].w;
sort(e+1,e+m+1);
for(int i=1;i<=n*2;i++) fa[i]=i;
for(int i=1;i<=m;i++) merge(e[i].u,e[i].v,e[i].w);
for(int i=1;i<=cnt;i++) if(find(i)==i) dfs(i,0);
SGT::build(rt[0],0,len);
for(int i=1;i<=cnt;i++) SGT::upd(rt[i],rt[i-1],0,len,a[rev[i]],1);
lst=0;
for(int u,x,k;q;q--){
cin>>u>>x>>k;
u=(u^lst)%n+1;k=(k^lst)%n+1;x=x^lst;
for(int i=20;i>=0;i--) if(f[u][i]&&val[f[u][i]]<=x) u=f[u][i];//记得判断 f[u][i]
lst=b[SGT::qry(rt[ed[u]],rt[dfn[u]-1],0,len,k)];
if(!lst) cout<<"-1\n";
else cout<<lst<<'\n';
}
return 0;
}
P4751 DDP(加强版)
如何优化 DDP?不想建全局平衡二叉树
直接把每一条重链拉出来建立一棵线段树即可——
这个优化效果真的很好。
#include <bits/stdc++.h>
using namespace std;
#define mid ((l+r)>>1)
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
void prt(int x){
int P[15],tmp=0;
if(x==0) putchar('0');
if(x<0) putchar('-'),x=-x;
while(x) P[++tmp]=x%10,x/=10;
for(int i=tmp;i>=1;--i) putchar(P[i]+'0');
putchar('\n');
}
int min(int x,int y){return x<y?x:y;}
int max(int x,int y){return x<y?y:x;}
const int N=1e6+5,inf=0x3f3f3f3f;
int n,m,head[N],tot=0,a[N],son[N],id[N],rev[N],fa[N],f[N][2],top[N],dep[N],siz[N],ed[N],idx=0,lst=0;
int rt[N],lc[N<<2],rc[N<<2],cnt=0;
struct edge{
int v,nxt;
}e[N<<1];
struct matrix{
int g[2][2];
matrix(){memset(g,0,sizeof(g));}
matrix operator *(const matrix &a) const{
matrix res;
res.g[0][0]=max(g[0][1]+a.g[1][0],g[0][0]+a.g[0][0]);
res.g[0][1]=max(g[0][1]+a.g[1][1],g[0][0]+a.g[0][1]);
res.g[1][0]=max(g[1][1]+a.g[1][0],g[1][0]+a.g[0][0]);
res.g[1][1]=max(g[1][1]+a.g[1][1],g[1][0]+a.g[0][1]);
return res;
}
}tr[N<<2],g[N];
void add(int u,int v){
e[++tot]=(edge){v,head[u]};
head[u]=tot;
e[++tot]=(edge){u,head[v]};
head[v]=tot;
}
void dfs1(int u,int pre){
fa[u]=pre,dep[u]=dep[pre]+1;son[u]=-1;siz[u]=1;
f[u][1]=a[u];
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==pre) continue;
dfs1(v,u);
siz[u]+=siz[v];
f[u][1]+=f[v][0];
f[u][0]+=max(f[v][0],f[v][1]);
if(son[u]==-1||siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int pre){
top[u]=pre;id[u]=++idx;rev[idx]=u;ed[pre]=idx;
g[u].g[1][0]=a[u];
g[u].g[1][1]=-inf;
if(son[u]==-1) return;
dfs2(son[u],pre);
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa[u]||v==son[u]) continue;
dfs2(v,v);
g[u].g[0][0]+=max(f[v][0],f[v][1]);
g[u].g[1][0]+=f[v][0];
}
g[u].g[0][1]=g[u].g[0][0];
}
void pu(int p){tr[p]=tr[lc[p]]*tr[rc[p]];}
void build(int l,int r,int &p){
p=++cnt;
if(l==r){
tr[p]=g[rev[l]];
return;
}
build(l,mid,lc[p]);build(mid+1,r,rc[p]);pu(p);
}
matrix query(int l,int r,int p,int x,int y){
if(x<=l&&y>=r) return tr[p];
if(y<=mid) return query(l,mid,lc[p],x,y);
if(x>mid) return query(mid+1,r,rc[p],x,y);
return query(l,mid,lc[p],x,y)*query(mid+1,r,rc[p],x,y);
}
void update(int l,int r,int p,int x){
if(l==r){
tr[p]=g[rev[l]];
return ;
}
(x<=mid)?update(l,mid,lc[p],x):update(mid+1,r,rc[p],x);pu(p);
}
void upd(int u,int val){
g[u].g[1][0]+=val-a[u];
a[u]=val;
while(u){
matrix lst=tr[rt[top[u]]];
update(id[top[u]],ed[top[u]],rt[top[u]],id[u]);
matrix nw=tr[rt[top[u]]];
u=fa[top[u]];
g[u].g[0][0]+=max(nw.g[0][0],nw.g[1][0])-max(lst.g[0][0],lst.g[1][0]);
g[u].g[1][0]+=nw.g[0][0]-lst.g[0][0];
g[u].g[0][1]=g[u].g[0][0];
}
}
int main(){
/*2023.9.11 H_W_Y P4719 【模板】"动态 DP"&动态树分治 动态 dp*/
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1,u,v;i<n;i++){
u=read();v=read();
add(u,v);
}
dfs1(1,0);dfs2(1,1);
for(int i=1;i<=n;i++) if(top[i]==i) build(id[i],ed[i],rt[i]);
for(int i=1,u,val;i<=m;i++){
u=read();val=read();u^=lst;
upd(u,val);
matrix ans=tr[rt[1]];
prt((lst=max(ans.g[0][0],ans.g[1][0])));
}
return 0;
}
P5327 语言 - 线段树合并 + 树上差分
逐渐离谱——不是还有一个树上问题专题啊,怎么 DS 就要讲完了。
在一个遥远的国度,有 \(n\) 个城市。城市之间有 \(n - 1\) 条双向道路,这些道路保证了任何两个城市之间都能直接或者间接地到达。
在上古时代,这 \(n\) 个城市之间处于战争状态。在高度闭塞的环境中,每个城市都发展出了自己的语言。而在王国统一之后,语言不通给王国的发展带来了极大的阻碍。为了改善这种情况,国王下令设计了 \(m\) 种通用语,并进行了 \(m\) 次语言统一工作。在第 \(i\) 次统一工作中,一名大臣从城市 \(s_i\) 出发,沿着最短的路径走到了 \(t_i\),教会了沿途所有城市(包括 \(s_i, t_i\))使用第 \(i\) 个通用语。
一旦有了共通的语言,那么城市之间就可以开展贸易活动了。两个城市 \(u_i, v_i\) 之间可以开展贸易活动当且仅当存在一种通用语 \(L\) 满足 \(u_i\) 到 \(v_i\) 最短路上的所有城市(包括 \(u_i, v_i\)),都会使用 \(L\)。
为了衡量语言统一工作的效果,国王想让你计算有多少对城市 \((u, v)\)(\(u < v\)),他们之间可以开展贸易活动。
\(1 \le x_i, y_i, s_i, t_i \le n\leq 10 ^ 5\),\(1\leq m\leq 10 ^ 5\),\(x_i\neq y_i\)。
很有意思的一道题目。
对于每一个点,我们还是考虑它的贡献,可以是能贸易的也可以是不能贸易的。
但是分析一下发现可以贸易的构成了一个连动块,所以我们肯定是来算它了。
而连动块计数怎么完成呢?
不难想到它的边界点一定是这些 \(s,t\),
于是我们可以通过 \(s,t\) 构成了一个连动块的所有边界点,
而按照 dfn 序排序之后,设当前点是 \(u\),它加入连动块的贡献就是 \(dep[u]-dep[lca(u,v)]\),其中 \(v\) 是上一个加入的点。
这是容易证明的,用 dfn 求 LCA 的时候就用到了这个特点,
最开始我们强制 \(1\) 选,最后再减去 \(dep[lca(L,R)]\) 即可,\(L,R\) 是 dfn 最大和最小的点。
发现这个东西可以直接用线段树维护,
而要求所有点就容易先到用线段树合并。
因为每一次我们是先解决了子树问题再到 \(u\) 节点的,
所以我们似乎可以直接用树上差分来解决问题,即在 \((s,t)\) 路径的 \(s,t\) 处加,在 \(lca,fa[lca]\) 处减去即可。
这样就做完了,而代码实现是简单的,重要的就是分析的过程。
#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define ll long long
const int N=2e5+5;
int n,m,dep[N],st[20][N],lg[N],dfn[N],idx=0,rt[N],f[N];
vector<int> g[N],del[N];
ll ans=0;
void dfs(int u,int fa){
dfn[u]=++idx;dep[u]=dep[fa]+1;st[0][idx]=fa;f[u]=fa;
for(auto v:g[u]) if(v!=fa) dfs(v,u);
}
int Min(int u,int v){return dfn[u]<dfn[v]?u:v;}
void init(){
lg[1]=0;dfs(1,0);
for(int i=2;i<=n;i++) lg[i]=lg[i/2]+1;
for(int i=1;i<=lg[n]+1;i++)
for(int j=1;j+(1<<i)-1<=n;j++)
st[i][j]=Min(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}
int LCA(int u,int v){
if(!u||!v) return 0;
u=dfn[u];v=dfn[v];
if(u>v) swap(u,v);
int s=lg[v-u];
return Min(st[s][u+1],st[s][v-(1<<s)+1]);
}
struct SGT{
struct sgt{int s[2],lx,rx,v,c;}tr[N*50];
int idx=0;
#define mid ((l+r)>>1)
#define lc(p) tr[p].s[0]
#define rc(p) tr[p].s[1]
void pu(int p){
int L=lc(p),R=rc(p);
tr[p].v=tr[L].v+tr[R].v-dep[LCA(tr[L].rx,tr[R].lx)];
tr[p].lx=tr[L].lx?tr[L].lx:tr[R].lx;
tr[p].rx=tr[R].rx?tr[R].rx:tr[L].rx;
}
void upd(int &p,int l,int r,int x,int v){
if(!p) p=++idx;
if(l==r){
tr[p].c+=v;
tr[p].v=tr[p].c?dep[x]:0;
tr[p].lx=tr[p].rx=tr[p].c?x:0;
return;
}
(dfn[x]<=mid)?upd(lc(p),l,mid,x,v):upd(rc(p),mid+1,r,x,v);pu(p);
}
int qry(int p){return tr[p].v-dep[LCA(tr[p].lx,tr[p].rx)];}
int merge(int p1,int p2,int l,int r){
if(!p1||!p2) return p1+p2;
if(l==r){
tr[p1].c+=tr[p2].c;tr[p1].v|=tr[p2].v;tr[p1].lx|=tr[p2].lx,tr[p1].rx|=tr[p2].rx;
return p1;
}
lc(p1)=merge(lc(p1),lc(p2),l,mid);
rc(p1)=merge(rc(p1),rc(p2),mid+1,r);
pu(p1);return p1;
}
}T;
void sol(int u){
for(auto v:g[u]) if(v!=f[u]) sol(v);
for(auto v:del[u]) T.upd(rt[u],1,n,v,-1);
ans+=T.qry(rt[u]);rt[f[u]]=T.merge(rt[f[u]],rt[u],1,n);
}
int main(){
/*2023.12.28 H_W_Y P5327 [ZJOI2019] 语言 线段树合并*/
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i=1,u,v;i<n;i++) cin>>u>>v,g[u].pb(v),g[v].pb(u);
init();
for(int i=1,u,v,lca;i<=m;i++){
cin>>u>>v;lca=LCA(u,v);
T.upd(rt[u],1,n,u,1);T.upd(rt[u],1,n,v,1);
T.upd(rt[v],1,n,u,1);T.upd(rt[v],1,n,v,1);
del[lca].pb(u);del[lca].pb(v);del[f[lca]].pb(u);del[f[lca]].pb(v);
}
sol(1);cout<<(ans>>1)<<'\n';
return 0;
}
Conclusion
- 对于求 \(k\) 小/大值的题目可以考虑直接 整体二分。(P1527 [国家集训队] 矩阵乘法,P4175 [CTSC2008] 网络管理)
- 有关求路径/LCA 的问题,我们还是都把他转化到深度上面,最后讨论一下 LCA 的位置即可。(P5210 [ZJOI2017] 线段树)
- 线段树的区间操作可以考虑 zkw 线段树的处理方式。(P5210 [ZJOI2017] 线段树)
- 线段树区间修改的标记下传问题可以考虑分五类节点讨论,去维护每个节点被打标记的概率。(P5280 [ZJOI2019] 线段树)
- 树上维护子树外的点可以先将所有点加入集合,再进行一次遍历逐渐删去子树中的点。(CF768G The Winds of Winter)
- 区间子区间的问题只涉及差分就可以直接用树状数组维护,注意会多一个数组记录减去的值。(P3722 [AH2017/HNOI2017] 影魔)
- inf 一定要取足够大,\(2^{31} \gt 2\times 10^9\)!!!(P7834 [ONTAK2010] Peaks 加强版)
- 子树的问题可以先把 dfn 序求出来再来维护,不需要在树上 dfs 的时候就维护出来。(P7834 [ONTAK2010] Peaks 加强版)
- 求 \(u,v\) 之间的边权最大异或和其实就是用任意的 \(dis_{u,v} \oplus\) 图中每条边的所在的任意环即可。(P3733 [HAOI2017] 八纵八横)
- 维护可删除线性基可以直接 离线 下来保证 \(i\) 位的删除时间最晚。(P3733 [HAOI2017] 八纵八横)
- 有关在哪一个点取最值的题目我们可以把它转化成 函数,在图像上面分析规律。(P3642 [APIO2016] 烟火表演)
- 二维加点问题可以直接用 KDT 解决,注意在不平衡时直接暴力重构即可。(P4148 简单题)
- 树上连动块大小计数问题,可以直接维护 最远点,用 LCA 和 dep 来计算贡献。(P5327 [ZJOI2019] 语言)
- 树剖 + 线段树的优化——每一条重链拉出来分别建一棵线段树。(P4751 【模板】"动态DP"&动态树分治(加强版))
- 树上的颜色段均摊问题直接对于每一种颜色维护 \(st\) 和 \(ed\),接着不断往上面跳颜色段即可。(P3703 [SDOI2017] 树点涂色)
- 树形 dp 需要优化的时候都可以考虑用 线段树合并 去完成。(P6773 [NOI2020] 命运)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号