2.1937.Codeforces Round 930 (Div. 2) - sol2024-03-01

3.1934.Codeforces Round 931 (Div. 2) - sol2024-03-03 4.1935.Codeforces Round 932 (Div. 2) - sol2024-03-06 5.1938.2024 ICPC Asia Pacific Championship - sol2024-03-08 6.1948.Educational Codeforces Round 163 - sol2024-03-19 7.1943+1944.Codeforces Round 934 (Div. 1,Div. 2) - sol2024-03-21

20240301

由于笔者实力较弱，所以这只是 Div 2 的题解。

四年一次的比赛啊，还是要打。

Dashboard - Codeforces Round 930 (Div. 2) - Codeforces

A. Shuffle Party

You are given an array $a_{1}, a_{2}, \dots, a_{n}$ . Initially, $a_{i} = i$ for each $1 \leq i \leq n$ .

The operation $swap (k)$ for an integer $k \geq 2$ is defined as follows:

Let $d$ be the largest divisor $^{†}$ of $k$ which is not equal to $k$ itself. Then swap the elements $a_{d}$ and $a_{k}$ .

Suppose you perform $swap (i)$ for each $i = 2, 3, \dots, n$ in this exact order. Find the position of $1$ in the resulting array. In other words, find such $j$ that $a_{j} = 1$ after performing these operations.

$^{†}$ An integer $x$ is a divisor of $y$ if there exists an integer $z$ such that $y = x \cdot z$ .

$1 \leq n \leq 10^{9}$ 。

容易发现，换到的位置都是 $2$ 的幂次，所以直接枚举一下最大的幂次即可。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=2e5+5;
int n,T;

void sol(){
  cin>>n;
  for(int i=30;i>=0;i--) if(n>=(1<<i)){cout<<(1<<i)<<'\n';break;}
}

int main(){
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>T;
  while(T--) sol();
  return 0;
}

B. Binary Path

You are given a $2 \times n$ grid filled with zeros and ones. Let the number at the intersection of the $i$ -th row and the $j$ -th column be $a_{i j}$ .

There is a grasshopper at the top-left cell $(1, 1)$ that can only jump one cell right or downwards. It wants to reach the bottom-right cell $(2, n)$ . Consider the binary string of length $n + 1$ consisting of numbers written in cells of the path without changing their order.

Your goal is to:

Find the lexicographically smallest $^{†}$ string you can attain by choosing any available path;

Find the number of paths that yield this lexicographically smallest string.

$^{†}$ If two strings $s$ and $t$ have the same length, then $s$ is lexicographically smaller than $t$ if and only if in the first position where $s$ and $t$ differ, the string $s$ has a smaller element than the corresponding element in $t$ .

$2 \leq n \leq 2 \times 10^{5}$ 。

由于每一次只能往下和往右，所以其实我们只需要找到一个中断点，从这个点往下走即可。

而第一次找到的路径我们一定希望越远越好，也就是一直往右走，知道有一个位置右边是 $1$ 下面是 $0$ 位置。

这样我们就可以轻松找到最短的序列。

再来考虑出现次数，容易想到画图去解决问题。

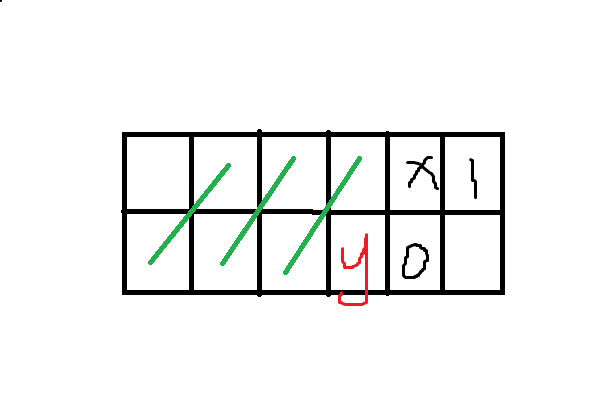
假设我们在 $x$ 这个地方下来，那么可能的情况一定是在 $x$ 之前就走下来。

如果 $x = y$ 则我们就可以从 $y$ 上面的位置下来，同理，对于每一条绿线，我们都去比较是否可行，如果不等就直接 break，因为一个不等之后就不会再成立了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long

const int N=2e5+5;
int n,T,tmp=0;
string s[2];

void sol(){
  cin>>n>>s[0]>>s[1];
  for(int i=0;i<n;i++){
    cout<<s[0][i];
    if(i<n-1&&s[0][i+1]=='0') continue;
    if(i<n-1&&s[0][i+1]==s[1][i]) continue;
    tmp=i;break;
  }
  for(int i=tmp;i<n;i++) cout<<s[1][i];
  cout<<'\n';
  int cnt=1;
  for(int i=tmp;i>0;i--){
    if(s[0][i]==s[1][i-1]) ++cnt;
    else break;
  }
  cout<<cnt<<'\n';
}

int main(){
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>T;
  while(T--) sol();
  return 0;
}

C. Bitwise Operation Wizard

This is an interactive problem.

There is a secret sequence $p_{0}, p_{1}, \dots, p_{n - 1}$ , which is a permutation of ${0, 1, \dots, n - 1}$ .

You need to find any two indices $i$ and $j$ such that $p_{i} \oplus p_{j}$ is maximized, where $\oplus$ denotes the bitwise XOR operation.

To do this, you can ask queries. Each query has the following form: you pick arbitrary indices $a$ , $b$ , $c$ , and $d$ ( $0 \leq a, b, c, d < n$ ). Next, the jury calculates $x = (p_{a} ∣ p_{b})$ and $y = (p_{c} ∣ p_{d})$ , where $|$ denotes the bitwise OR operation. Finally, you receive the result of comparison between $x$ and $y$ . In other words, you are told if $x < y$ , $x > y$ , or $x = y$ .

Please find any two indices $i$ and $j$ ( $0 \leq i, j < n$ ) such that $p_{i} \oplus p_{j}$ is maximum among all such pairs, using at most $3 n$ queries. If there are multiple pairs of indices satisfying the condition, you may output any one of them.

$1 \leq n \leq 10^{4}$ 。

场上不会 C 的小丑。

发现直接讨论两个数是非常不好做的，所以我们可以一个一个来。

考虑我们可以通过 $O (n)$ 次询问找到 $n - 1$ ，每次询问都是通过 $a, a, b, b$ 的形式，

而在答案中选 $n - 1$ 一定是不劣的。

进一步，我们可以通过与 $n - 1$ 的或来找到一些与 $n - 1$ 或起来最大的数 $i d []$ ，这些数满足他们在 $n - 1$ 为 $0$ 的位置一定为 $1$ ，

而异或中，我们还要求 $n - 1$ 为 $1$ 的位置不能为 $1$ ，所以我们再在这些数中找到最小的那个就可以了。

后两次的操作也都可以在 $O (n)$ 次询问内完成，于是我们就做完了。

#include <bits/stdc++.h>
using namespace std;

const int N=1e5+5;
int id[N],tmp1,tmp2,cnt=0,n,T;
char ch;

void sol(){
  scanf("%d",&n);
  tmp1=cnt=0;tmp2=-1;
  for(int i=1;i<n;i++){
  	printf("? %d %d %d %d\n",tmp1,tmp1,i,i);
  	fflush(stdout);
  	ch=getchar();
  	while(ch!='='&&ch!='<'&&ch!='>') ch=getchar();
  	if(ch=='<') tmp1=i; 
  }
  for(int i=0;i<n;i++){
    if(i==tmp1) continue;
    if(!cnt){id[++cnt]=i;continue;}
    printf("? %d %d %d %d\n",tmp1,id[cnt],tmp1,i);
    fflush(stdout);
    ch=getchar();
    while(ch!='='&&ch!='<'&&ch!='>') ch=getchar();
    if(ch=='<') id[cnt=1]=i;
    else if(ch=='=') id[++cnt]=i;
  }
  tmp2=id[1];
  for(int i=2;i<=cnt;i++){
    printf("? %d %d %d %d\n",tmp2,tmp2,id[i],id[i]);
    fflush(stdout);
    ch=getchar();
    while(ch!='='&&ch!='<'&&ch!='>') ch=getchar();
    if(ch=='>') tmp2=id[i];
  }
  printf("! %d %d\n",tmp1,tmp2);
  fflush(stdout);
}

int main(){
  scanf("%d",&T);
  while(T--) sol();
  return 0;
}

D. Pinball

There is a one-dimensional grid of length $n$ . The $i$ -th cell of the grid contains a character $s_{i}$ , which is either '<' or '>'.

When a pinball is placed on one of the cells, it moves according to the following rules:

If the pinball is on the $i$ -th cell and $s_{i}$ is '<', the pinball moves one cell to the left in the next second. If $s_{i}$ is '>', it moves one cell to the right.

After the pinball has moved, the character $s_{i}$ is inverted (i. e. if $s_{i}$ used to be '<', it becomes '>', and vice versa).

The pinball stops moving when it leaves the grid: either from the left border or from the right one.

You need to answer $n$ independent queries. In the $i$ -th query, a pinball will be placed on the $i$ -th cell. Note that we always place a pinball on the initial grid.

For each query, calculate how many seconds it takes the pinball to leave the grid. It can be shown that the pinball will always leave the grid within a finite number of steps.

$1 \leq n \leq 5 \times 10^{5}$ 。

这是一道简单题，主要就是去手玩一下走的过程。

建议自己多画几个样例，把走的路线画出来就知道怎么做了。

（不想写了，感觉也比较难以描述。）

#include <bits/stdc++.h>
using namespace std;
#define int long long

const int N=5e5+5;
int n,T,c[2],S[2][N],d[2][N];
char s[N];

int calc(int l,int r,int op){return S[op][r]-S[op][l-1];}

void sol(){
  scanf("%lld%s",&n,s+1);c[0]=c[1]=0;
  for(int i=1;i<=n;i++){
    if(s[i]=='>') ++c[0],S[0][c[0]]=S[0][c[0]-1]+i*2;
    else ++c[1],S[1][c[1]]=S[1][c[1]-1]+i*2;
    d[0][i]=c[0],d[1][i]=c[1];
  }
  for(int i=1;i<=n;i++){
    if(s[i]=='>'){
      if(d[0][i]>c[1]-d[1][i]) printf("%lld ",calc(d[1][i]+1,c[1],1)-calc(d[0][i]-(c[1]-d[1][i]),d[0][i],0)+i+n+1);
      else printf("%lld ",calc(d[1][i]+1,d[1][i]+d[0][i],1)-calc(1,d[0][i],0)+i);
    }else{
      if(d[0][i]<c[1]-d[1][i]+1) printf("%lld ",calc(d[1][i],d[1][i]+d[0][i],1)-calc(1,d[0][i],0)-i);
      else printf("%lld ",calc(d[1][i],c[1],1)-i-calc(d[0][i]-(c[1]-d[1][i]),d[0][i],0)+n+1);
    }
  }
  printf("\n");
}

signed main(){
  scanf("%lld",&T);
  while(T--) sol();
  return 0;
}

E. Pokémon Arena

You are at a dueling arena. You also possess $n$ Pokémons. Initially, only the $1$ -st Pokémon is standing in the arena.

Each Pokémon has $m$ attributes. The $j$ -th attribute of the $i$ -th Pokémon is $a_{i, j}$ . Each Pokémon also has a cost to be hired: the $i$ -th Pokémon's cost is $c_{i}$ .

You want to have the $n$ -th Pokémon stand in the arena. To do that, you can perform the following two types of operations any number of times in any order:

Choose three integers $i$ , $j$ , $k$ ( $1 \leq i \leq n$ , $1 \leq j \leq m$ , $k > 0$ ), increase $a_{i, j}$ by $k$ permanently. The cost of this operation is $k$ .

Choose two integers $i$ , $j$ ( $1 \leq i \leq n$ , $1 \leq j \leq m$ ) and hire the $i$ -th Pokémon to duel with the current Pokémon in the arena based on the $j$ -th attribute. The $i$ -th Pokémon will win if $a_{i, j}$ is greater than or equal to the $j$ -th attribute of the current Pokémon in the arena (otherwise, it will lose). After the duel, only the winner will stand in the arena. The cost of this operation is $c_{i}$ .

Find the minimum cost you need to pay to have the $n$ -th Pokémon stand in the arena.

$1 \leq n \times m \leq 4 \times 10^{5}$ 。

图论好题。

首先， $O (n^{2} m)$ 的建图方法是简单的，现在我们考虑如何优化。

分析一下，考虑这样一种建图方式，对于每一个属性，我们都建立出 $2 n$ 个点，还有 $n$ 个点为那 $n$ 个点本身。

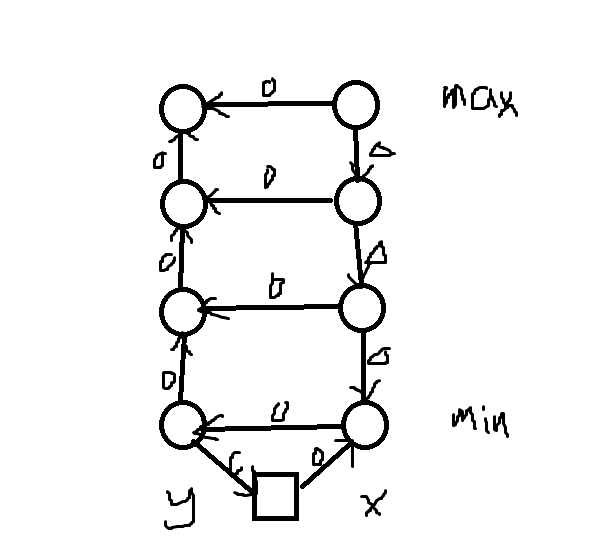
我们的两列点都是按照从大到小的顺序做的。

可以模拟一下，发现这样就变成了求 $1 \sim n$ 的最短路了。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define fi first
#define se second

const int N=2e6+5;
const ll inf=1e18;
int n,m,c[N],idx=0,T;
ll dis[N];
vector<pair<int,ll>> G[N];
bool vis[N];

struct node{
  int id,v;
  bool operator <(const node &rhs) const{return v<rhs.v;}
};
vector<node> a[N];

ll dij(){
  for(int i=1;i<=idx;i++) dis[i]=inf,vis[i]=false;
  dis[1]=0;
  priority_queue<pair<ll,int> > Q;
  Q.push({0,1});
  while(!Q.empty()){
    int u=Q.top().se;Q.pop();
    if(vis[u]) continue;
    vis[u]=true;
    for(auto i:G[u]){
      ll w=i.se,v=i.fi;
      if(dis[v]>dis[u]+w){
      	dis[v]=dis[u]+w;
      	Q.push({-dis[v],v});
      }
    }
  }
  return dis[n];
}

void sol(){
  cin>>n>>m;idx=n;
  for(int i=1;i<=n;i++) cin>>c[i];
  for(int i=1;i<=n;i++) for(int j=1,x;j<=m;j++) cin>>x,a[j].pb((node){i,x});
  for(int i=1;i<=m;i++){
  	sort(a[i].begin(),a[i].end());
  	for(int j=1;j<=n;j++) G[j].pb({idx+j,0}),G[idx+n+j].pb({j,c[j]}),G[idx+j].pb({idx+n+j,0});
  	for(int j=1;j<n;j++) G[idx+a[i][j].id].pb({idx+a[i][j-1].id,a[i][j].v-a[i][j-1].v});
  	for(int j=0;j+1<n;j++) G[idx+n+a[i][j].id].pb({idx+n+a[i][j+1].id,0});
  	idx+=2*n;a[i].clear();
  }
  cout<<dij()<<'\n';
  for(int i=1;i<=idx;i++) G[i].clear();
}

int main(){
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>T;
  while(T--) sol();
  return 0;
}

F. Bitwise Paradox

You are given two arrays $a$ and $b$ of size $n$ along with a fixed integer $v$ .

An interval $[l, r]$ is called a good interval if $(b_{l} ∣ b_{l + 1} ∣ \dots ∣ b_{r}) \geq v$ , where $|$ denotes the bitwise OR operation. The beauty of a good interval is defined as $max (a_{l}, a_{l + 1}, \dots, a_{r})$ .

You are given $q$ queries of two types:

"1 i x": assign $b_{i} := x$ ;

"2 l r": find the minimum beauty among all good intervals $[l_{0}, r_{0}]$ satisfying $l \leq l_{0} \leq r_{0} \leq r$ . If there is no suitable good interval, output $- 1$ instead.

Please process all queries.

$1 \leq n, q \leq 2 \times 10^{5}, 1 \leq a_{i}, b_{i} \leq 10^{9}$ 。

DS 好题。一篇认认真真的题解（~~上面的几道题都不认真~~）。

读完题目，发现这是一个与二进制相关的问题，

而容易发现，每组数据中 $v, a_{i}$ 都是不变的，且涉及到 $b_{l} | b_{l + 1} | \dots | b_{r} \geq v$ 的计算，

我们不难想到拆位，也就是对每一个二进制位分开来讨论。

现在再来看数据范围，直觉是可以去尝试 Poly log 的做法，

而用最普通的线段树来维护，问题就在于我们如何去 合并两个区间。

发现这是好做的，我们同样按照二进制位从高到低考虑，合并区间 $[l, m i d]$ 和 $[m i d + 1, r]$ ，得到最优的满足条件区间 $[L, R]$ 。

设当前枚举到第 $i$ 位，假设 $v$ 的这一位要求是 $1$ ，那么这个 $1$ 一定来源于左区间或者右区间（根据或运算）。

假设左区间从右往左第一个 $i$ 位为 $1$ 的位置是 $P$ ，右区间从左往右第一个 $i$ 位为 $1$ 的位置是 $Q$ ，则：

如果 ${max}_{i = P}^{m i d} a_{i} \leq {max}_{i = m i d + 1}^{Q} a_{i}$ ，那么我们选择把 $L$ 扩展到 $P$ 。
反之我们选择把 $R$ 拓展到 $Q$ 。

这样贪心地选择一定是不劣的，因为你总需要拓展一个，我们希望答案尽可能优。

而 $v$ 的这一位不要求为 $1$ 的情况也是简单的，我们枚举选还是不选：

如果把这一位选成 $1$ ，操作与上面相同，而后面的位我们都不用选了，这样直接算上此时区间最大值与答案取 $min$ 。
不选则继续往下枚举。

这样我们就可以做到两个区间的合并了，

实现中只需要维护一个区间每一位的 $P, Q$ ，容易发现这也是好维护的，下面是区间合并的代码：

  //S(l,r) 算区间 [l,r] 中 a_i 的最大值
  sgt operator +(sgt Lp,sgt Rp){//合并区间 Lp 和 Rp
  	sgt res;
  	res.v=min(Lp.v,Rp.v),res.l=Lp.l,res.r=Rp.r;
    //v 是当前区间的答案，l,r 是当前区间的左右界
  	int L=Lp.r,R=Rp.l,tmp=inf,_L,_R;bool fl=1;
  	for(int i=30;i>=0;i--){
  	  res.pre[i]=Lp.pre[i]?Lp.pre[i]:Rp.pre[i];//更新当前区间第 i 位的 P，不存在为 0
  	  res.suf[i]=Rp.suf[i]?Rp.suf[i]:Lp.suf[i];//更新当前区间第 i 位的 Q，不存在为 0
  	  if(!fl) continue;//高位无法满足条件直接跳过
  	  if(!Lp.suf[i]&&!Rp.pre[i]){fl=!lim[i];continue;}//这一位无法为 1 满足条件
  	  if(!lim[i]) _L=L,_R=R;
  	  if(!Lp.suf[i]) R=max(R,Rp.pre[i]);
  	  else if(!Rp.pre[i]) L=min(L,Lp.suf[i]);
  	  else{
  	  	if(S(Lp.suf[i],Lp.r)<=S(Rp.l,Rp.pre[i])) L=min(L,Lp.suf[i]);
  	  	else R=max(R,Rp.pre[i]);
  	  }
  	  if(!lim[i]) tmp=min(tmp,S(L,R)),L=_L,R=_R;//在不要求选 1 时选了 1，可以直接更新答案
  	}
  	if(fl) res.v=min(res.v,S(L,R));
  	res.v=min(res.v,tmp);
  	return res;
  }

完成了区间合并，那么这道题就做完了。其实只要想到拆位，也就不难了。

实现中 $a$ 的区间最大值可以用 ST 表维护做到 $O (1)$ ，那么总时间复杂度是 $O (q \log n \log V + n \log V)$ ，后者是预处理的复杂度。

const int N=2e5+5,inf=2e9;
int n,T,m,V,a[N],st[30][N],b[N],lg[N],lim[31];

void init(){
  lg[1]=0;
  for(int i=2;i<=n;i++) lg[i]=lg[i/2]+1;
  for(int i=1;i<=lg[n]+1;i++)
    for(int j=1;j+(1<<i)-1<=n;j++)
      st[i][j]=max(st[i-1][j],st[i-1][j+(1<<(i-1))]);
}

int S(int l,int r){
  int tmp=lg[r-l+1];
  return max(st[tmp][l],st[tmp][r-(1<<tmp)+1]);
}

namespace SGT{
  struct sgt{
    int v,pre[31],suf[31],l,r;
  }tr[N<<2];
  #define mid ((l+r)>>1)
  #define lc p<<1
  #define rc p<<1|1
  #define lson l,mid,lc
  #define rson mid+1,r,rc
  sgt operator +(sgt Lp,sgt Rp){
  	sgt res;
  	res.v=min(Lp.v,Rp.v),res.l=Lp.l,res.r=Rp.r;
  	int L=Lp.r,R=Rp.l,tmp=inf,_L,_R;bool fl=1;
  	for(int i=30;i>=0;i--){
  	  res.pre[i]=Lp.pre[i]?Lp.pre[i]:Rp.pre[i];
  	  res.suf[i]=Rp.suf[i]?Rp.suf[i]:Lp.suf[i];
  	  if(!fl) continue;
  	  if(!Lp.suf[i]&&!Rp.pre[i]){fl=!lim[i];continue;}
  	  if(!lim[i]) _L=L,_R=R;
  	  if(!Lp.suf[i]) R=max(R,Rp.pre[i]);
  	  else if(!Rp.pre[i]) L=min(L,Lp.suf[i]);
  	  else{
  	  	if(S(Lp.suf[i],Lp.r)<=S(Rp.l,Rp.pre[i])) L=min(L,Lp.suf[i]);
  	  	else R=max(R,Rp.pre[i]);
  	  }
  	  if(!lim[i]) tmp=min(tmp,S(L,R)),L=_L,R=_R;
  	}
  	if(fl) res.v=min(res.v,S(L,R));
  	res.v=min(res.v,tmp);
  	return res;
  }
  void pu(int p){tr[p]=tr[lc]+tr[rc];}
  void Up(int p,int l){
    tr[p].l=tr[p].r=l,tr[p].v=(b[l]>=V)?a[l]:inf;
    for(int i=0;i<31;i++) tr[p].pre[i]=tr[p].suf[i]=((b[l]>>i)&1)?l:0;
  }
  void build(int l,int r,int p){
    if(l==r) return Up(p,l);
    build(lson),build(rson),pu(p);
  }
  void upd(int l,int r,int p,int x){
  	if(l==r) return Up(p,l);
  	x<=mid?upd(lson,x):upd(rson,x);pu(p);
  }
  sgt qry(int l,int r,int p,int x,int y){
  	if(x<=l&&y>=r) return tr[p];
  	if(y<=mid) return qry(lson,x,y);
  	if(x>mid) return qry(rson,x,y);
  	return qry(lson,x,y)+qry(rson,x,y);
  }
}
using namespace SGT;

void sol(){
  cin>>n>>V;
  for(int i=0;i<31;i++) lim[i]=((V>>i)&1);
  for(int i=1;i<=n;i++) cin>>a[i],st[0][i]=a[i];
  for(int i=1;i<=n;i++) cin>>b[i];
  init();build(1,n,1);
  cin>>m;
  while(m--){
  	int op,l,r;cin>>op>>l>>r;
  	if(op==1) b[l]=r,upd(1,n,1,l);
  	else{
  	  sgt res=qry(1,n,1,l,r);
  	  if(res.v==inf) cout<<"-1 ";
  	  else cout<<res.v<<' ';
  	}
  }
  cout<<'\n';
}

int main(){
  ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  cin>>T;
  while(T--) sol();
  return 0;
}

Conclusion

有关二进制的 DS 可以考虑拆位，对每一位分别进行讨论。（F）
构造题可以考虑把每一个询问分开来考虑。（C）
图论边数过多时，我们可以考虑前缀和优化，也可以 对点按照权值排序，边权为 $0$ 的边是有传递性的。（E）

上一篇ARC172 - sol

下一篇1934.Codeforces Round 931 (Div. 2) - sol

本文作者：H_W_Y

本文链接：https://www.cnblogs.com/H-W-Y/p/18047267/cf1937

posted @ 2024-03-01 15:51 H_W_Y 阅读(134) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

H_W_Y

用拼搏，为自己注解；用努力，为成功奠基

1937.Codeforces Round 930 (Div. 2) - sol

A. Shuffle Party

B. Binary Path

C. Bitwise Operation Wizard

D. Pinball

E. Pokémon Arena

F. Bitwise Paradox

Conclusion

公告

常用链接

我的标签

合集

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论