20230703-动态规划DP 1
20230703
热身
题目
求长度为n的合法括号序列有多少个,对\(10^9+7\)取模。
\(n\)为偶数,\(n\le 10^6\)。
Solution
可以维护一个栈
遇到一个左括号就加入栈
而遇到右括号时就取栈顶的左括号与它配对出栈
一个合法序列需要保证:
- 最后栈为空,即所有的左括号都和有括号配对了
- 中间不能出现遇到一个右括号时栈里没有左括号了
这样我们可以把栈里的括号数量转化到平面直角坐标系上面
这样可以得到一条折线
而这条折线就对应一个括号序列
它是合法的当且仅当:
- 没有一部分跑到了x轴下方
- 最后折线结束在(n,0)的位置
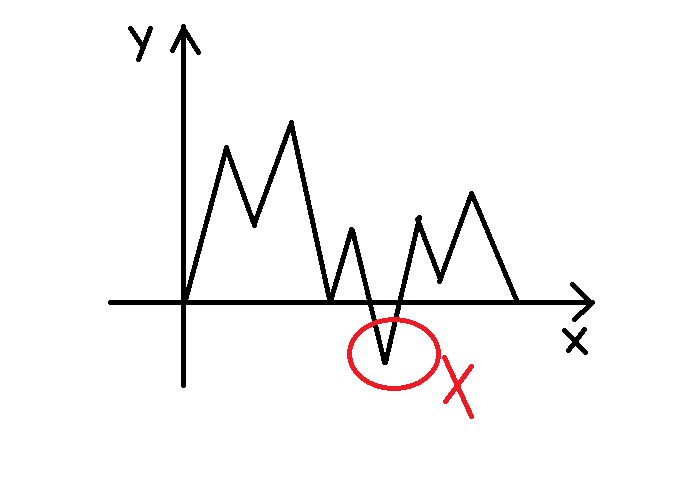
图中这个序列是不合法的,因为红色圈起来的地方在x轴下方了
我们考虑将这样的折线转化成横平竖直的变化
考虑再建立一个平面直角坐标系
把原来的也放进去
我们把x轴逆时针旋转45度
得到了一条直线\(l1:y=x\)
那么我们每一次的变化可以转化为从原点向前走和向上走
但是不能超过这条直线\(l1:y=x\)
最终走到\((n,n)\)
由于不超过很难去判断
我们可以在设一条直线\(l2:y=x+1\)
这样走的路径不碰到\(l2\)即可
而对于每一个碰到\(l2\)的折线
我们考虑把它沿着\(l2\)翻折
这样起点\((0,0)\)就变到了\((-1,1)\)
在\((0,0) \to (n,n)\)的方案中
有部分合法有部分不合法
而那部分不合法的我们把它翻折过去
成了\((-1,1) \to (n,n)\)的方案
这样方案数就是
\((0,0) \to (n,n)的方案数 - (-1,1) \to (n,n)的方案数\)
再来考虑怎么计算
从\((0,0) \to (n,n)\)我们一共会走\(2n\)步
而每一步我们可以选择向上和向右之间的一种
而一共需要\(n\)步向上和\(n\)步向右
方案数相当于在\(2n\)个东西中选\(n\)个向上走的方案数
也就是\(C_{2n}^{n}\)
同理
从\((-1,1) \to (n,n)\)的方案数就是
\(C_{2n}^{n-1}\)
这样答案就为\(C_{2n}^{n}-C_{2n}^{n-1}\)
这个数也就是卡特兰数
树形DP
CF581F Zublicanes and Mumocrates
题目大意
传送门
给出一棵n个点的树,保证它有偶数个叶子节点,请对该树的所有节点进行黑白染色,使得黑色与白色的叶子节点数相等,且直接连接两个异色点的边数最少。
\(n \le 5000\)
Solution
很明显的树形DP
考虑\(f[u][i][0/1]\)表示在节点\(u\)的子树中
叶子结点为黑色的有\(i\)个,当前节点颜色为黑色1白色0的最小边数
考虑依次枚举\(u\)的每一个儿子\(v\)
那么我们的\(f\)可以由上一个儿子更新的状态转移过来
那么
\(f[u][i+j][0]=f[u][i][0]+min(f[v][j][0],f[v][j][1]+1)\)
\(f[u][i+1][1]=f[u][i][1]+min(f[v][j][1],f[v][j][0]+1)\)
但是发现以前的\(f\)是很有可能被改变的
而组成\(k=i+j\)也有很多种情况
所以在每一次更新前
我们需要再用一个数组\(g[i][j]=f[u][i][j]\)来记录上一次的情况
同时将\(f[u][i][j]\)初始化为inf
在更新过程中每次取min即可
还要注意需要两次dfs
第一次来预处理,扫一遍数统计叶子结点的个数
而我们不能用叶子结点为根,所以根很有可能不是1
得知叶子结点个数就可以知道dp枚举的范围
第二次在进行数形DP即可
H_W_Y-Coding
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e4+10;
int n,head[maxn],tot=0,f[5005][5005][2],in[maxn],cnt=0,rt,siz[maxn],g[5005][2];
struct edge{
int v,nxt;
}e[maxn*2];
inline void add(int u,int v){
e[++tot]=(edge){v,head[u]};
head[u]=tot;
e[++tot]=(edge){u,head[v]};
head[v]=tot;
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)){x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
return x*f;
}
inline void dfs1(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;in[u]++;
if(v==fa) continue;
dfs1(v,u);
}
cnt+=(in[u]==1);
}
inline void dfs2(int u,int fa){
if(in[u]==1){
f[u][0][0]=f[u][1][1]=0;siz[u]=1;
return;
}
bool flag=false;siz[u]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].v;
if(v==fa) continue;
dfs2(v,u);
if(!flag){
for(int j=0;j<=siz[v];j++)
f[u][j][0]=min(f[v][j][0],f[v][j][1]+1),
f[u][j][1]=min(f[v][j][1],f[v][j][0]+1);
}
else{
for(int j=0;j<=min(siz[u],cnt/2);j++)
for(int k=0;k<2;k++)
g[j][k]=f[u][j][k],f[u][j][k]=0x3f3f3f3f;//初始化,后面dp的时候f会改变
for(int j=0;j<=min(siz[v],cnt/2);j++)
for(int k=0;k<=min(siz[u],cnt/2-j);k++)
f[u][j+k][0]=min(f[u][j+k][0],g[k][0]+min(f[v][j][0],f[v][j][1]+1)),
f[u][j+k][1]=min(f[u][j+k][1],g[k][1]+min(f[v][j][1],f[v][j][0]+1));
}
flag=true;siz[u]+=siz[v];
}
}
int main(){
/*2023.7.4 H_W_Y CF581F Zublicanes and Mumocrates 树形DP*/
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v);
}
dfs1(1,0);rt=1;
while(in[rt]==1) rt++;
memset(f,0x3f,sizeof(f));
dfs2(rt,0);
printf("%d\n",min(f[rt][cnt/2][0],f[rt][cnt/2][1]));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号