hihocoder 第四十周 三分求极值

　　题目链接：http://hihocoder.com/contest/hiho40/problem/1 ,一道简单的三分。

 

---

 

　　题目是在直角坐标系中有一条抛物线y=ax^2+bx+c和一个点P(x,y)，求点P到抛物线的最短距离d。

用提示的算法：

　　当函数是凸形函数时，二分法无法适用，这时就需要用到三分法。

　　从三分法的名字中我们可以猜到，三分法是对于需要逼近的区间做三等分：

　　

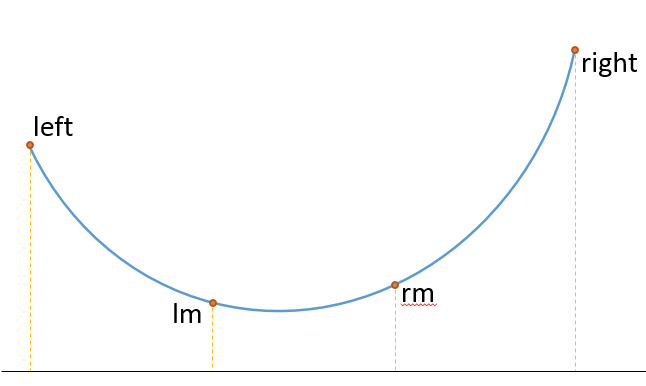
　　我们发现lm这个点比rm要低，那么我们要找的最小点一定在[left,rm]之间。如果最低点在[rm,right]之间，就会出现在rm左右都有比他低的点，这显然是不可能的。 同理，当rm比lm低时，最低点一定在[lm,right]的区间内。利用这个性质，我们就可以在缩小区间的同时向目标点逼近，从而得到极值。

 

#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <stack>
#include <cmath>
#include <string>
#include <string.h>
#include <algorithm>
using namespace std;
#define eps 1e-8
double a , b , c , X , Y;
inline double f(double x)
{
    return (X - x) * (X - x) + 
        (a * x * x + b * x + c - Y) * (a * x * x + b * x + c - Y);
}
double ternary_search(double l , double r)
{
    double lm = (2 * l + r) / 3;
    double rm = (l + 2 * r) / 3;
    while(r - l >= eps) {
        if(f(lm) < f(rm))
            r = rm;
        else
            l = lm;
        lm = (2 * l + r) / 3;
        rm = (l + 2 * r) / 3;
    }
    return lm;
}
int main()
{
    scanf("%lf %lf %lf %lf %lf" , &a , &b , &c , &X , &Y);
    if(f(X) <= eps) {
        printf("0.000\n");
    } else {
        double x = ternary_search(-500 , 500);
        printf("%.3lf\n" , sqrt(f(x)));
    }
    return 0;
}