树状数组和线段树
树状数组
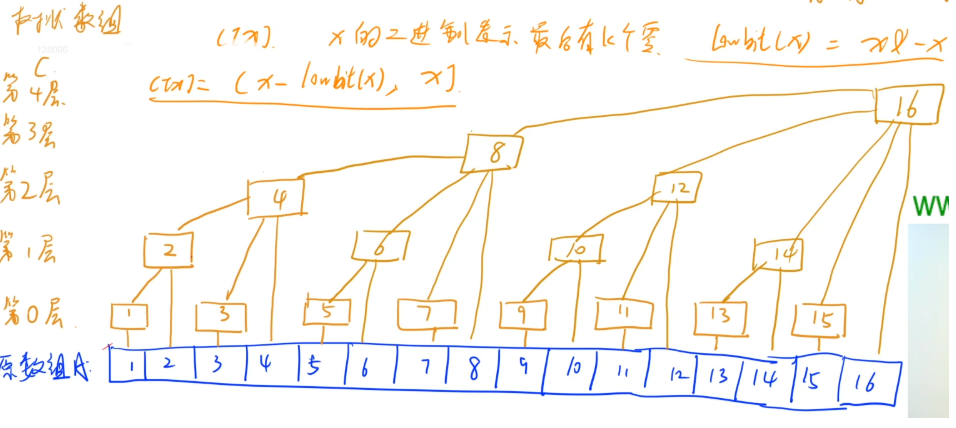
数组的奇数为存放数组原来的值，偶数位数组的第x个位置表示的是(x - lowbit(x), x]这个区间内元素的和
lowbit()函数表示包括当x在内的lowbit(x)个元素的和在x的位置上已知
| 4层 | 16（16） | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3层 | 8（8） | |||||||||||||||
| 2层 | 4（4） | 12（4） | ||||||||||||||
| 1层 | 2（2） | 6（2） | 10（2） | 14（2） | ||||||||||||
| 0层 | 1 | 3 | 5 | 1 | 9 | 11 | 13 | 15 | ||||||||
| 原数组 | 1 | 2(0010) | 3 | 4(0100) | 5 | 6(0110) | 7 | 8(1000) | 9 | 10 (1010) | 11 | 12 (1100) | 13 | 14 (1110) | 15 | 16 (10000) |
由上表可以找出规律：
lowbit(x)的值为2^k(k为第i个数转换成二进制后有几位0的个数)，可以用位运算 x & -x 得到结果
例：给定 n 个数组成的一个数列，规定有两种操作，一是修改某个元素，二是求子数列 [a,b]的连续和。
输入格式
第一行包含两个整数 n 和 m，分别表示数的个数和操作次数。第二行包含 n 个整数，表示完整数列。接下来 m 行，每行包含三个整数 k,a,b （k=0，表示求子数列[a,b]的和；k=1，表示第 a 个数加 b）。数列从 1 开始计数。
输出格式
输出若干行数字，表示 k=0时，对应的子数列 [a,b] 的连续和。
数据范围
1≤n≤1000001≤n≤100000,1≤m≤1000001≤m≤100000，1≤a≤b≤n1≤a≤b≤n,数据保证在任何时候，数列中所有元素之和均在 int 范围内。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100010;
int m, n;
int a[N], tr[N];
//lowbit(x)函数用来判断x的二进制后有k位0，返回2^k，k为x所在的层数
int lowbit(int x){
return x & (-x); //负数用补码表示：按位取反再加一；正数用原码表示，且都没有符号位
}
void add(int x, int v){
for(int i = x; i > 0; x -= lowbit(i))tr[i] += v;//不光要在x位置上+v，在其子树上也要+v
}
int query(int x){
int res = 0;
for(int i = x; i > 0; i -= lowbit(i)) res += tr[i];
return res;
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
for(int i = 1; i <= n; i++) add(i, a[i]);
while(m--){
int k, x, y;
scanf("%d%d%d", &k, &x, &y);
if(k == 0){
printf("%d\n", query(y) - query(x - 1));
}else{
add(x, y);
}
}
return 0;
}
总结：本题和原来的前缀和区别：
| 原方法 | 树状数组 | |
|---|---|---|
| 求前缀和（查找） | O(1) | O(logn) |
| 动态加 | O(n) | O(logn) |
| 平均 | O(n) | O(logn) |
线段树(二叉树)
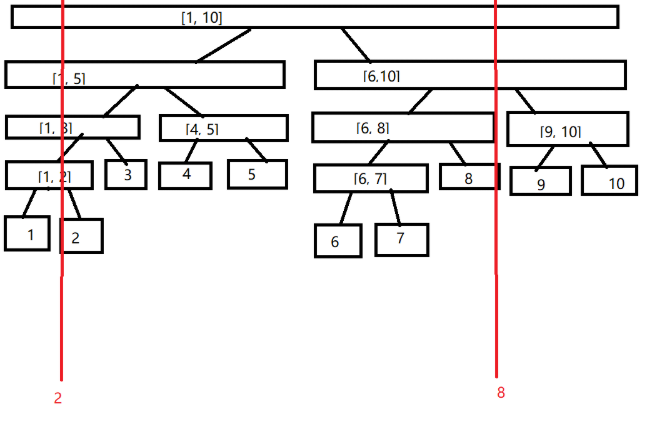
线段树用数组存储x的父节点为x/2(x>>1), 左儿子为2x(x<<1), 右儿子为2x+1(x<<1 | 1)、并且线段树求和的操作也可以替换为其他操作，如求区间中最大最小值
#include<iostream>
#include<cstring>
#include<algorithm>
#incldue<cstdio>
using namespace std;
const int N = 100010
int m, n;
int w[N];
typedef struct Node{
int l, r;
int sum;
}tr[N * 4];
void pushup(int u){
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
void build(int u, int l, int r){
if(l == r) tr[u] = {l, r, w[r]} //如果是叶节点sum就是自己，C语言中可以以表的形式给结点顺序赋值
else{
int mid = l + r >>1;
build(u << 1, l, mid); //左儿子
build(u << 1 | 1, mid + 1, r); //右儿子
pushup(u); //将左二子和右儿子的值求和
}
}
int query(int u, int l, int r){
if(tr[u].l >= l && tr[u].r <= r) return tr[u].sum;
int mid = tr[u].l + tr[u].r >> 1; //以小区间的中点为判断依据
int sum = 0;
if(l <= mid) sum += query(u << 1, l, r); //看当前区间是否落在求和区间中，如果在遍历它的左子树
if(r >= mid + 1) sum += query(u << 1 | 1, l, r); //如果在遍历它的右子树
return sum;
}
void modify(int u, int x, int v){
if(tr[i].l == tr[i].r) tr[i].sum += v;
else{
int mid = tr[i].l + tr[i].r >> 1;
if(x <= mid)modify(x << 1, x, v);
else modify(x << 1 | 1, x, v);
pushup(u);
}
}
int main(){
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)scanf("%d", &w[i]);
build(1, 1, n);
int k, a, b;
while(m--){
scanf("%d%d%d", &k, &a, &b);
if(k == 0) printf("%d\n", query(1, a, b))
else modify(1, a, b);
}
}
复杂度：
单点修改O(logn)
区间查询O(logn)
