AGC029记录
希望能快点把状态找回来......

A:逆序对
由于只有两种字符,逆序对可以 \(O(n)\) 实现。
B:贪心
可以注意到如果从大往小匹配,一个数只可能会和比它小的数匹配上。
于是,从大到小枚举,每次贪心地能匹配就匹配,这个过成可以用 map 轻松实现。
记得特判能和自己匹配的。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il int read(char *s){
int len=0;
register char ch=getchar();
while(ch==' '||ch=='\n') ch=getchar();
while(ch!=' '&&ch!='\n'&&ch!=EOF) s[++len]=ch,ch=getchar();
return len;
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=2e5+7;
ll n;
map<ll,ll> f;
ll base[64],ans,a[MAXN];
#define IT map<ll,ll>::iterator
il ll count(ll x){
int cnt=0;
for(;x;x>>=1) cnt+=x&1;
return cnt;
}
int main(){
n=read();
for(ri i=1;i<=n;++i)a[i]=read();
base[0]=1;
for(ri i=1;i<=62;++i) base[i]=base[i-1]<<1;
sort(a+1,a+n+1);
for(ri i=1;i<=n;++i) f[a[i]]++;
int j=60;
for(IT it=--f.end();;--it){
while(base[j-1]>=it->first) --j;
if(count(it->first)==1){
ans+=it->second/2;
it->second&=1;
}
if(f.find(base[j]-it->first)!=f.end()){
ll res=min(it->second,f[base[j]-it->first]);
it->second-=res,f[base[j]-it->first]-=res;
ans+=res;
}
if(it==f.begin()) break;
}
print(ans);
return 0;
}
C:二分+贪心
显然可以二分答案,难点在于如何去check当前的方案是否合法。
不难发现,存在一个贪心策略,每次都让当前的字典序尽量小。
进行分讨:
- \(a_{i}<a_{i+1}\)
直接在 \(s_{i}\) 的基础上一直添加0。 - \(a_{i}>a_{i+1}\)
那么把 \(s_{i}\) 中超过 \(a_{i+1}\) 的部分全部删去,再将 \(s_{i}\) 中第 \(a_{i+1}\) 的位置++ ,要记得进位。
这个过程可以用一个栈模拟,当最后在 \(1\) 的位置进位了,则不合法,否则合法。
倘若直接这样暴力模拟,复杂度是 \(O(\sum^{}_{}a_{i})\) 的,考虑优化。
不难发现,中间的一大串 0 是没有用的,可以直接跳过这一部分,直接记录当前的 \(s_{i}\) 中不为 0 的位置。
大概可以用势能分析得到这个过程是 \(O(n)\) 的,因此总时间复杂度为 \(O(n \log n)\)。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
const int MAXN=2e5+7;
ll n,a[MAXN];
/*
贪心地构造,肯定是每次尽量让当前的字典序小
二分答案这个不用质疑
*/
int top;
#define pii pair<int,int>
pii sta[MAXN];
int insert(int pos,int x){
if(!pos) return 0;
while(top&&sta[top].first>pos) --top;
if(sta[top].first==pos){
sta[top].second++;
}
else sta[++top]=(pii){pos,1};
if(sta[top].second==x){
top--;
return insert(pos-1,x);
}
return 1;
}
int check(int x){
top=0;
for(ri i=2;i<=n;++i){
if(a[i]>a[i-1]) continue;
if(!insert(a[i],x)) return 0;
}
return 1;
}
int main(){
n=read();
for(ri i=1;i<=n;++i) a[i]=read();
int l=1,r=n,ans,mid;
while(l<=r){
mid=(l+r)>>1;
if(check(mid)){
ans=mid;
r=mid-1;
}
else l=mid+1;
}
print(ans);
return 0;
}
D:贪心
非常一眼的题目。
首先可以发现,每一回合高木都会向右移动一个单位,否则的话青木可以选择不动,游戏结束。
也就是说,高木的行动是确定的,剩下的只剩下青木了。
于是,有一个比较naive的贪心,即先将所有障碍物按照 \(x\) 排序,再依次扫过去。
假设当前枚举道的障碍物是 \((x,y)\) ,那么如果青木可以到达 \((x-1,y)\) ,则答案就是 \(x-1\) 。
考虑如何判断青木在 \(x-1\) 的时候纵坐标可以到达 \(y\) 。
不难发现,在 \(x\) 固定的时候且没有碰到障碍物的时候,青木能到达的范围都是一个区间 \([1,up]\),每次 \(x+1\) 都会让 \(up++\) 。
当出现障碍物的时候,设其坐标为 \((x+1,lim)\) ,需要分三类讨论:
- \(lim>up+1\)
这个障碍物对 \(up\) 没有影响。 - \(lim=up+1\)
\(up\) 不能加一了。 - \(lim \leq up\)
此时已经得到答案为 \(x\),可以直接break。
至此,该如何得到答案已经非常简单了,这里就不再赘述了。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
/*
可以发现每次能到达的地方都是一段区间。
*/
#define pii pair<int,int>
set<pii > s;
int up;
const int MAXN=2e5+7;
pii p[MAXN];
int h,w,n;
int main(){
h=read(),w=read(),n=read();
for(ri i=1;i<=n;++i) p[i].first=read(),p[i].second=read();
p[++n]=(pii){h+1,1};
sort(p+1,p+n+1);
up=1;
for(ri i=1,j=1;i<=n;++i){
while(j+1<p[i].first){
++j;
if(s.find((pii){j,up+1})==s.end()) ++up;
}
if(up>=p[i].second&&s.find((pii){j,up})==s.end()){
print(j);
return 0;
}
s.insert(p[i]);
}
return 0;
}
E:树型dp
STO x义x
首先有个一眼的 \(O(n^2 \log n)\) 的暴力,就是直接照着题目要求模拟。
同时,还能发现如果以 1 为根,儿子 \(u\) 和它的父亲 \(v\) 在计算的过程中除了 \(u\) 的子树中这一段以外其它部分都是一样的。
这是树型dp的特点。
接下来考虑怎么从父亲那里继承答案。
令 \(mx_{u}\) 表示从 \(fa_{u} \longrightarrow 1\) 这一条路径上的最大值(这里从 \(fa_{u}\) 开始是为了方便后面的式子)。
那么以 \(u\) 为出发点的时候 \(u\) 内部子树的选取应该是所有到 \(u\) 的路径上都没有出现过比 \(mx_{u}\) 大的点。
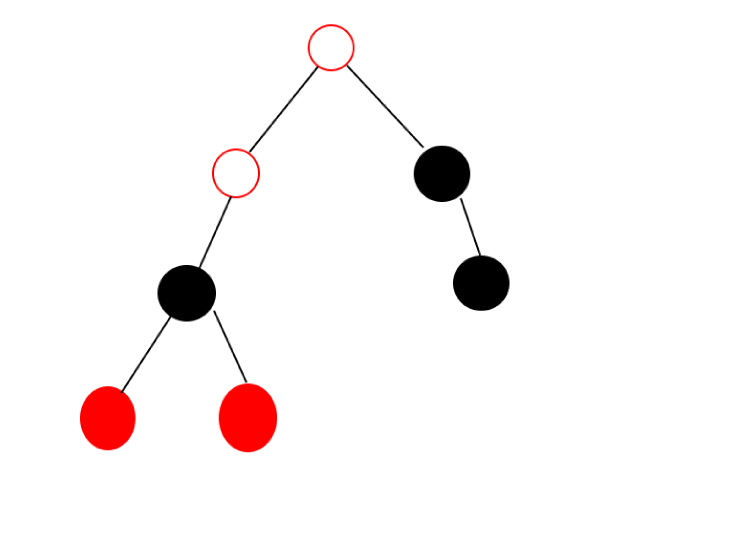
以这张图为例,红色的表示比 \(mx_u\) 小的,黑色的表示比 \(mx_u\) 大的,实心表示未选取的,空心表示选取的。
设 \(p_{u,w}\) 表示以 \(u\) 为根的子树中从 \(u\) 出发,按照上述操作且不超过 \(w\) 的选取点的个数(即使起点 \(u\) 比 \(w\) 大也会强制选择)。
设 \(f_{u}\)表示从 \(u\) 出发的最后答案。
需要进行一个分讨:
-
\(u>mx{fa}\)
那么在 \(fa\) 操作的时候是不会拓展到 \(u\) 的子树中的,所以把 \(u\) 的子树贡献算上就行了。
\(f_{u}=f_{fa}+p_{u,mx_{u}}\) -
\(u<mx{fa}\)
树型dp的容斥套路,可以发现 \(f_{fa}\) 与 \(p_{u,mx_{u}}\) 的公共部分是 \(p_{u,mx_{fa}}\) ,直接把这部分多算的减掉。
\(f_{u}=f_{fa}+p_{u,mx_{u}}-p_{u,mx_{fa}}\)
而得到 \(p_{u,w}\) 的过程可以直接记忆化搜索,大概口胡一下为什么这样子复杂度是对的。
- \(mx_{u}>mx_{fa}\)
那么在计算 \(p_{fa_{fa},mx_{fa_{fa}}}\) 的时候是不会搜到子树 \(u\) 内来的。 - \(mx_{u}=mx_{fa}\)
那么在计算 \(p_{fa,mx_{fa}}\) 的时候已经顺带着计算过了 \(p_{u,mx_{u}}\) 了。
因此,每个点所存的状态无非就只有 \(p_{u,mx_{u}}\) 和 \(p_{u,mx_{fa}}\) 这样两种。
所以总时间复杂度 \(O(n\log n)\) ,空间复杂度 \(O(n)\),瓶颈在于map(当然可以写一个双关键字哈希表做到期望 \(O(n)\)) 。
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar(' ');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
int n;
const int MAXN=2e5+7;
vector<int> g[MAXN];
map<int,int> p[MAXN];
int fa[MAXN],mx[MAXN];
int solve(int u,int w){
if(p[u].find(w)!=p[u].end()) return p[u][w];
int res=1;
for(ri i=0;i<g[u].size();++i){
int v=g[u][i];
if(v==fa[u]||v>w) continue;
res+=solve(v,w);
}
return p[u][w]=res;
}
void dfs(int u,int f){
fa[u]=f;
mx[u]=max(mx[f],f);
for(ri i=0;i<g[u].size();++i){
int v=g[u][i];
if(v==f) continue;
dfs(v,u);
}
}
int f[MAXN];
/*
*/
void dfs1(int u,int fa){
if(fa){
if(u>mx[fa]) f[u]=f[fa]+solve(u,mx[u]);
else f[u]=f[fa]+solve(u,mx[u])-solve(u,mx[fa]);
}
else f[u]=0;
for(ri i=0;i<g[u].size();++i){
int v=g[u][i];
if(v==fa) continue;
dfs1(v,u);
}
}
int main(){
n=read();
for(ri i=1;i<n;++i){
int u=read(),v=read();
g[u].push_back(v);
g[v].push_back(u);
}
dfs(1,0);
dfs1(1,0);
for(ri i=2;i<=n;++i) print(f[i]);
return 0;
}
F:二分图+构造
神仙题+1。
虽然是一颗无根树,但是可以发现对于任意一颗无根树,都可以去随便钦定一个根,最后的结果是一样的。
这么做还能顺便把边给定向了。
而对于有根树来说,其必要条件是除了根以外每个点的入度都为1。
先不考虑每个点的父亲是谁,只考虑每个点是否可能有通向父亲的边。
那么可以让集合向其内部的点连边,跑二分图匹配,用Dinic实现的话是 \(O(m \sqrt(n) )\) 的。
如果最后匹配数量不为 \(n-1\) ,显然无解,否则令没有被匹配上的那个点作为 \(root\)。
接下来考虑如何去构造出合法方案。
目前已知的是每条边的终点,需要给每条边定一个起点,同时还知道每条边起点的可能点的点集。
这样又是一个匹配过程。
构造方案是从 \(root\) 出发开始 dfs ,把从当前点 \(u\) 能到达的所有还未找到父亲的点 \(v\) 都匹配起来,令 \(v\) 的父亲为 \(u\) 。
首先这种匹配方式的正确性显然,每次 dfs 都是往外扩展出一条链。
充分性不会证,测了一下发现把边 random_shuffle 了之后还是能过,就当作它是充分的了吧
Code
#include<bits/stdc++.h>
using namespace std;
#define il inline
#define ri register int
#define ll long long
#define ui unsigned int
il ll read(){
bool f=true;ll x=0;
register char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=false;ch=getchar();}
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
if(f) return x;
return ~(--x);
}
il void write(const ll &x){if(x>9) write(x/10);putchar(x%10+'0');}
il void print(const ll &x) {x<0?putchar('-'),write(~(x-1)):write(x);putchar('\n');}
il ll max(const ll &a,const ll &b){return a>b?a:b;}
il ll min(const ll &a,const ll &b){return a<b?a:b;}
int cnt=-1,n,s,t;
const int MAXN=1e6+7;
const int N=4e5+7;
int dep[N],rad[N];
struct edge
{
int to;
ll w;
bool operator<(const edge &x)const{
return w<x.w;
}
}e[MAXN];
vector<int> g[N];
void add(int U,int V,ll W){
e[++cnt]=(edge){V,W};
g[U].push_back(cnt);
e[++cnt]=(edge){U,0};
g[V].push_back(cnt);
}
bool bfs(){
memset(dep,0,sizeof(dep));
memset(rad,0,sizeof(rad));
queue<int> q;
dep[s]=1;
q.push(s);
while(!q.empty()){
int S=q.front();q.pop();
for(ri i=rad[S];i<g[S].size();++i){
edge now=e[g[S][i]];
if(!now.w||dep[now.to]) continue;
dep[now.to]=dep[S]+1;
q.push(now.to);
}
}
return dep[t];
}
ll FF(int u,ll flow){
if(u==t) return flow;
ll out=0;
for(ri i=rad[u];i<g[u].size();++i){
rad[u]=i;
edge &now=e[g[u][i]];
int v=now.to;
if((!now.w)||(dep[v]!=dep[u]+1)) continue;
ll res=FF(v,min(flow,now.w));
now.w-=res;
e[g[u][i]^1].w+=res;
flow-=res;
out+=res;
if(!flow) break;
}
if(!out) dep[u]=0;
return out;
}
ll ans;
int root;
int from[MAXN],mark[MAXN],tot;
int lstans[MAXN][2];
void dfs(int u){
if(mark[u]) return;
for(ri i=0;i<g[u].size();++i){
int v=e[g[u][i]].to;
if(mark[v]||v==t) continue;
lstans[v][0]=u-n,lstans[v][1]=from[v]-n;
mark[v]=1,++tot;
dfs(from[v]);
}
}
int main(){
// freopen("in04.txt","r",stdin);
// freopen("1.out","w",stdout);
n=read();
s=0,t=2*n+1;
for(ri i=1;i<=n;++i) add(n+i,t,1);
for(ri i=1;i<n;++i) {
add(s,i,1);
int m=read();
for(ri j=1;j<=m;++j){
int u=read();
add(i,n+u,1);
}
}
while(bfs()) ans+=FF(s,1e9);
if(ans!=n-1) return !puts("-1");
for(ri i=1;i<=n;++i){
int u=n+i;
for(ri j=0;j<g[u].size();++j){
if(e[g[u][j]].to!=t){
if(e[g[u][j]].w) from[e[g[u][j]].to]=u;
}
else if(e[g[u][j]].w){
root=u;
}
}
}
for(ri i=1;i<=2*n;++i) random_shuffle(g[i].begin(),g[i].end());
mark[s]=mark[t]=1;
dfs(root);
if(tot==n-1){
for(ri i=1;i<n;++i) printf("%d %d\n",lstans[i][0],lstans[i][1]);
}
else puts("-1");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号