top 100 liked Q (26-)

26. 合并区间（56）

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:

输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

解题思路：

27. 不同路径（62）

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

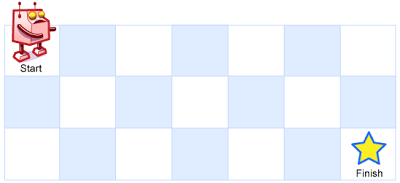
例如，上图是一个7 x 3 的网格。有多少可能的路径？

说明：m 和 n 的值均不超过 100。

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:

输入: m = 7, n = 3
输出: 28

解题思路：　　

动态规划：第一行与第一列都初始化为1，因为到达这些方格的方法只有一种。

其他方格：dp[i][j]=dp[i-1][j]+dp[i][j-1];

 1 class Solution {
 2 public:
 3     int uniquePaths(int m, int n) {
 4         
 5         if(m<2 || n<2)
 6             return 1;
 7         
 8         vector<vector<int>> dp(m,vector<int>(n,1));
 9         for(int i=1;i<m;i++)
10             for(int j=1;j<n;j++)
11                 dp[i][j]=dp[i-1][j]+dp[i][j-1];
12         
13         return dp[m-1][n-1];
14     }
15 };

View Code

28. 最小路径和(64)

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

解题思路：　　

动态规划：第一行第一列对前面的元素累加

其他方格：dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j]

 1 class Solution {
 2 public:
 3     int minPathSum(vector<vector<int>>& grid) {
 4         int szx = grid.size();
 5         if(szx<1)
 6             return 0;
 7         int szy = grid[0].size();
 8         int dp[szx][szy];
 9         
10         dp[0][0]=grid[0][0];
11         for(int i=1;i<szx;i++){
12             dp[i][0]= grid[i][0] + dp[i-1][0];
13         }
14         
15         for(int i=1;i<szy;i++){
16             dp[0][i]= grid[0][i] + dp[0][i-1];       
17         }
18         
19          for(int i=1;i<szx;i++)
20              for(int j=1;j<szy;j++)
21                  dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
22         
23         return dp[szx-1][szy-1];
24     }
25 };

View Code

29. 爬楼梯(70)

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

解题思路：　　

动态规划：f(n) = f(n-1) + f(n-2)

初始值：f1=1, f2=2

 1 //f(n) = f(n-1) + f(n-2)
 2 
 3 class Solution {
 4 public:
 5     int climbStairs(int n) {
 6         if(n<3)
 7             return n;
 8         int first = 1, second =2;
 9         int res; 
10         for(int i=3;i<=n;i++){
11             res = first + second;
12             first = second;
13             second = res;
14         }
15         
16         return res;
17     }
18 };

View Code

30. 编辑距离(72)

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1:

输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:

输入: word1 = "intention", word2 = "execution"
输出: 5
解释: 
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

解题思路：　　

31. 颜色分类(75)

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意:
不能使用代码库中的排序函数来解决这道题。

示例:

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]

进阶：

一个直观的解决方案是使用计数排序的两趟扫描算法。
首先，迭代计算出0、1 和 2 元素的个数，然后按照0、1、2的排序，重写当前数组。
你能想出一个仅使用常数空间的一趟扫描算法吗？

解题思路：

32. 最小覆盖子串(76)

给定一个字符串 S 和一个字符串 T，请在 S 中找出包含 T 所有字母的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

说明：

如果 S 中不存这样的子串，则返回空字符串 ""。
如果 S 中存在这样的子串，我们保证它是唯一的答案。

解题思路：　　

33. 子集(78)

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: nums = [1,2,3]
输出:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

解题思路：　　

34. 单词搜索(79)

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

解题思路：　　

35. 柱状图中最大的矩形(84)

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

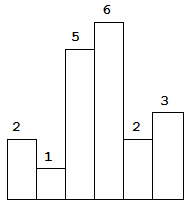
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

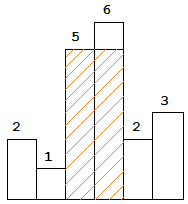
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10

解题思路：　　

36. 最大矩形(85)

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出: 6

解题思路：　　

37. 二叉树的中序遍历(94)🤣

给定一个二叉树，返回它的中序遍历。

示例:

输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]

解题思路-1：递归　　

注意遍历时节点值的添加位置！！

 1 /**
 2  * Definition for a binary tree node.
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 8  * };
 9  */
10 class Solution {
11 public:
12     vector<int> inorderTraversal(TreeNode* root) {
13         vector<int> res;
14         if(root==nullptr)
15             return res;
16         inorderTraversalCore(root, res);
17         return res;
18         
19     }
20     
21     //不要有返回值，不好处理
22     void inorderTraversalCore(TreeNode* root, vector<int>& res) {
23         if(root->left==nullptr && root->right==nullptr){
24             res.push_back(root->val);
25             return;
26         }
27             
28         if(root->left!=nullptr)
29             //不用在此处push_back,到叶结点的时候，左右子树为空，按照中间节点去添加元素（即下下行代码）
30             inorderTraversalCore(root->left,res); 
31         
32         res.push_back(root->val);
33         
34         if(root->right!=nullptr)
35             inorderTraversalCore(root->right,res);
36         
37         return;
38         
39     }
40 };

View Code

解题思路-2：迭代

38. 不同的二叉搜索树（96）

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

解题思路：　　

39. 验证二叉搜索树（98）

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1:

输入:
    2
   / \
  1   3
输出: true
示例 2:

输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

解题思路：　　

40. 对称二叉树（101）

给定一个二叉树，检查它是否是镜像对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

说明:

如果你可以运用递归和迭代两种方法解决这个问题，会很加分。

解题思路：　　

41. 二叉树的层次遍历（102）

给定一个二叉树，返回其按层次遍历的节点值。（即逐层地，从左到右访问所有节点）。

例如:
给定二叉树: [3,9,20,null,null,15,7],

返回其层次遍历结果：　　

[
  [3],
  [9,20],
  [15,7]
]

解题思路：　　

42. 二叉树的最大深度（104）

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。

解题思路：　　

左右子树深度的最大值+1

 1 /**
 2  * Definition for a binary tree node.
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 8  * };
 9  */
10 class Solution {
11 public:
12     int maxDepth(TreeNode* root) {
13         if(root==nullptr)
14             return 0;
15         int left = maxDepth( root->left)+1;
16         int right = maxDepth( root->right)+1;
17         return max(left,right);
18     }
19 };

View Code

43. 从前序与中序遍历序列构造二叉树（105）

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:
你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：　　

解题思路：　　

44. 二叉树展开为链表（114）

给定一个二叉树，原地将它展开为链表。

例如，给定二叉树

将其展开为：　　

解题思路：　　

45. 买卖股票的最佳时机（121）

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。

注意你不能在买入股票前卖出股票。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解题思路：　　

46. 二叉树中的最大路径和（124）

给定一个非空二叉树，返回其最大路径和。

本题中，路径被定义为一条从树中任意节点出发，达到任意节点的序列。该路径至少包含一个节点，且不一定经过根节点。

示例 1:

输入: [1,2,3]

       1
      / \
     2   3

输出: 6
示例 2:

输入: [-10,9,20,null,null,15,7]

   -10
   / \
  9  20
    /  \
   15   7

输出: 42

解题思路：　　

47. 最长连续序列（128）

给定一个未排序的整数数组，找出最长连续序列的长度。

要求算法的时间复杂度为 O(n)。

示例:

输入: [100, 4, 200, 1, 3, 2]
输出: 4
解释: 最长连续序列是 [1, 2, 3, 4]。它的长度为 4。

解题思路：　　

48. 只出现一次的数字（136）

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

输入: [2,2,1]
输出: 1
示例 2:

输入: [4,1,2,1,2]
输出: 4

解题思路：

使用异或即可

 1 class Solution {
 2 public:
 3     int singleNumber(vector<int>& nums) {
 4         int res = 0;
 5         int sz = nums.size();
 6         for(int i=0;i<sz;i++)
 7             res ^=nums[i];
 8         return res;
 9     }
10 };

View Code

49. 单词拆分（139）

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2：

输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。
示例 3：

输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false

解题思路：　　

50. 环形链表（141）

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

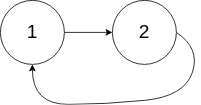
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

解题思路：　　

posted @ 2019-07-23 22:59 GuoXinxin 阅读(245) 评论(0) 编辑收藏举报

刷新页面返回顶部

GuoXinxin

top 100 liked Q (26-)

26. 合并区间（56）

27. 不同路径（62）

28. 最小路径和(64)

29. 爬楼梯(70)

30. 编辑距离(72)

31. 颜色分类(75)

32. 最小覆盖子串(76)

33. 子集(78)

34. 单词搜索(79)

35. 柱状图中最大的矩形(84)

36. 最大矩形(85)

37. 二叉树的中序遍历(94)🤣

38. 不同的二叉搜索树（96）

39. 验证二叉搜索树（98）

40. 对称二叉树（101）

41. 二叉树的层次遍历（102）

42. 二叉树的最大深度（104）

43. 从前序与中序遍历序列构造二叉树（105）

44. 二叉树展开为链表（114）

45. 买卖股票的最佳时机（121）

46. 二叉树中的最大路径和（124）

47. 最长连续序列（128）

48. 只出现一次的数字（136）

49. 单词拆分（139）

50. 环形链表（141）

公告