top 100 liked Q (1-25)
1. 两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
给定 nums = [2, 7, 11, 15], target = 9 因为 nums[0] + nums[1] = 2 + 7 = 9 所以返回 [0, 1]
解题思路-1:
存入map中,查找差值是否也在数组中,是则返回。
注意:一个元素只能用一次,数组可以有重复元素。

1 class Solution { 2 public: 3 vector<int> twoSum(vector<int>& nums, int target) { 4 int sz = nums.size(); 5 vector<int> res; 6 if(sz<2) 7 return res; 8 9 map<int,int> m; 10 for(int i=0;i<sz;i++){ 11 m[nums[i]]=i; 12 } 13 14 for(int i=0;i<sz-1;i++){ 15 if(m.find(target-nums[i]) != m.end() && m[target-nums[i]]!=i){ 16 res.push_back(i); 17 res.push_back(m[target-nums[i]]); 18 break; //不要忘记加break,否则会重复计算。 19 } 20 } 21 return res; 22 } 23 }; 24 /* 25 遇到的错误: 26 没有break:如果返回元素是索引 1与4,在1处添加1与4;在4处还会重复添加4与1。 27 if的判断条件有&& 28 后一个判断条件是索引不相等,而不是值不相等。因为数组中可能出现相同的元素。如[3,3] 29 */
解题思路-2:
使用一个HashMap(即 unordered_map)

1 class Solution { 2 public: 3 vector<int> twoSum(vector<int>& nums, int target) { 4 unordered_map<int, int> m; 5 vector<int> res; 6 for (int i = 0; i < nums.size(); ++i) { 7 m[nums[i]] = i; 8 } 9 for (int i = 0; i < nums.size(); ++i) { 10 int t = target - nums[i]; 11 if (m.count(t) && m[t] != i) { 12 res.push_back(i); 13 res.push_back(m[t]); 14 break; 15 } 16 } 17 return res; 18 } 19 };
简洁版(推荐,一次for循环即可)

1 class Solution { 2 public: 3 vector<int> twoSum(vector<int>& nums, int target) { 4 unordered_map<int, int> m; 5 for (int i = 0; i < nums.size(); ++i) { 6 if (m.count(target - nums[i])) { //当前i还没有被存入,找到的是之前存入的,因此不会出现找到的两个数是同一个元素的情况 7 return {i, m[target - nums[i]]}; 8 } 9 m[nums[i]] = i; 10 } 11 return {}; 12 } 13 };
2. 两数相加
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4) 输出:7 -> 0 -> 8 原因:342 + 465 = 807
解题思路:
从两个链表的头部开始计算,如果两个链表的值以及进位相加>=10,则继续进位(设置标志flag表示是否需要进位)
注意:
1)当两个链表共有长度处理完,还要处理较长的链表的剩余部分,并不是简单链接,还要考虑是否有共同相加时的进位。
2)当长的链表处理完,要考虑最高位(即最后一位是否有进位),如果有进位,添加一个新节点。

1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 class Solution { 10 public: 11 ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) { 12 if(l1==nullptr && l2==nullptr ) 13 return nullptr; 14 ListNode* res=new ListNode(0); 15 ListNode* p1=l1; 16 ListNode* p2=l2; 17 ListNode* phead = res; 18 int flag = 0,temp=0; 19 while(p1!=nullptr && p2!=nullptr){ //处理两个链表的公共部分 20 temp = p1->val + p2->val + flag; 21 if(temp>=10){ 22 flag =1; 23 temp = temp%10; 24 }else{ 25 flag = 0; 26 } 27 ListNode* tp = new ListNode(temp); 28 phead->next = tp; 29 phead = tp; 30 p1=p1->next; 31 p2=p2->next; 32 } 33 ListNode* pp=nullptr; 34 if(p1 != nullptr) 35 pp=p1; 36 if(p2 != nullptr) 37 pp=p2; 38 //处理长的某个非空链表的剩余部分(注意进位问题) 39 while(pp!=nullptr){ 40 temp = pp->val + flag; 41 if(temp>=10){ 42 flag =1; 43 temp = temp%10; 44 }else{ 45 flag = 0; 46 } 47 ListNode* tp = new ListNode(temp); 48 phead->next = tp; 49 phead = tp; 50 pp=pp->next; 51 } 52 //最高位是否需要进位 53 if(flag){ 54 ListNode* tp = new ListNode(flag); 55 phead->next = tp; 56 } 57 //注意链表的返回 58 return res->next; 59 } 60 };
注意:
定义新的链表的时候:是ListNode* res=new ListNode(0); 而不是ListNode* res=nullptr; (后一种情况,空指针,没有办法访问,res->val或者res->next)
前一种定义是正确的,返回是应该返回 res->next而不是res;
简洁版:

1 public ListNode addTwoNumbers2(ListNode l1, ListNode l2) { 2 ListNode dummyHead = new ListNode(0); 3 ListNode p = l1, q = l2, curr = dummyHead; 4 int carry = 0; 5 while (p != null || q != null) { 6 int x = (p != null) ? p.val : 0; 7 int y = (q != null) ? q.val : 0; 8 int sum = carry + x + y; 9 carry = sum / 10; 10 curr.next = new ListNode(sum % 10); 11 curr = curr.next; 12 if (p != null) p = p.next; 13 if (q != null) q = q.next; 14 } 15 if (carry > 0) { 16 curr.next = new ListNode(carry); 17 } 18 return dummyHead.next; 19 }
3. 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
解题思路-1:
使用队列、集合。集合用于判断是否出现重复元素。队列用于保存出现重复元素时,当前不重复的子串(将队首重复的元素,及之前的元素删掉)。

1 class Solution { 2 public: 3 int lengthOfLongestSubstring(string s) { 4 int sz = s.size(); 5 if(sz<2) 6 return sz; 7 8 set<char> setS; 9 queue<char> qS; 10 setS.insert(s[0]); 11 qS.push(s[0]); 12 int count = 1,temp=1; 13 for(int i=1;i<sz;i++){ //从索引1开始 14 auto iter = setS.find(s[i]); 15 if(iter!=setS.end()){ //找到元素,即出现相同元素 16 auto itQ = qS.front(); 17 while(itQ != s[i]){ 18 qS.pop(); 19 setS.erase(itQ); 20 temp--; 21 itQ = qS.front();//不要忘记更新变量,指向下一个元素 22 } 23 qS.pop(); // a b c a 集合与队列中已经有3个元素,对于集合,新来了a,其元素由啊a b c变为b c a。可以保持不变 24 qS.push(s[i]); //但对于队列,其设计顺序问题,若a b c保持不变(实际上是b c a),下一次进入时,a b c 会将a弹掉(错误) 25 }else{ //没有重复元素 26 qS.push(s[i]); 27 setS.insert(s[i]); 28 temp++; 29 } 30 count = max(count,temp); 31 } 32 return count; 33 } 34 }; 35 36 //队列没有迭代器,qS.begin()是错误的
注意:1)队列(queue)没有迭代器 2)当队列中元素是 a b c时,进入元素a,应该将对首a删除,然后队尾添加a,保持相邻元素的顺序。
解题思路-2:
上述思路使用队列消耗了多余的空间。实际上使用两个指针来表示当前无重复字符的子串即可以

1 class Solution { 2 public: 3 int lengthOfLongestSubstring(string s) { 4 int sz = s.size(); 5 if(sz<2) 6 return sz; 7 8 int start=0,end=1; 9 int count = end - start; 10 unordered_set<char> setS; 11 setS.insert(s[0]); 12 13 for(int i=1;i<sz;i++){ 14 if(setS.find(s[i])!=setS.end()){//找到重复元素 15 while(s[start]!=s[i]){ 16 setS.erase(s[start]); //不要忘记删除队首多余的元素 17 start++; 18 } 19 start++; //两者同时后移,因为while只处理了重复元素的前面的元素,而没有考虑之后的元素 20 end++; 21 }else{ 22 end++; 23 setS.insert(s[i]); 24 } 25 count = max(count,end-start); 26 27 } 28 return count; 29 } 30 };
4. 寻找两个有序数组的中位数🤣
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例1 nums1 = [1, 3] nums2 = [2] 则中位数是 2.0 示例2 nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
解题思路:
有复杂度O(log(m + n))可知,遍历一遍数组即可。当n为偶数时,中位数取中间的两个数(total/2,total/2+1)的平均数;当n为奇数的时候,中位数取中间的一个数(total/2+1)。此处指的不是数据在存储时的索引,而是第几个数。

1 class Solution { 2 public: 3 double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { 4 int sz1 = nums1.size(); 5 int sz2 = nums2.size(); 6 if(sz1 ==0 && sz2==0) 7 return 0.0; 8 9 int total = sz1+sz2; 10 11 bool flag = false; //标记中位数是1个数,还是取两个数的平均 12 if(total%2!=0) 13 flag=true; //奇数个 14 15 int mid = total/2+1; 16 17 int p1=0,p2=0,index=0; 18 vector<int> res; 19 while(p1<sz1 && p2<sz2){ //不能加等号,因为p1=sz1时,nums1[p1]超出了引用范围 20 if(nums1[p1]<nums2[p2]){ 21 p1++; 22 index++; 23 if(index==mid-1) 24 res.push_back(nums1[p1-1]); 25 if(index==mid){ 26 res.push_back(nums1[p1-1]); 27 break; 28 } 29 30 }else{ 31 p2++; 32 index++; 33 if(index==mid-1) 34 res.push_back(nums2[p2-1]); 35 if(index==mid){ 36 res.push_back(nums2[p2-1]); 37 break; 38 } 39 40 } 41 } 42 43 while(p1>=sz1 && p2<=sz2){ //为了能取到最后一个元素:有等号p2<=sz2 44 p2++; 45 index++; 46 if(index==mid-1) 47 res.push_back(nums2[p2-1]); 48 if(index==mid){ 49 res.push_back(nums2[p2-1]); 50 break; 51 } 52 } 53 while(p2>=sz2 && p1<=sz1){ 54 p1++; 55 index++; 56 if(index==mid-1) 57 res.push_back(nums1[p1-1]); 58 if(index==mid){ 59 res.push_back(nums1[p1-1]); 60 break; 61 } 62 } 63 64 if(res.size()==2 && flag==false) //偶数个 65 return (res[0]+res[1])/2.0; 66 67 if(res.size()==2 && flag==true){//奇数个 68 return double(res[1]); 69 } 70 71 return double(res[0]); //不能把所有的return都放在if中 72 } 73 };
5. 最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
输入: "babad" 输出: "bab" 注意: "aba" 也是一个有效答案。 输入: "cbbd" 输出: "bb"
解题思路:
遍历字符串,选择每个元素回文的中心(可能时偶数个,也可能是奇数个,要考虑两个方面)
然后以中心位置,向两端扩展

1 class Solution { 2 public: 3 string longestPalindrome(string s) { 4 if(s.size()<2) 5 return s; 6 string res; 7 int begin=0,end=0; 8 9 for(int i=0;i<s.size()-1;i++){ 10 getLongestCurr(s,i,i,begin,end); //回文串为奇数时 11 getLongestCurr(s,i,i+1,begin,end); //回文串为偶数时 12 } 13 14 return s.substr(begin,end-begin+1); 15 16 } 17 void getLongestCurr(string s,int i1,int i2,int& begin,int& end){ 18 int L=i1, R=i2; 19 while(L>=0 && R<s.size() && s[L]==s[R]){ 20 L--; 21 R++; 22 } 23 L++; 24 R--; 25 if((R-L)>(end-begin)){ 26 begin = L; 27 end = R; 28 } 29 return; 30 } 31 };
6. 正则表达式匹配(11)🤣
给定一个字符串 (s) 和一个字符模式 (p)。实现支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符。 '*' 匹配零个或多个前面的元素。
匹配应该覆盖整个字符串 (s) ,而不是部分字符串。
说明:
s可能为空,且只包含从a-z的小写字母。p可能为空,且只包含从a-z的小写字母,以及字符.和*。
示例 1:
输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "a*"
输出: true
解释: '*' 代表可匹配零个或多个前面的元素, 即可以匹配 'a' 。因此, 重复 'a' 一次, 字符串可变为 "aa"。
示例 3:
输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 'c' 可以不被重复, 'a' 可以被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出: false
解题思路-1:
递归:
p为空的时候,s必须为空;但是s为空时,p不一定为空。 a* (*表示出现1次时)
匹配时有三种情况:
1. 普通字符(相匹配:判断下一个字符,不匹配:返回false)
2,模式为'.',一定匹配,可以直接跳过。
3. 当前字符的下一个字符是*时:
考虑*出现0次
出现多次

1 /* 2 p为空的时候,s必须为空;但是s为空时,p不一定为空。 a* (*表示出现1次时) 3 匹配时有三种情况: 4 1. 普通字符(相匹配:判断下一个字符,不匹配:返回false) 5 2,模式为'.',一定匹配,可以直接跳过。 6 3. 当前字符的下一个字符是*时: 7 考虑*出现0次 8 出现多次 9 10 */ 11 class Solution { 12 public: 13 bool isMatch(string s, string p) { 14 if(p.size()<=0) 15 return s.size()<=0; 16 17 bool match = s.size()>0 && (s[0]==p[0] || p[0]=='.'); 18 19 if(p.size()>1 && p[1]=='*') 20 return isMatch( s, p.substr(2)) || (match && isMatch( s.substr(1), p)); 21 else 22 return match && isMatch( s.substr(1), p.substr(1)); 23 24 //return false; //存在与否,没有关系,都可以通过 25 } 26 };
解题思路-2:
实动态规划也是一种分治的思想,将问题分解成一个个子问题,通过解决所有子问题,来求得原问题的解,一般用于求解最优问题。
但是跟分治法不同的地方在于,动态规划的子问题往往是相互关联的。在分治的基础上加入了一个状态数组,来存储中间计算的结
果,以减少重复计算的耗时。 动态规划分为两种,一种是自顶向下,另一个种是自底向上。 在动态规划中有几个比较关键的概念:子问题,状态,状态空间,初始状态,状态转移方程。 子问题:与原问题形式相同或者类似,只不过规模变小了,子问题都解决后,原问题即解决。 状态:与子问题相关的各个变量的一组取值即为状态,状态与子问题是一对一或一对多的关系,代表着子问题的解。 状态空间:由所有状态构成的集合。 状态初始条件:即状态的初始状态。 状态转移方程:用来表示状态之间是如何转换的方程,即如何从一个或者多个已知的状态求出另一个状态,可以使用递推公式表示。
自顶向下:
自底向上:
7.盛最多水的容器(11)
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
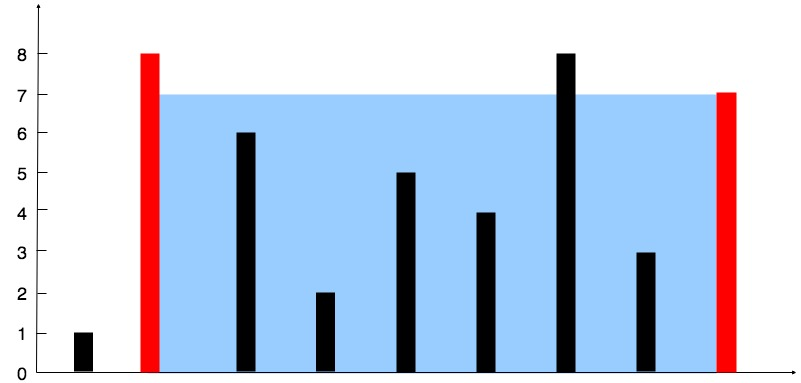
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例: 输入: [1,8,6,2,5,4,8,3,7] 输出: 49
解题思路:
双指针:首尾指针一点一点像内移动,每次移动首指针或者尾指针。距离一定减小,因此选高度大的,决定高度的是最短的线,因此每次移动短的线所对的指针。
area = min(height[i], height[j]) * (j - i)

1 class Solution { 2 public: 3 int maxArea(vector<int>& height) { 4 if(height.size()<2) 5 return 0; 6 7 int start = 0, end = height.size()-1; 8 int area=min(height[start],height[end])*(end-start); 9 while(start<end){ 10 if(height[start]<height[end]) 11 start++; 12 else 13 end--; 14 int temp = min(height[start],height[end])*(end-start); 15 area = max(area,temp); 16 } 17 return area; 18 19 } 20 };
8. 三数之和(15)
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4], 满足要求的三元组集合为: [ [-1, 0, 1], [-1, -1, 2] ]
解题思路:
转化成对两个数求和(等于指定值),选取一个元素(因为不重复,只选择负数或0即可),然后从剩下的元素中选择另两个元素(使用两个指针,不断向中间逼近)。
注意选取一个元素时,每次选择不重复的元素(while判断是否与之前的元素相等,相等则跳过,注意索引的范围是否在合理的值域)
选择另外两个元素时,当找到一组符合的值后,注意接下来招的值因该不重复,因此,两个指针移动时,不是简单的begin++,end--;而是begin一直找到不相等的元素(注意不要超出索引),end一直向前找到不重复的值(注意不要超出索引)。

1 class Solution { 2 public: 3 vector<vector<int>> threeSum(vector<int>& nums) { 4 int sz = nums.size(); 5 vector<vector<int>> res; 6 if(sz<3) 7 return res; 8 vector<int> line; 9 sort(nums.begin(),nums.end()); 10 11 for(int i=0;i<sz-2;i++){ 12 if(nums[i]<=0){//由于不重复,只处理负数与0即可。处理正数时,会与负数、0重复 13 //为了避免重复,相同的元素不再判断 14 while(i-1>=0 && i<sz && nums[i]==nums[i-1]){ 15 //注意范围的判断:因为要访问nums[i]与nums[i-1],要保证i与i-1在合理范围!!! 16 i++; 17 } 18 int begin=i+1,end=sz-1; 19 while(begin<end){ 20 int target = -nums[i]; 21 if(nums[begin]+nums[end]==target){ 22 line.push_back(nums[i]); 23 line.push_back(nums[begin]); 24 line.push_back(nums[end]); 25 res.push_back(line); 26 line.clear(); 27 //找到nums[begin],对nums[i]来说,该元素不可以再出现 28 //指针怎么走 29 int temp = nums[begin]; 30 while(begin<sz && nums[begin]==temp ){ //去除重复元素 31 //要访问nums[begin],因此保证索引begin在合理范围内 32 begin++; 33 } 34 temp = nums[end]; 35 while(end>i && nums[end]==temp){ //去除重复元素 36 //要访问nums[end],因此保证索引end在合理范围内 37 end--; 38 } 39 40 41 }else if(nums[begin]+nums[end]<target){ 42 begin++; 43 }else{ 44 end--; 45 } 46 47 } 48 49 } 50 } 51 52 return res; 53 } 54 /* 55 //不能将该函数单独写,因为不确定一次是找到一个vector<int>的还是多个vector<int>,无法拼接 56 vector<int> getTwo(vector<int>& nums,int begin,int end,int target){ 57 vector<int> res; 58 while(begin<end){ 59 if(nums[begin]+nums[end]==target){ 60 res.push_back(); 61 res.push_back(); 62 res.push_back(); 63 //没写完...... 64 } 65 } 66 67 }*/ 68 69 70 };
9.电话号码的字母组合(17)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例: 输入:"23" 输出:["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].
说明:
尽管上面的答案是按字典序排列的,但是你可以任意选择答案输出的顺序。
解题思路-1:
使用递归,回溯方法:🤣

1 //回溯 2 class Solution { 3 public: 4 vector<string> letterCombinations(string digits) { 5 vector<string> res; 6 7 if(digits.size()==0) 8 return res; 9 10 letterCombinationsCore( digits, res,"",0); 11 return res; 12 } 13 14 void letterCombinationsCore(string& digits, vector<string> & res,string prefix,int index){ 15 if(index>=digits.size()){ 16 res.push_back(prefix); 17 return; //递归终止,不要忘记return. 18 } 19 20 21 string chars = character[digits[index]-'2']; //digits[index]是一个字符,而不是数字 22 for(int i=0;i<chars.size();i++){ 23 letterCombinationsCore(digits, res, prefix+chars[i], index+1); 24 } 25 return; 26 } 27 28 private: 29 vector<string> character={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; 30 };
注意:digits[index]是一个字符,而不是数字。不能直接减2,应该减去'2'。
实现思路不对,代码写不下去了,吸取教训 (递归的,输入输出应该怎么处理)

1 //回溯 2 class Solution { 3 public: 4 vector<string> letterCombinations(string digits) { 5 vector<string> res; 6 letterCombinationsCore( digits, res); 7 return res; 8 } 9 10 string letterCombinationsCore(string digits, vector<string> & res){ 11 if(digits.size()==0) 12 return ""; 13 string chars = character[digits[0]-2]; 14 string temp; 15 for(int i=0;i<chars.size();i++){ 16 //在for循环中temp什么都不做,因此for循环结束后,temp取最后一个值,前面的都被覆盖了 17 if(digits.size()==1) 18 temp = chars[i]; //错误:在循环中,之前的结果会被覆盖!!! 19 else 20 temp = chars[i]+letterCombinationsCore(digits.substr(1),res); 21 22 if(digits.size()==temp.size()) 23 res.push_back(temp); 24 } 25 return temp; 26 } 27 28 private: 29 vector<string> character={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; 30 };
解题思路-2:
使用队列,添加标志flag隔开每位

1 //使用队列方法 2 class Solution { 3 public: 4 vector<string> letterCombinations(string digits) { 5 int sz = digits.size(); 6 vector<string> res; 7 if(sz==0) 8 return res; 9 10 queue<string> qS; 11 qS.push(""); //为了统一每次与之前得到的子串相加操作 12 qS.push("flag"); //标志:用于隔开每个digits位 13 14 for(int i=0;i<sz;i++){ 15 string temp = character[digits[i]-'2']; 16 while(qS.front()!="flag"){ 17 for(int j=0;j<temp.size();j++){ 18 //string t = temp[j]; //是char,不是string 19 qS.push(qS.front()+temp[j]); //注意索引是j而不是i 20 } 21 qS.pop(); 22 } 23 qS.push("flag");//添加新的标志 24 qS.pop(); //删除flag 25 26 } 27 /* 28 for(int i=0;i<sz;i++){ //返回结果处理错误,原字符串只有两个字符,如:"23",但返回结果会有6个!! 29 res.push_back(qS.front()); 30 qS.pop(); 31 }*/ 32 while(qS.front()!="flag"){ 33 res.push_back(qS.front()); 34 qS.pop(); 35 } 36 37 return res; 38 } 39 40 private: 41 vector<string> character={"abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; 42 };
10. 删除链表的倒数第N个节点(19)
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例: 给定一个链表: 1->2->3->4->5, 和 n = 2. 当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
解题思路:
使用双指针,一个指针(p1)先走n步,然后两个指针(p1,p2)同时走, 当p1走到链表尾节点时,p2走到要删除节点的父节点,根据父节点删除元素即可。
注意非法输入判定:删除倒数第n个节点,但是链表没有那么长,不用删除,直接返回节点即可。
注意边界:删除的链表是头节点、中间节点、以及尾节点的不同情况。(头节点单独考虑)

1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 //定义两个指针,一个提前走n步(找到要删除节点的父节点,根据父节点删除要删除的节点),然后两者同时走 10 class Solution { 11 public: 12 ListNode* removeNthFromEnd(ListNode* head, int n) { 13 if(head==nullptr) 14 return head; 15 16 ListNode* p1 = head; 17 ListNode* p2 = head; 18 19 while(p1->next!=nullptr && n>0){ 20 p1 = p1->next; 21 n--; 22 } 23 if(n==1 && p1->next==nullptr){ //删除的是头节点 24 head = head->next; 25 return head; 26 } 27 //链表不够长,删除的索引超出 28 if(n>0){ 29 return head; 30 } 31 32 while(p1->next!=nullptr){ 33 p1 = p1->next; 34 p2 = p2->next; 35 } 36 37 //删除p2指向的节点 38 //p2可能是头指针(前面处理)、中间节点的指针、尾节点的指针 39 ListNode* temp = p2->next; 40 p2->next = temp->next; //错误写法p2 = temp->next; 只是把p2指向temp->next,并没有改变原来的链表 41 delete temp; 42 43 return head; 44 45 } 46 };
11. 有效的括号(20)
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

1 示例 1: 2 3 输入: "()" 4 输出: true 5 示例 2: 6 7 输入: "()[]{}" 8 输出: true 9 示例 3: 10 11 输入: "(]" 12 输出: false 13 示例 4: 14 15 输入: "([)]" 16 输出: false 17 示例 5: 18 19 输入: "{[]}" 20 输出: true
解题思路:
1)实现1:
使用栈,左括号进栈,右括号时,判断栈顶元素是否是对应的左括号,是,弹出该元素,继续判断。不是,返回false。
注意:访问栈顶元素时,一定要保证,栈非空。否则会内存报错。

1 //使用栈 2 //"){" 3 class Solution { 4 public: 5 bool isValid(string s) { 6 int sz=s.size(); 7 if(sz==0 ) //注意空字符串,结果是true 8 return true; 9 if(sz%2==1){ //奇数个元素,结果false 10 return false; 11 } 12 stack<char> sta; 13 for(int i=0;i<sz;i++){ 14 if(s[i]=='(' || s[i]=='[' || s[i]=='{' ) 15 sta.push(s[i]); 16 else if (s[i]==')'){ 17 if(!sta.empty() && sta.top()=='('){ //if判断条件中,要访问sta.top()。,所以要保证sta非空 18 sta.pop(); 19 }else 20 return false; 21 }else if(!sta.empty() && s[i]==']'){ 22 if(sta.top()=='['){ 23 sta.pop(); 24 }else 25 return false; 26 }else if(!sta.empty() && s[i]=='}'){ 27 if(sta.top()=='{'){ 28 sta.pop(); 29 }else 30 return false; 31 } 32 } 33 if(sta.empty()) 34 return true; 35 36 return false; //要有该返回条件,否则会认为函数没有返回结果。因为上面只有if。如果是if else,就没关系。 37 } 38 };
2)实现2:(不用使用left、right计数)
用一个栈,我们开始遍历输入字符串,如果当前字符为左半边括号时,则将其压入栈中,如果遇到右半边括号时,若此时栈为空,则直接返回false,如不为空,则取出栈顶元素,若为对应的左半边括号,则继续循环,反之返回false

1 class Solution { 2 public: 3 bool isValid(string s) { 4 stack<char> parentheses; 5 for (int i = 0; i < s.size(); ++i) { 6 if (s[i] == '(' || s[i] == '[' || s[i] == '{') parentheses.push(s[i]); 7 else { 8 if (parentheses.empty()) return false; 9 if (s[i] == ')' && parentheses.top() != '(') return false; 10 if (s[i] == ']' && parentheses.top() != '[') return false; 11 if (s[i] == '}' && parentheses.top() != '{') return false; 12 parentheses.pop(); 13 } 14 } 15 return parentheses.empty(); 16 } 17 };
12. 合并两个有序链表(21)
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例: 输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4
解题思路:🤣
建立一个头节点,使头节点的连接与中间节点的连接操作统一。
建立一个临时指针,用于指向确定的当前节点,由该节点向下连接其他较小的节点。
不要忘记最后连接,剩下的某个链表的节点。

1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 /* 10 [5] 11 [1,2,4] 12 输出:[1,5] 正确的输出:[1,2,4,5] 13 */ 14 class Solution { 15 public: 16 ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { 17 if(l1==nullptr) 18 return l2; 19 if(l2==nullptr) 20 return l1; 21 22 ListNode* head = new ListNode(-1); //定义新的头节点,使头节点与中间节点的操作统一!! 23 ListNode* temp = head; 24 25 ListNode* p1 = l1; 26 ListNode* p2 = l2; 27 28 //连接两个链表 29 while(p1!=nullptr && p2!=nullptr){//不是p1->next!=nullptr 30 if(p1->val > p2->val){ //大于:选择p2 31 temp->next = p2; 32 p2 = p2->next; 33 temp = temp->next; 34 }else{ 35 temp->next = p1; 36 p1 = p1->next; 37 temp = temp->next; 38 } 39 } 40 //连接剩余的节点 41 if(p1!=nullptr){ //是if不是while 42 temp->next = p1; 43 } 44 if(p2!=nullptr){ 45 temp->next = p2; 46 } 47 48 return head->next; //返回head->next而不是head 49 50 } 51 };
错误的代码(思路错误:将临时指针放在后面)
[5]
[1,2,4]
输出:[1,5] 比较1与5,1比5小,就将1连在5的前面,没有考虑1后面的数(2,4)可能会比5更小。
正确的输出:[1,2,4,5]

1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode(int x) : val(x), next(NULL) {} 7 * }; 8 */ 9 /* 10 [5] 11 [1,2,4] 12 输出:[1,5] 正确的输出:[1,2,4,5] 13 */ 14 class Solution { 15 public: 16 ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) { 17 if(l1==nullptr) 18 return l2; 19 if(l2==nullptr) 20 return l1; 21 22 ListNode* head = nullptr; //头指针指向元素较小的节点 23 if(l1->val>l2->val){ 24 head = l2; 25 }else{ 26 head = l1; 27 } 28 29 ListNode* p1 = l1; 30 ListNode* p2 = l2; 31 ListNode* temp = nullptr; 32 //连接两个链表 33 while(p1!=nullptr && p2!=nullptr){//不是p1->next!=nullptr 34 if(p1->val > p2->val){ //大于:选择p2 35 temp = p2->next; 36 p2->next = p1; 37 p2 = temp; 38 }else{ 39 temp = p1->next; 40 p1->next = p2; 41 p1 = temp; 42 } 43 } 44 return head; 45 46 } 47 };
13. 括号生成(22)🤣
给出 n 代表生成括号的对数,请你写出一个函数,使其能够生成所有可能的并且有效的括号组合。
例如,给出 n = 3,生成结果为:
[ "((()))", "(()())", "(())()", "()(())", "()()()" ]
解题思路:
规律:定义左括号数=右括号数=n,当两者相等时,一定要使用左括号。当left<right时,使用左括号(非零时)或者右括号都可以。递归

1 //回溯算法 2 class Solution { 3 public: 4 vector<string> generateParenthesis(int n) { 5 vector<string> res; 6 if(n<1) 7 return res; 8 9 string s=""; 10 11 generateParenthesisCore(res, s, n, n); 12 13 return res; 14 } 15 16 void generateParenthesisCore(vector<string> &res, string after,int left,int right){ 17 if(left==0 && right==0){ 18 res.push_back(after); 19 return; 20 } 21 22 if(left==right){ 23 generateParenthesisCore(res, after+'(', left-1, right); 24 }else if(left<right){ 25 if(left!=0) 26 generateParenthesisCore(res, after+'(', left-1, right); 27 28 generateParenthesisCore(res, after+')', left, right-1); 29 30 } 31 32 return; 33 } 34 };
14. 合并K个排序链表(23)
合并 k 个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
示例: 输入: [ 1->4->5, 1->3->4, 2->6 ] 输出: 1->1->2->3->4->4->5->6
解题思路:
15. 下一个排列(31)
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
1,2,3 → 1,3,2 3,2,1 → 1,2,3 1,1,5 → 1,5,1
解题思路:
对数组从右到左查找,找到nums[i] 比nums[i+1]小的时候,就将nums[i]跟nums[i+1]到nums[nums.length - 1]当中找到一个最小的比nums[i]大的元素交换。
交换后,再把nums[i+1]到nums[nums.length-1]排序
注意找规律

1 class Solution { 2 public: 3 void nextPermutation(vector<int>& nums) { 4 int sz = nums.size(); 5 if(sz<2) 6 return; 7 int i=sz-2; 8 for(;i>=0;i--){ 9 if(nums[i]<nums[i+1]) 10 break; 11 } 12 13 if(i<0) 14 return reverse(nums.begin(),nums.end()); 15 16 int index = i+1; 17 for(int j=sz-1;j>i;j--){ 18 if(nums[j]>nums[i] && nums[j]<nums[index]){ 19 index = j; 20 } 21 } 22 23 swap(nums[i],nums[index]); 24 25 sort(nums.begin()+i+1,nums.end()); 26 27 return; 28 29 } 30 };
16. 最长有效括号(32)
给定一个只包含 '(' 和 ')' 的字符串,找出最长的包含有效括号的子串的长度。
示例 1: 输入: "(()" 输出: 2 解释: 最长有效括号子串为 "()" 示例 2: 输入: ")()())" 输出: 4 解释: 最长有效括号子串为 "()()"
解题思路-1:
1)使用栈 时间 O(N) 空间 O(N)
定义start变量来记录合法括号串的起始位置,遍历字符串,如果遇到左括号,则将当前下标压入栈;如果遇到右括号,如果当前栈为空,则将下一个坐标位置记录到start,如果栈不为空,则将栈顶元素取出,此时若栈为空,则更新结果和i - start + 1中的较大值,否则更新结果和i - 栈顶元素中的较大值。

1 class Solution { 2 public: 3 int longestValidParentheses(string s) { 4 int sz = s.size(); 5 if(sz<2) 6 return 0; 7 8 9 stack<int> sta; //用于存取左括号的索引 10 int start = 0, maxV=0; 11 for(int i=0;i<sz;i++){ 12 if(s[i]=='('){ 13 sta.push(i); 14 }else{ 15 if(sta.empty()) 16 start = i+1; 17 else{ //非空,则栈中一定存在左括号 18 sta.pop(); 19 maxV = sta.empty()? max(maxV, i-start+1):max(maxV, i-sta.top()); 20 } 21 } 22 } 23 return maxV; 24 } 25 };
解题思路-2:
2)一维动态规划逆向求解 时间 O(N) 空间 O(N)
dp[i]表示从s[i]到s[s.length - 1] 包含s[i] 的最长的有效匹配括号子串长度。
如果s[i]是右括号,因为不可能有右括号开头的括号对,所以d[i] = 0。
- dp[s.length - 1] = 0;
- i从n - 2 -> 0逆向求dp[],并记录其最大值。若s[i] == '(',则在s中从i开始到s.length - 1计算dp[i]的值。这个计算分为两步,通过dp[i + 1]进行的(注意dp[i + 1]已经在上一步求解): 在s中寻找从i + 1开始的有效括号匹配子串长度,即dp[i + 1],跳过这段有效的括号子串,查看下一个字符,其下标为j = i + 1 + dp[i + 1]。若j没有越界,并且s[j] == ‘)’,则s[i ... j]为有效括号匹配,dp[i] =dp[i + 1] + 2。
- 在求得了s[i ... j]的有效匹配长度之后,若j + 1没有越界,则dp[i]的值还要加上从j + 1开始的最长有效匹配,即dp[j + 1]。

1 class Solution { 2 public: 3 int longestValidParentheses(string s) { 4 int len = s.length(); 5 if(len<2) 6 return 0; 7 int max = 0; 8 int *dp = new int[len]; 9 for(int k = 0;k<len;k++)//把辅助数组清空,存储为0 10 dp[k] = 0; 11 for(int i = len-2;i>=0;i--) 12 { 13 if(s[i] == '(')//只对左括号处理,右括号在数组中存储为0 14 { 15 int j = i+1+dp[i+1];//计算与当前左括号匹配的右括号的位置。可能存在也可能不存在 16 if(j<len && s[j] == ')')//确保位置不能越界 17 { 18 dp[i] = dp[i+1] + 2;//找到了相匹配的右括号,当前数组中存储的最长长度是它后一个位置加2,后一个位置可能存储长度是0 19 if(j+1<len)//这是连接两个子匹配的关键步骤 20 dp[i] += dp[j+1];//在j的后面可能已经存在连续的匹配,要记得加上。dp[j+1]存储了以j+1开始的匹配 21 } 22 if(dp[i]>max) 23 max = dp[i];//更新最长长度 24 } 25 26 } 27 return max; 28 } 29 };
考虑问题不全,错误的求解方法:

1 //动态规划 2 //"()(()" //正确输出是2,本方法的输出是4 没有考虑连续字串的最长有效 3 class Solution { 4 public: 5 int longestValidParentheses(string s) { 6 int sz = s.size(); 7 if(sz<2) 8 return 0; 9 int maxV = 0; 10 int left = 0, right = 0; 11 for(int i=0;i<sz;i++){ 12 if(s[i]=='(') 13 left++; 14 else 15 right++; 16 if(right>left){ 17 left=0; 18 right=0; 19 }else{ 20 maxV = max(maxV,right*2); 21 } 22 } 23 24 return maxV; 25 } 26 };

1 //动态规划 2 //"(()" //正确输出是2,本方法的输出是0 没有考虑连续字串的最长有效 3 class Solution { 4 public: 5 int longestValidParentheses(string s) { 6 int sz = s.size(); 7 if(sz<2) 8 return 0; 9 int maxV = 0; 10 int left = 0, right = 0; 11 int start = 0; 12 stack<char> sta; 13 bool flag = false; 14 for(int i=0;i<sz;i++){ 15 16 if(s[i]=='('){ 17 left++; 18 sta.push(s[i]); 19 20 }else{ 21 right++; 22 if(!sta.empty() && sta.top()=='('){ //栈非空才能访问栈顶 23 sta.pop(); 24 }else{ 25 flag = true; 26 } 27 } 28 if(right>left || flag){ 29 left==0; 30 right==0; 31 32 flag = false; 33 maxV = max(maxV, i-start); 34 start==i+1; 35 } 36 37 } 38 39 return maxV; 40 } 41 };
17. 搜索旋转排序数组(33)
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1: 输入: nums = [4,5,6,7,0,1,2], target = 0 输出: 4 示例 2: 输入: nums = [4,5,6,7,0,1,2], target = 3 输出: -1
解题思路:
使用二分查找,重点是怎么判断选择中间点的左边还是右边:
对于数组[0 1 2 4 5 6 7] 共有下列七种旋转方法:
0 1 2 4 5 6 7
7 0 1 2 4 5 6
6 7 0 1 2 4 5
5 6 7 0 1 2 4
4 5 6 7 0 1 2
2 4 5 6 7 0 1
1 2 4 5 6 7 0
可以观察出规律,如果中间的数小于最右边的数,则右半段是有序的,若中间数大于最右边数,则左半段是有序的
只要在有序的半段里用首尾两个数组来判断目标值是否在这一区域内,这样就可以确定保留哪半边了 ref

1 class Solution { 2 public: 3 int search(vector<int>& nums, int target) { 4 int sz = nums.size(); 5 if(sz<1) 6 return -1; 7 8 int start = 0,end = sz-1; 9 int res=-1; 10 while(start<=end){ 11 int mid = (start+end)/2; 12 if(target==nums[mid]){ 13 return mid; 14 }else if(nums[mid]<=nums[end] ){ //右边的数组有序 15 if(target>nums[mid] && target<=nums[end]) 16 start = mid+1; 17 else 18 end = mid-1; 19 }else { //左边的数组有序 20 if((target>=nums[start]) && (target<nums[mid])) 21 end = mid-1; 22 else 23 start = mid+1; 24 } 25 } 26 27 return res; 28 29 } 30 };
18. 在排序数组中查找元素的第一个和最后一个位置(34)
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1: 输入: nums = [5,7,7,8,8,10], target = 8 输出: [3,4] 示例 2: 输入: nums = [5,7,7,8,8,10], target = 6 输出: [-1,-1]
解题思路-1:
1) 不建议,时间复杂度与数组有关。不能满足log(n)
二分查找找到中间的数字,由于相同的元素连续放置。用while循环在左右查找相同的元素
缺点:如果数组都是相同的元素,用O(1)找到中间元素,之后会遍历左右元素确定范围O(n)

1 class Solution { 2 public: 3 vector<int> searchRange(vector<int>& nums, int target) { 4 int sz = nums.size(); 5 vector<int> res={-1,-1}; 6 if(sz<1) 7 return res; 8 9 int start=0,end=sz-1; 10 int curr=-1; 11 while(start<=end){ 12 int mid = (start+end)/2; 13 if(target==nums[mid]){ 14 curr=mid; 15 break; 16 }else if(target<nums[mid]){ 17 end = mid-1; 18 }else{ 19 start = mid+1; 20 } 21 } 22 if(curr==-1) 23 return res; 24 else{ 25 start = curr; 26 end = curr; 27 while(start-1>=0 && nums[start-1]==nums[curr]) 28 start--; 29 while(end+1<sz && nums[end+1]==nums[curr]) 30 end++; 31 32 } 33 res[0]=start; 34 res[1]=end; 35 36 return res; 37 } 38 };
解题思路-2:🤣
2) 使用两次二分查找法,第一次找到左边界,第二次调用找到右边界即可 ref

1 class Solution { 2 public: 3 vector<int> searchRange(vector<int>& nums, int target) { 4 int sz = nums.size(); 5 vector<int> res(2,-1); 6 if(sz<1) 7 return res; 8 9 int start=0,end=sz-1; 10 11 //先找左边界 12 while(start<end){ 13 int mid = (start+end)/2; 14 if(target>nums[mid]) 15 start = mid + 1; //+1后可能等于或小于target。向target逼近 16 else 17 end = mid; //不能有-1。此时是相等或者大于,相等时-1可能会变小。避开了相等值 18 } 19 20 if(nums[start]!=target) //判断是否找到元素。 21 return res; 22 res[0]=start; 23 24 //找右边界 25 end=sz; //如果是end=sz-1;会报错 26 /* 27 end=sz-1; 28 输入[1] 1 正确输出是[0,0] 29 该程序输出[0,-1] 30 */ 31 while(start<end){ 32 int mid = (start+end)/2; 33 if(target>=nums[mid]) 34 start = mid + 1; //start逼近第一个比target大的数。因此最终结果要减1 35 else 36 end = mid; // 37 } 38 39 /* 40 while(start<end){ 41 int mid = (start+end)/2; 42 if(target<nums[mid]) 43 end = mid -1; 44 else 45 start = mid; //会在此处陷入死循环!!! 46 } 47 res[1]=start; 48 */ 49 res[1]=start-1; //要减去1!!! 50 51 return res; 52 } 53 };
注意:查找时,总是从左侧逼近target(start),第一次<,第二次<=。
19. 组合总和(39)
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括
target)都是正整数。 - 解集不能包含重复的组合。
示例 1: 输入: candidates = [2,3,6,7], target = 7, 所求解集为: [ [7], [2,2,3] ] 示例 2: 输入: candidates = [2,3,5], target = 8, 所求解集为: [ [2,2,2,2], [2,3,3], [3,5] ]
解题思路:
使用递归:ref
像这种结果要求返回所有符合要求解的题十有八九都是要利用到递归,而且解题的思路都大同小异,相类似的题目有 Path Sum II,Subsets II,Permutations,Permutations II,Combinations 等等,如果仔细研究这些题目发现都是一个套路,都是需要另写一个递归函数,这里新加入三个变量,start记录当前的递归到的下标,out为一个解,res保存所有已经得到的解,每次调用新的递归函数时,此时的target要减去当前数组的数。
20. 接雨水(42)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例: 输入: [0,1,0,2,1,0,1,3,2,1,2,1] 输出: 6
解题思路:
21. 全排列(46)
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例: 输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
解题思路:
22. 旋转图像(48)
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1: 给定 matrix = [ [1,2,3], [4,5,6], [7,8,9] ], 原地旋转输入矩阵,使其变为: [ [7,4,1], [8,5,2], [9,6,3] ] 示例 2: 给定 matrix = [ [ 5, 1, 9,11], [ 2, 4, 8,10], [13, 3, 6, 7], [15,14,12,16] ], 原地旋转输入矩阵,使其变为: [ [15,13, 2, 5], [14, 3, 4, 1], [12, 6, 8, 9], [16, 7,10,11] ]
解题思路:
23. 字母异位词分组(49)
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
示例: 输入: ["eat", "tea", "tan", "ate", "nat", "bat"], 输出: [ ["ate","eat","tea"], ["nat","tan"], ["bat"] ]
说明:
- 所有输入均为小写字母。
- 不考虑答案输出的顺序。
解题思路:
24. 最大子序和(53)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例: 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
解题思路:

1 class Solution { 2 public: 3 int maxSubArray(vector<int>& nums) { 4 int sz = nums.size(); 5 if(sz<1) 6 return 0; 7 8 int maxV = nums[0]; 9 int currV = nums[0]; 10 for(int i=1;i<sz;i++){ 11 if(currV<0){ 12 currV = nums[i]; 13 }else{ 14 currV += nums[i]; 15 } 16 17 maxV = max(maxV,currV); 18 } 19 return maxV; 20 } 21 };
25. 跳跃游戏(55)
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
示例 1: 输入: [2,3,1,1,4] 输出: true 解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。 示例 2: 输入: [3,2,1,0,4] 输出: false 解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
解题思路:




