大话数据结构 -07-3 最小生成树
最小生成树
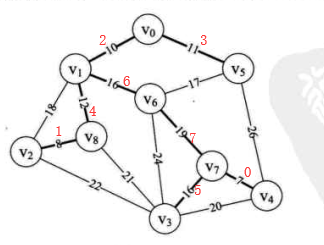
一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。
把构造连通网的最小代价生成树称为最小的生成树。(最小成本,即n个顶点,用n-1条边把一个连通图连接起来,并且使得权值的和最小)
经典算法:普里姆算法和克鲁斯卡尔算法
一、普里姆算法(Prim)
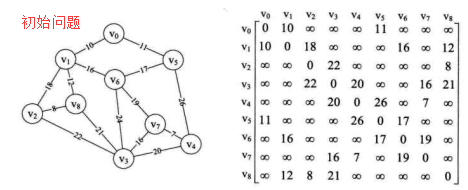
初始化工作:

构造最小生成树

第一次大循环,从v0开始,找到了第一个与v0权重最小所对应的顶点,并更新了lowcost(之前记录的是邻接矩阵的第一行,大循环后更新了找到的权值最小顶点所对应的邻接矩阵的行)
k=1,lowcost[1]=0(说明该顶点加入最小生成树) 更新后:lowcost={0,0,18,65535,65535,11,16,65535,12} adjvex={0,0,1,0,0,0,1,0,1}
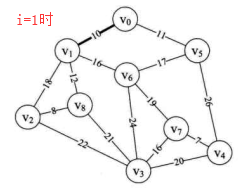
i=2时,min=11,k=5,lowcost[5]=0 (将顶点5加入生成树)。
连接边由(adjvex[k],k)定义,即(0,5) 其中 adjvex[5]=0。
用邻接矩阵的第五行更新lowcost={0,0,18,65535,26,0,16,65535,12} adjvex={0,0,1,0,5,0,1,0,1}
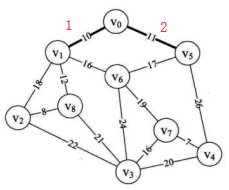
i=3时,min =12,k=8,lowcost[8]=0 (将顶点8加入生成树)。
连接边由(adjvex[k],k)定义,即(1,8) 其中 adjvex[8]=1
用邻接矩阵的第8行更新lowcost={0,0,8,21,26,0,16,65535,0} adjvex={0,0,8,8,5,0,1,0,1}
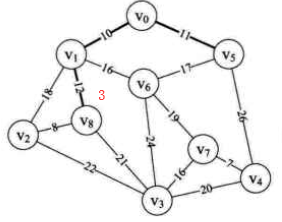
i=4时,min =8,k=2,lowcost[2]=0 (将顶点2加入生成树)。
连接边由(adjvex[k],k)定义,即(8,2) 其中 adjvex[2]=8
用邻接矩阵的第2行更新lowcost={0,0,0,21,26,0,16,65535,0} adjvex={0,0,8,8,5,0,1,0,1} 没有更新,第二行元素都比当前lowcost大
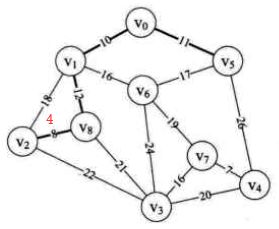
i=5时,min =16,k=6,lowcost[6]=0 (将顶点2加入生成树)。
连接边由(adjvex[k],k)定义,即(1,6) 其中 adjvex[6]=1
用邻接矩阵的第6行更新lowcost={0,0,0,21,26,0,0,19,0} adjvex={0,0,8,8,5,0,1,6,1}
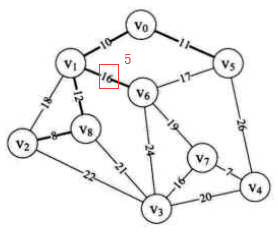
i=6时,min =19,k=7,lowcost[7]=0 (将顶点2加入生成树)。
连接边由(adjvex[k],k)定义,即(6,7) 其中 adjvex[7]=6
用邻接矩阵的第7行更新lowcost={0,0,0,16,7,0,0,0,0} adjvex={0,0,8,7,7,0,1,6,1}
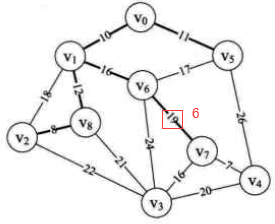
i=7时,min =7,k=4,lowcost[4]=0 (将顶点2加入生成树)。
连接边由(adjvex[k],k)定义,即(7,4) 其中 adjvex[4]=7
用邻接矩阵的第4行更新lowcost={0,0,0,16,0,0,0,0,0} adjvex={0,0,8,7,7,0,1,6,1}

i=8时,min =16,k=3,lowcost[3]=0 (将顶点2加入生成树)。
连接边由(adjvex[k],k)定义,即(7,3) 其中 adjvex[3]=7
用邻接矩阵的第3行更新lowcost={0,0,0,0,0,0,0,0,0} adjvex={0,0,8,7,7,0,1,6,1}

换一种思路理解,如下:(非常重要)有助于理解代码,为什么建立两个数组lowcost和adjvex。


二、克鲁斯卡尔算法(Kruskal)
因为权值在边上,直接去找最小权值的边来构建生成树,但构建时要考虑是否会形成环路。

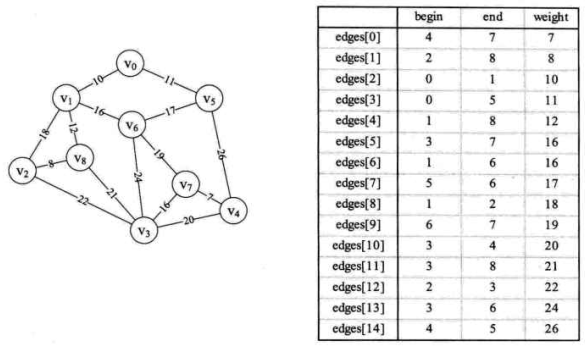
使用边集数组存储,并按权值大小排序


定义find函数:

程序运行:
i=0; begin=4;parent[4]=0,return 4,所以n=4;end=7;parent[7]=0,return 7,所以m=7;m!=n,更新parent[4]=7; 连接边(4,7)加入生成树中
i=1; begin=2;parent[2]=0,return 2,所以n=2;end=8;parent[8]=0,return 8,所以m=8;m!=n,更新parent[2]=8; 连接边(2,8)加入生成树中
i=2; begin=0;parent[0]=0,return 0,所以n=0;end=1;parent[1]=0,return 1,所以m=1;m!=n,更新parent[0]=1; 连接边(0,1)加入生成树中
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 0 | 8 | 0 | 7 | 0 | 0 | 0 | 0 |
i=3; begin=0;parent[0]=1>0,f=parent[0]=1,parent[1]=0;return 1,所以n=1;end=5;parent[5]=0,return 5,所以m=5;m!=n,更新parent[1]=5; 连接边(0,1)加入生成树中
(0已经与1相连,因此将与0相连的5放置再位置1)
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 8 | 0 | 7 | 0 | 0 | 0 | 0 |
i=4; begin=1;parent[1]=5,parent[5]=0,return 5,所以n=5;end=8;parent[8]=0,return 8,所以m=8;m!=n,更新parent[5]=8; 连接边(1,8)加入生成树中
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 8 | 0 | 7 | 8 | 0 | 0 | 0 |
i=5; begin=3;parent[3]=0,return 3,所以n=3;end=7;parent[7]=0,return 7,所以m=7;m!=n,更新parent[3]=7; 连接边(3,7)加入生成树中
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 8 | 7 | 7 | 8 | 0 | 0 | 0 |
i=6; begin=1;parent[8]=0,return 8,所以n=8;end=6;parent[6]=0,return 6,所以m=6;m!=n,更新parent[8]=6; 连接边(1,6)加入生成树中
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 8 | 7 | 7 | 8 | 0 | 0 | 6 |
i=7; begin=5;parent[6]=0,return 6,所以n=6;end=6;parent[6]=0,return 6,所以m=6;m==n,直接跳到下一个i循环。相等是因为边(5,6)形成了循环。
i=8; begin=1;parent[6]=0,return 6,所以n=6;end=2;parent[6]=0,return 6,所以m=6;m==n,直接跳到下一个i循环。相等是因为边(1,2)形成了循环。
i=9; begin=6;parent[6]=0,return 6,所以n=6;end=7;parent[7]=0,return 7,所以m=7;m!=n,更新parent[6]=7; 连接边(6,7)加入生成树中
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 5 | 8 | 7 | 7 | 8 | 7 | 0 | 6 |
此后的循环均造成环路。