10-01 斐波那契数列

题目描述：

 大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。n<=39

 

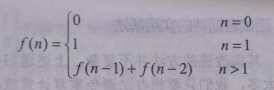
测试用例：

 1) 功能测试（3、5、10）

 2) 边界值测试（0、1、2）

 3) 性能测试（较大的数字：40、50、100）

 4) 错误输入：负值（-1、-2）

 

解题思路与代码：

 1) 根据公式，简单使用递归实现。 缺点：效率低下，n只能取较小的值

有两端特殊的区间：<0部分，0与1返回其本身，>1递归调用

class Solution {
public:
    int Fibonacci(int n) {
        int res = 0;
        if(n<0) //小于0，直接返回
            return 0;
        else if(n<2){
            res = n;
        }else{
            res = Fibonacci( n-1)+Fibonacci( n-2);
        }
        return res;
    }
};　　//
//在牛课上运行，显示：运行超时:您的程序未能在规定时间内运行结束，请检查是否循环有错或算法复杂度过大。case通过率为0.00%

//对上述时间超出要求的代码进行改进
class Solution {
public:
    int Fibonacci(int n) {
        //int res = 0;
        if(n<=0) //小于0，直接返回
            return 0;
        else if(n<=2){  //少一步f2的递归计算，时间上就可以通过 //if(n==1||n==2) return 1;
            return 1;
        }else{
            return Fibonacci( n-1)+Fibonacci( n-2);
        }
        //return res;
    }
}; //687ms
   //f2=1;直接给出结果，而不是通过f2=f1+f0计算即可满足时间要求　　　　

//使用递归方法
class Solution {
public:
    int Fibonacci(int n) {
        if(n==0)
            return 0;
        else if(n==1||n==2)
            return 1;
        else if(n==3)
            return 2;
        else
            return 3*Fibonacci(n-3)+2*Fibonacci(n-4);
        return 0; //n为负值时，直接返回0
    }
};
//f0=0; f1=1; f2=1; f3=2;
//f4=f3+f2=2*f2+f1=3*f1+2*f0
//f5=f4+f3=2*f3+f2=3*f2+2*f1
//每次递归比普通的递归少了几次重复值的计算，对于n偏大时仍然效率低

注意：该方法的时间复杂度是以n的指数方式递增的

 2）从下往上，利用已经求解过的值计算

 如 f8=f7+f6; 当计算f9时利用上一步的计算结果(f8)加上f7(相加较大的内个值)

class Solution {
public:
    int Fibonacci(int n) {
        if(n<=0)
            return 0;
        if(n==1)
            return 1;
        long long fibRes = 0;
        long long fibOne = 0;
        long long fibTwo = 1;
        for(int i=2;i<=n;i++){ //使用循环
            fibRes = fibOne + fibTwo;
            fibOne = fibTwo;
            fibTwo = fibRes;
        }
        return fibRes;
    }
};

3）动态规划，本质上同方法2一致，只是代码更简洁

class Solution {
public:
    int Fibonacci(int n) {
        int f = 0, g = 1;
        while(n--) { //循环n次
            g += f;
            //用更新后的g减去f，得到的是未更新前的g。
            //int temp=g; g=g+f; f=temp;
            f = g - f; 
        }
        return f;
        //为什么返回的是f而不是g。
        //写几个n观察，其中g表示f(n+1), f表示f(n)
    }
};
//上述方法没有考虑输入为负值的时候，当n为负值时，while的条件判断为true,--后仍然为负值，会形成无限循环。
class Solution {
public:
    int Fibonacci(int n) {
        int f = 0, g = 1;
        if(n<0) //要考虑是否为负数，n为负时，while会陷入死循环
            return 0;
        while(n--) { //循环n次
            g += f;
            //用更新后的g减去f，得到的是未更新前的g。
            //int temp=g; g=g+f; f=temp;
            f = g - f; 
        }
        return f;
        //为什么返回的是f而不是g。
        //写几个n观察，其中g表示f(n+1), f表示f(n)
    }
};
或者 修改 while(n-- > 0)

4）简单的动态规划，以一定的空间代价避免代价更大的重复计算的栈空间浪费

class Solution {
public:
    int Fibonacci(int n) {
        if (n<=0)
            return 0;
        if(n==1){
            return 1;
        }
        //int[] record = new int[n+1];
        int *record = new int[n+1]; //占用一定的空间
        record[0] = 0;
        record[1] = 1;
        for(int i=2;i<=n;i++){
            record[i] = record[i-1] + record[i-2];
        }
        return record[n];
    }
}; 

空间浪费了sizeof(int)*(n-1)，时间复杂度也达到了O(n)。　

5) 矩阵的快速幂（p76）　　

　　

 

基础知识：