包含min函数的栈 & 滑动窗口最大值

1.包含min函数的栈

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

 解析：

对于普通栈的push()和pop()函数的复杂度为O(1)；而获取最小值的min() 函数需要遍历整个栈，复杂度为 O(N)。

本题的难点在于如何保证min()函数复杂度降维O(1)。

可借助辅助栈实现：

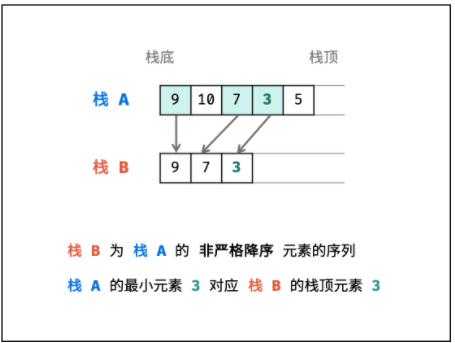
数据栈 A ： 栈 A 用于存储所有元素，保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。

辅助栈 B ： 栈 B 中存储栈 A 中所有 非严格降序 元素的子序列，则栈 A 中的最小元素始终对应栈 B 的栈顶元素。此时，min() 函数只需返回栈 B 的栈顶元素

因此，只需设法维护好 栈 B 的元素，使其保持是栈 A 的非严格降序元素的子序列，即可实现 min() 函数的 O(1) 复杂度。

 函数设计：

　　1.push(x)函数：对A push操作的同时也要对B push操作，重点保证栈B的元素非是非严格降序的

• • 执行元素x压入栈A
  • 若栈B为空或x<=栈B的栈顶元素，则执行元素x压入栈B

　　2.pop()函数：重点为保持栈A，栈B的元素一致性，始终让栈B中栈顶的元素是当前栈A中元素的最小值

• • 　执行栈A元素出栈，将出栈元素记为y
  • 　若y等于栈B的栈顶元素，则执行栈B元素出栈

　　3.top() 函数： 直接返回栈 A 的栈顶元素，即返回 A.peek() ；

　　4.min() 函数： 直接返回栈 B 的栈顶元素，即返回 B.peek() ；

python

class MinStack:
    def __init__(self):
        self.A, self.B = [], []

    def push(self, x: int) -> None:
        self.A.append(x)
        if not self.B or self.B[-1] >= x:
            self.B.append(x)

    def pop(self) -> None:
        if self.A.pop() == self.B[-1]:
            self.B.pop()

    def top(self) -> int:
        return self.A[-1]

    def min(self) -> int:
        return self.B[-1]

　　Java

class MinStack {
    Stack<Integer> A, B;
    public MinStack() {
        A = new Stack<>();
        B = new Stack<>();
    }
    public void push(int x) {
        A.add(x);
        if(B.empty() || B.peek() >= x)
            B.add(x);
    }
    public void pop() {
        if(A.pop().equals(B.peek()))
            B.pop();
    }
    public int top() {
        return A.peek();
    }
    public int min() {
        return B.peek();
    }
}

2.滑动窗口最大值

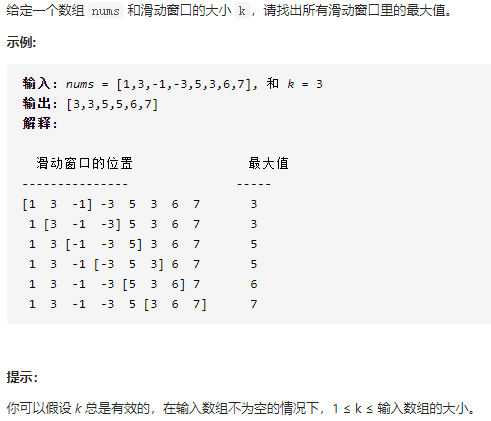
 解析：

本题与包含min函数的栈这个题目的区别在于“出栈操作”删除的“列表尾部元素”，“滑动窗口”删除的是“列表首部元素”

 

 

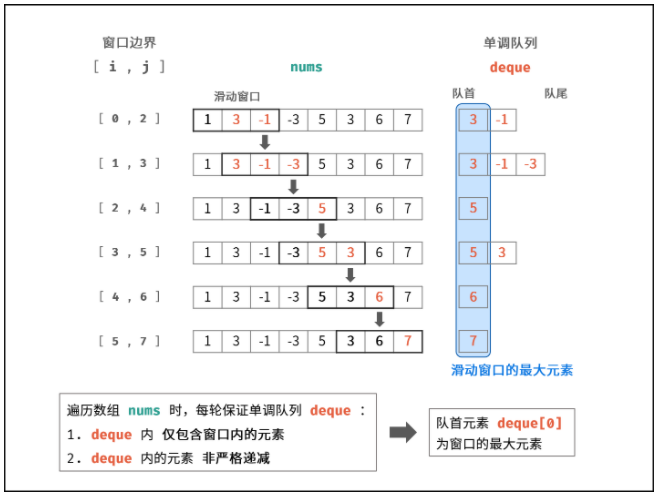
本题使用 单调队列 即可解决以上问题。遍历数组时，每轮保证单调队列 deque ：

deque 内 仅包含窗口内的元素⇒ 每轮窗口滑动移除了元素 nums[i - 1]，需将 deque内的对应元素一起删除。
deque 内的元素 非严格递减 ⇒ 每轮窗口滑动添加了元素 nums[j + 1]，需将 deque内所有 < nums[j + 1] 的元素删除。

 

 python

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        if not nums or k == 0:
            return []
        
        deque = collections.deque()
        # 未形成窗口前
        for i in range(k):
            while deque and deque[-1] < nums[i]:  # 保证队首是最大的
                deque.pop()
            deque.append(nums[i])

        res = [deque[0]]

        # 形成窗口后
        for i in range(k, len(nums)):
            if deque[0] == nums[i-k]:  # 将队首等于已删除的元素去掉
                deque.popleft()
            while deque and deque[-1] < nums[i]:
                deque.pop()
            deque.append(nums[i])
            res.append(deque[0])
        return res

　　Java

// 单调队列的实现
class MonotonicQueue {
    LinkedList<Integer> q = new LinkedList<>();
    public void push(int n) {
        // 将比n小的元素全部删除，保持队列的头是最大的
        while (!q.isEmpty() && q.getLast() < n) {
            q.pollLast();
        }
        // 将n加入尾部
        q.addLast(n);
    }

    // 前面的push方法已经保证了队列的头是最大的，因此获取最大值，只需获取队列的头部就行了
    public int max() {
        return q.getFirst();
    }

    // 删除队列头的元素，这里的删除，是遇到新加的数字与队列头的数字相同的情况
    public void pop(int n) {
        if (n == q.getFirst()) {
            q.pollFirst();
        }
    }
}

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        MonotonicQueue window = new MonotonicQueue();
        // 集合
        List<Integer> res = new ArrayList<>();

        for (int i=0; i < nums.length; i++) {
            if (i < k-1) {
                // 先填满窗口的前k-1
                window.push(nums[i]);
            } else {
                // 窗口向前滑动,加入新数字
                window.push(nums[i]);
                // 获取窗口中的最大值
                res.add(window.max());
                // 弹出旧的数字（这个旧数字如果与新的数字相同）
                window.pop(nums[i-k+1]);
            }
        }

        // 返回值要求的是返回数组int[]
        int[] arr = new int[res.size()];
        for(int i=0; i < res.size(); i++) {
            arr[i] = res.get(i);
        }

        return arr;

    }
}

　　参考：

https://leetcode-cn.com/leetbook/read/illustration-of-algorithm/58o46i/