梯度下降法推导,凸函数,收敛性推导
1.梯度下降法的收敛性
针对迭代式算法,我们就要Convergency Analysis(收敛性分析)
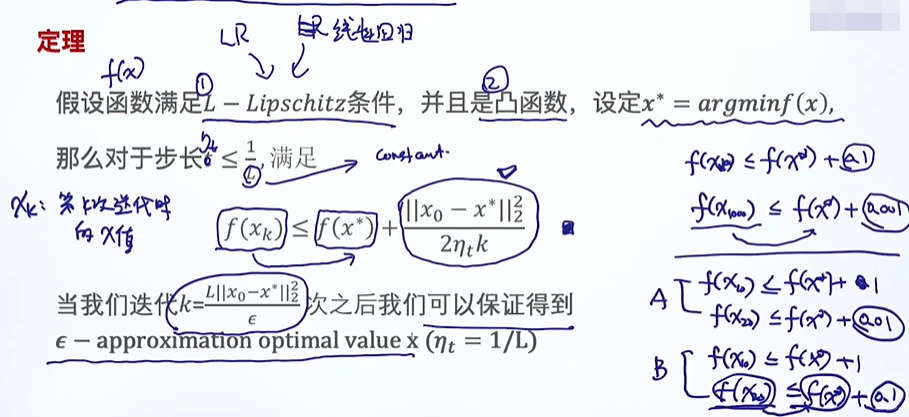
(1)什么是平滑函数,非平滑函数?
平滑函数--在每个点上求出梯度
非平滑函数---在那个点上求不出梯度的,
L-Lipschitz条件:是针对平滑函数的条件
Logistic Regression ,Linear Regression都是满足L-Lipschitz条件的
线性回归和逻辑回归都是凸函数
f(x*)是最终的收敛后的解,代表的最终想达到的最小值
我们的目标是通过学习的方式,使得f(xk)慢慢的接近f(x*),即
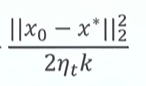
这一项如果随着迭代次数的增加(梯度下降法),慢慢的变小,就等同于f(xk)慢慢的接近f(x*)。
如果这一项的变小的趋势非常快,代表梯度下降法比较优质,而且很快可以收敛。
一个好的算法,在有限的最好的次数之内,可以看到A算法,在20次迭代,f(xk)接近f(x*)的速度比较快。
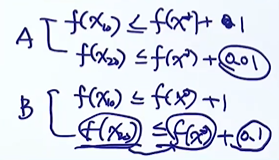
ε表示k次迭代,真实的值与预测值之间只存在ε的差距
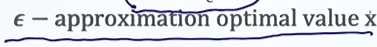
推导过程:
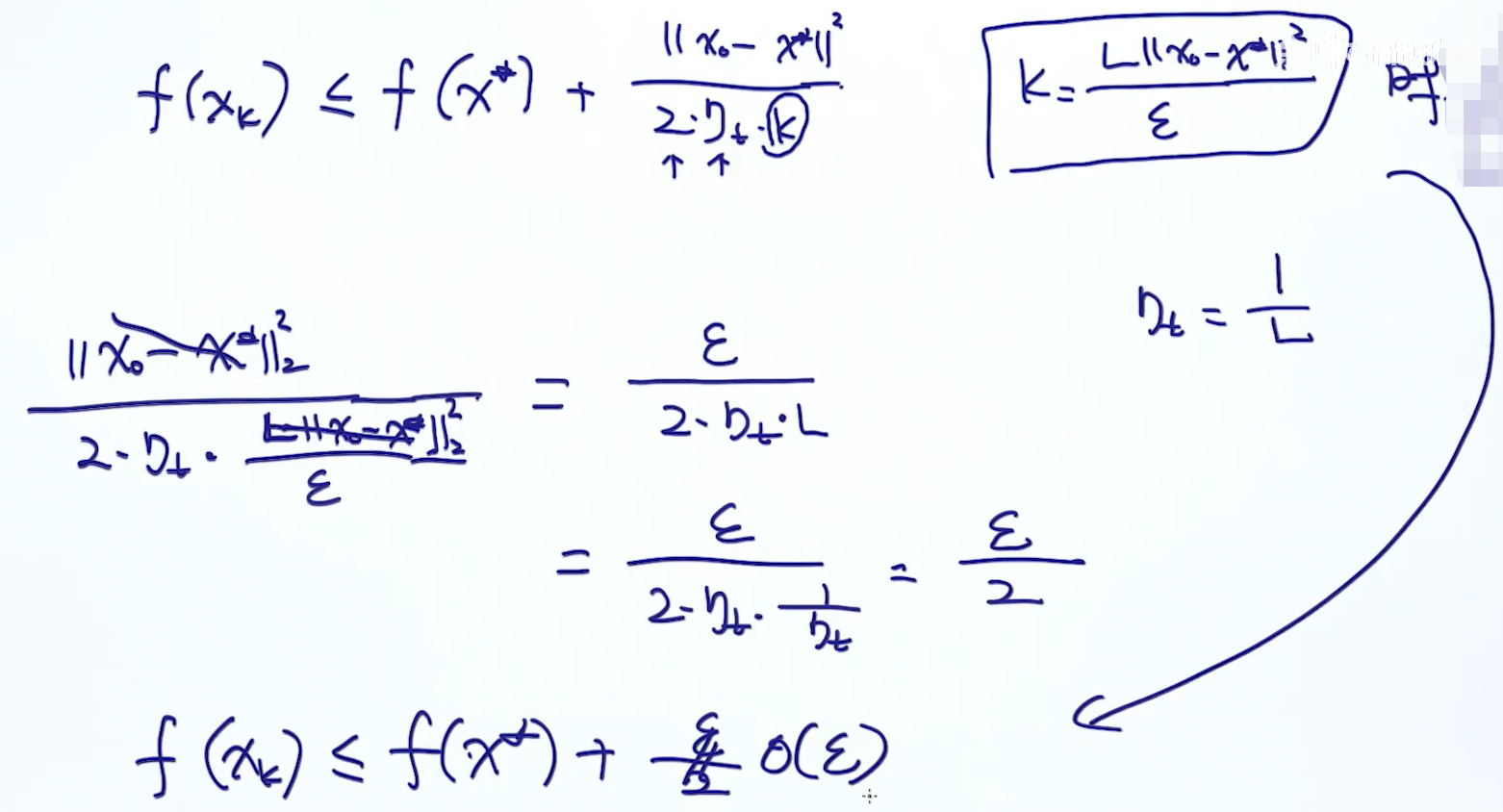
2.凸函数的性质

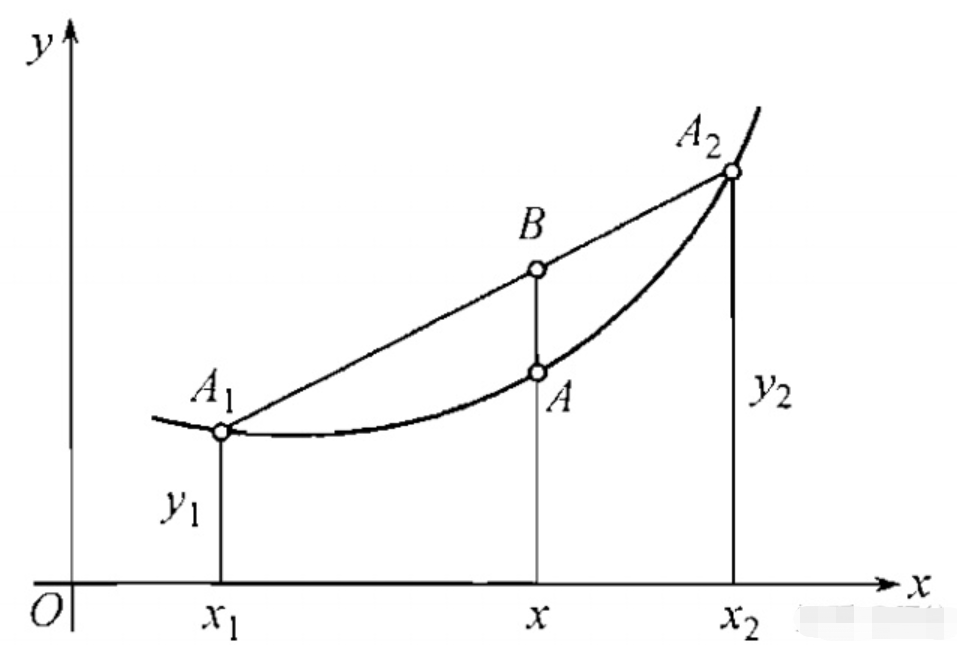




3.L-Lipschitz条件及定理
两个定理:


4.收敛性推导



上面的f(xi+1)<=f(xi)表示的是:
梯度下降法每次的更新一定要比之前的好,这是标准意义上的梯度下降法,随机梯度下降法不能保证每次的更新优于之前的。



