决策树
1.一棵决策树与对应的决策边界
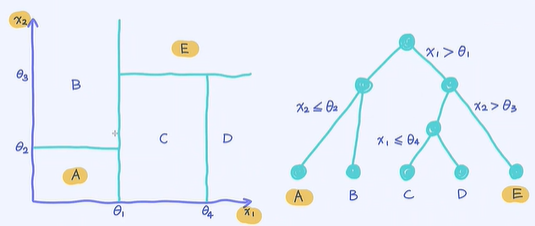
2.从数据中学习决策树
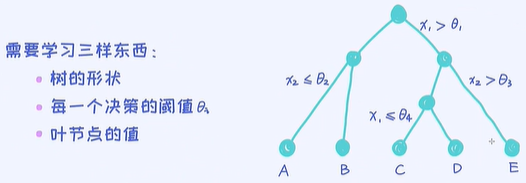
这三样东西中,树的形状是最难学出来的,因为给定一个样本数据的时候,其实树的形状有非常多个,我怎么确定哪一个形状是最优的呢?
通过贪心算法,来找出针对某一个样本数据的最好的一个决策树的形状
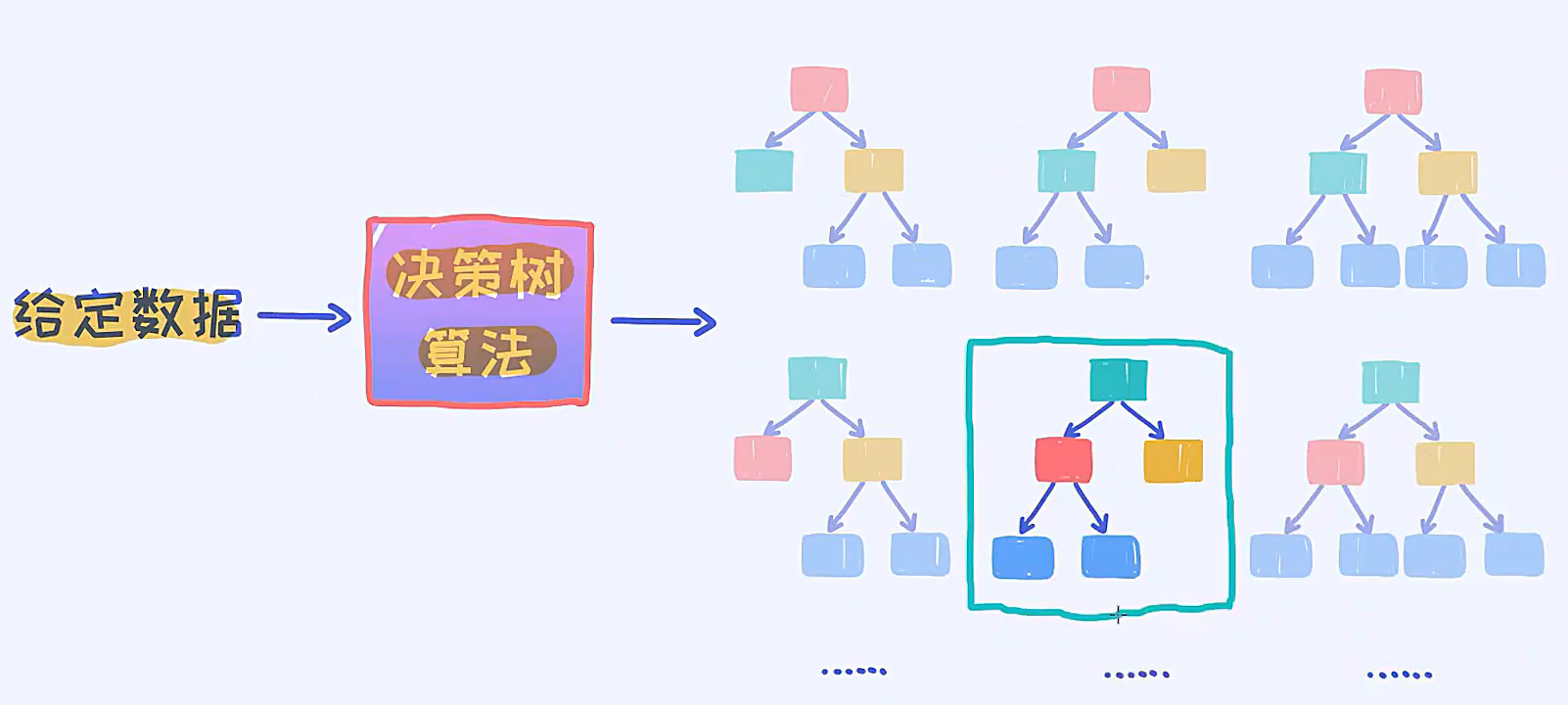
3.基于给定数据构造决策树
如何构造一棵决策树来拟合这些给定的数据
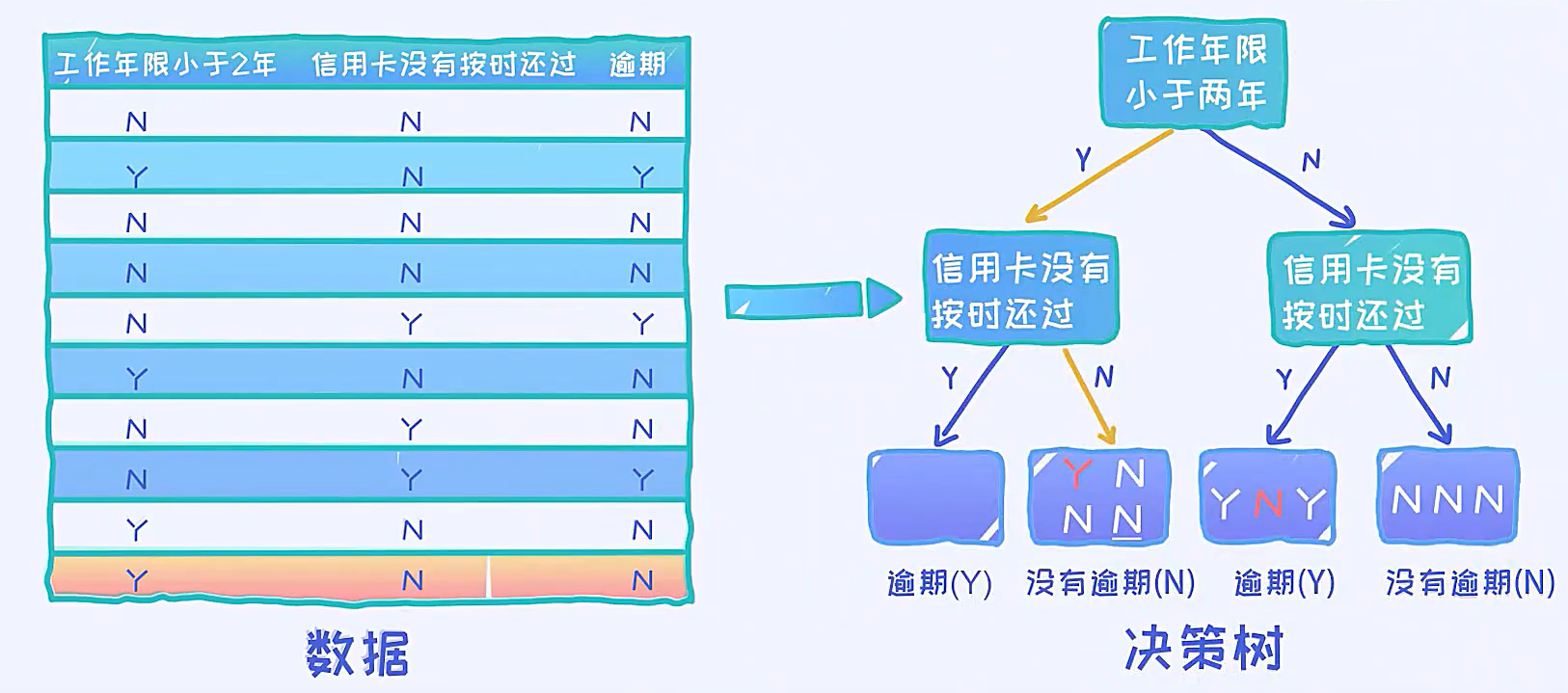
用这棵决策树去拟合这些数据,出现了2个错误,准确率80%
通常情况下,给定一批数据,我们希望找出针对这个数据最优的那棵决策树,但实际上其实最大的问题在于,如果这个数据的维度很大,相当于这里面所有可能的决策树的形状是非常庞大的。
简单来说,假如给定的数据,它的维度是D,这时候可以认为所有可能的决策树的个数是跟维度有着指数级的关系。
怎么解决这个问题,即寻找最优化的决策树?
贪心算法
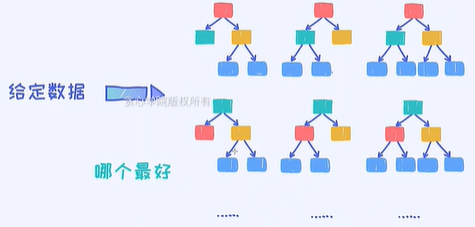
决策树算法本质就是贪心算法
3.1.好的特征有什么特点
是否头痛作为根节点的时候,决策树变得非常简单,而且只需要一个变量就可以把样本分的很清楚

好的特征可以减少不确定性
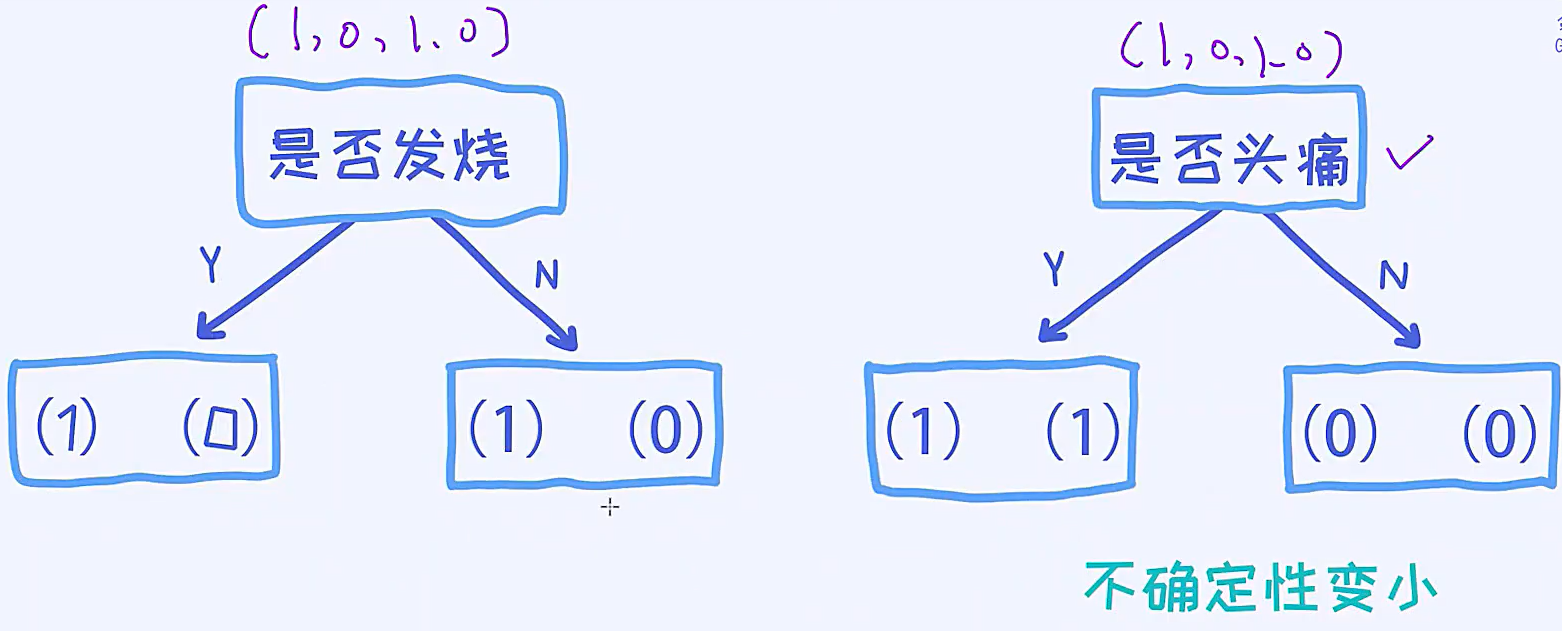
在是否发烧的决策树中,左边的叶节点里面有两个样本,分别是1,0,这个就是不确定性很高的,因为一旦有新的样本进入到这个叶节点,我还是不能区分这个新的样本到底是1还是0的;
在是否头痛的决策树中,左边的叶节点都是1,右边的叶节点都是0,当加入一个新的样本进入左边,我们知道之前的样本都是属于1的,所以这种情况下,我们可以把它认为是不确定性很低。
因此,我们想选定一个特征,选完之后,我希望带来的结果是不确定性变小。原来的四个样本都是(1,0,1,0),不确定性是一样的,但是分割完之后,不确定性完全不一样了。
根据某一个特征做分割之后,不确定性变小了,但这个怎么用数学语言来表达?
可以用信息熵计算不确定性
信息熵越大,说明不确定性越大;信息熵越小,不确定性越小
![]()
其中p表示概率

3.2 不确定性的减少怎么用数学方法表达
![]()
在构建一棵决策树的时候,应该选择什么特征,作为这棵树的根节点,这个流程在构造树的时候,会反复递归构造下去,所以每一步在构造一棵子树的时候,我都会面临一个问题,在所有的的特征中,应该选择哪个特征作为当前这棵树的根节点,这个应该怎么去确定呢?
我们可以判断每个特征对不确定性的影响,如果某个特征降低了不确定性,并且降低的不确定性最多,可以认为那个特征是最好的,因此这个特征应该出现在那棵决策树的根节点上。
原来的不确定性,就是分割之前的不确定性,这个所有的特征都是一样的
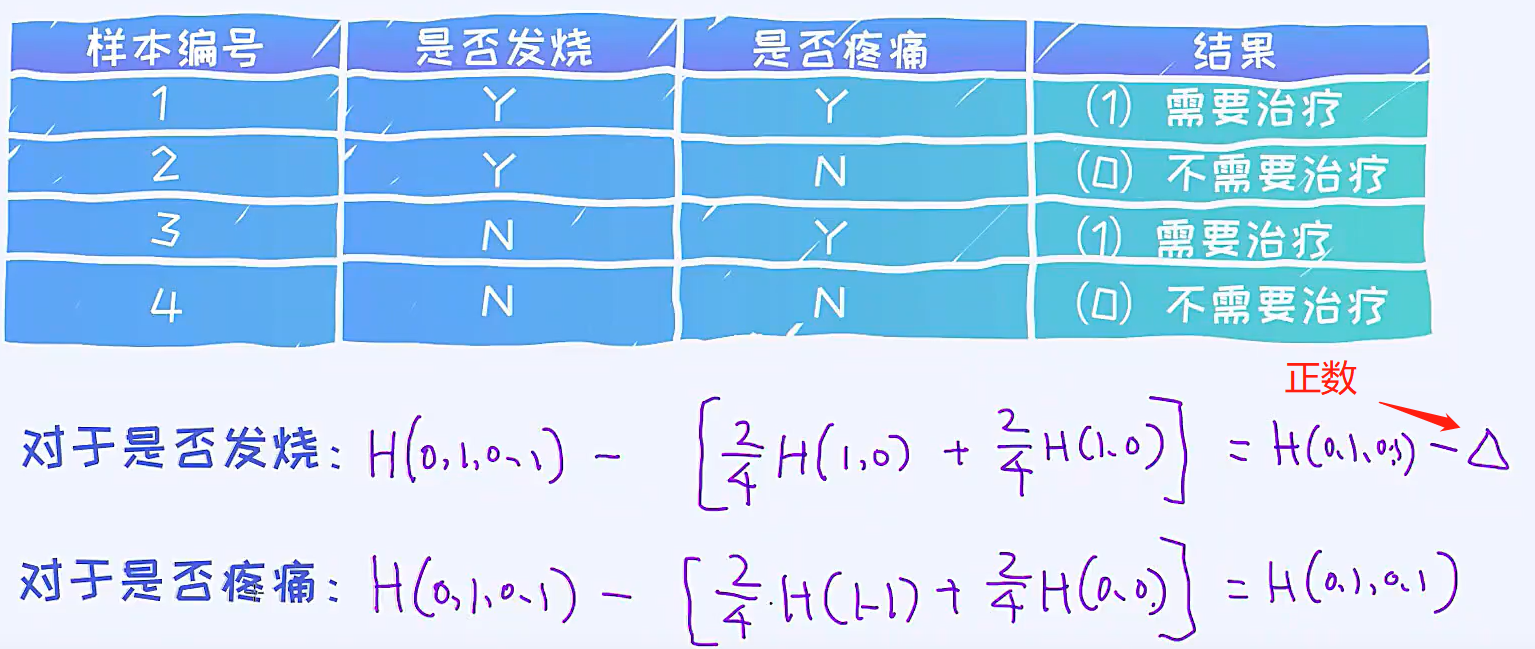
可以看到是否疼痛的熵的不确定性的减少是大于是否发烧的,因此选择是否疼痛这一特征作为当前决策树的根节点
这种不确定性的减少,叫做信息增益(Information Gain),因此信息增益=原始的信息熵-分割后的信息熵
3.3 构建决策树
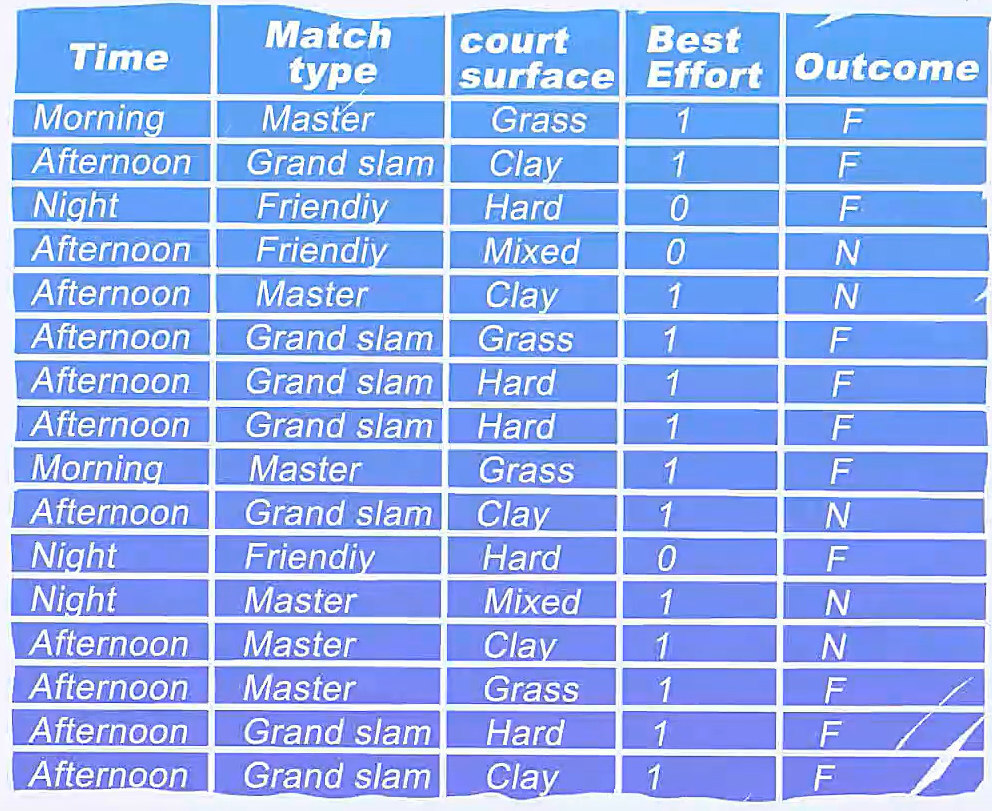
对于Time这一个特征,有三个变量,根据变量,我们把样本分到三个叶节点中


我们把每个特征的信息增益算出来,哪个特征的信息增益是最大的,就选择那个特征作为当前的根节点就可以了。
发现Court Surface是最好的特征
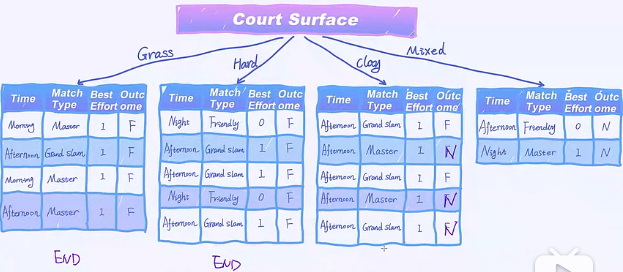
这里面唯一需要持续做分裂的是clay这个分支
4.决策树过拟合
(1)决策树性能与节点个数之间的关系
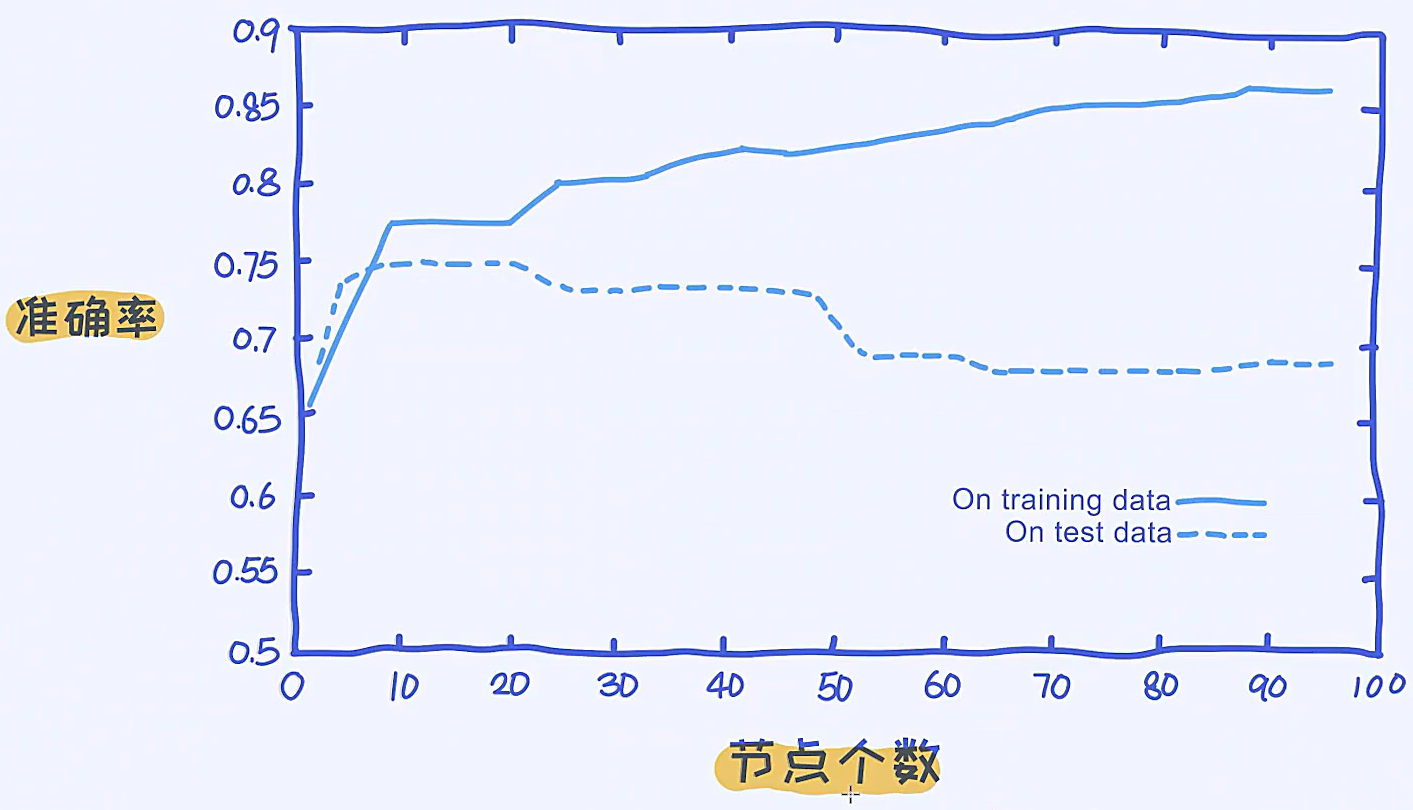
可以看到当节点个数越来越多的时候,在训练数据上的准确率是不断上升的,在测试数据上,一开始准确率上升,后面会慢慢下降,这是过拟合现象,所以在调参的时候,节点的个数是一个很重要的参数。
节点的个数也可以表现在一棵树的深度,或是一个叶节点包含多少个样本上,所以叶节点假设它包含很多的样本,那么很显然,节点的个数是变小的。
因此节点的个数与模型的过拟合是有紧密相关的关系。
(2)如何避免决策树的过拟合(如何去减少决策树的节点的个数?)
- 设置树的最大深度(maximum depth)
- 当叶节点里的样本个数少于阈值时停止分裂
- 具体阈值选择多少取决于交叉验证的结果
最大深度和阈值就是决策树模型的超参数,超参数可以通过交叉验证确定
5.如何处理连续性(real-valued)特征
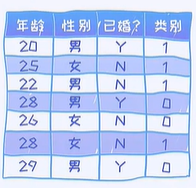
年龄是连续性的特征,可以穷举的
连续性特征,可以有无穷多个分割点,如何选择合理的分割点?
将一个连续型变量映射到二分类的变量里面

连续型变量与类别型变量(性别,已婚?)的最大区别在于,针对连续型变量,我们可以从一个特征里面提取很多不一样的规则出来,如年龄>=20,年龄<20;年龄>=22,年龄<22;
然后把每个规则都要去计算一下信息增益,再从这里面选出其中最好的,再跟其他的类别型变量做比较。
6.回归决策树
分类时候使用信息熵,回归时候使用标准差
分裂前的标准差

候选分裂特征:天气情况

候选分裂特征:温度

候选分裂特征:湿度

候选分裂特征:是否有风

第一次分裂之后

运动时间是连续型的,针对这种回归问题,用决策树,就要使用标准差
7.决策树的loss
决策树生长的核心在于如何选择最优特征作为当前结点分割的特征。
当决策树如此生长完成后,对训练集程度会很好,但是对测试集一般都会出现高方差、过拟合的现象,如何预防这种现象,就是之前提到的预剪枝、后剪枝方法。
而剪枝过程换个方法来讲,其实就是在优化降低Loss function的的过程。

其中,经验熵为:
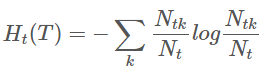
右边第一项表示误差大小,第二项表示模型的复杂度,也就是用叶节点表示,防止过拟合。
损失函数中的第一项表示模型对训练数据的预测误差,也就是模型的拟合程度,第二项表示模型的复杂程度,通过参数 α 控制二者的影响力。一旦 α 确定,那么我们只要选择损失函数最小的模型即可。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号