损失函数
1.损失函数

(1)均方误差

例子:
#! /usr/bin/env python
# -*- coding:utf-8 -*-
# __author__ = "yanjungan"
import tensorflow as tf
import numpy as np
SEED = 23455
rdm = np.random.RandomState(seed=SEED) # 生成(0, 1)之间的随机数
# 生成32行2列(0, 1)
x = rdm.rand(32, 2)
# 生成噪声[0,1)/10=[0,0.1); [0,0.1)-0.05=[-0.05,0.05)
y_ = [[x1 + x2 + (rdm.rand() / 10.0 - 0.05)] for (x1, x2) in x]
# 强制转换x的数据类型
x = tf.cast(x, dtype=tf.float32)
w1 = tf.Variable(tf.random.normal([2, 1], stddev=1, seed=1))
epoch = 15000
lr = 0.002
for epoch in range(15000):
with tf.GradientTape() as tape:
y = tf.matmul(x, w1)
loss_mse = tf.reduce_mean(tf.square(y_ - y))
# 生成导数,梯度
grads = tape.gradient(loss_mse, w1)
# 更新w1, w1 = w1-lr*grads
w1.assign_sub(lr*grads)
if epoch % 500 == 0:
print('After %d training steps, w1 is '% (epoch))
print(w1.numpy(), "\n")
print("Final w1 is:", w1.numpy())
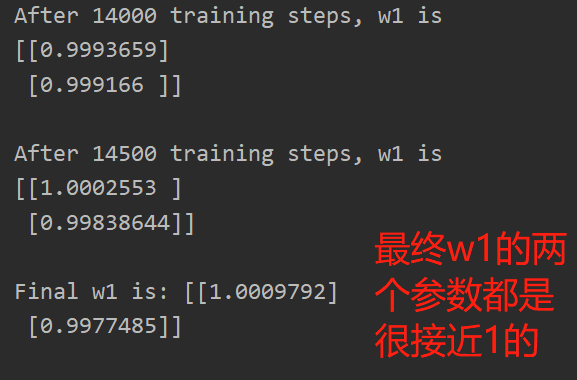
最终w1的两个参数都是很接近1的,即,y=1.00*x1+1.00*x2,这一结果和我们制造数据集的公式y=1*x1+1*x2一致,说明预测酸奶的日销量拟合公式正确
(2)交叉熵损失函数

通过交叉熵的值,可以判断哪个预测的值(y)与实际值(y_)更接近,交叉熵越小,预测越准
2.softmax与交叉熵结合
我们在执行分类问题时,通常先用softmax函数让输出结果符合概率分布,再求交叉熵损失函数
tensorflow给出了可同时计算概率和交叉熵的函数

即输出先过softmax函数,再计算y与y_的交叉熵损失函数
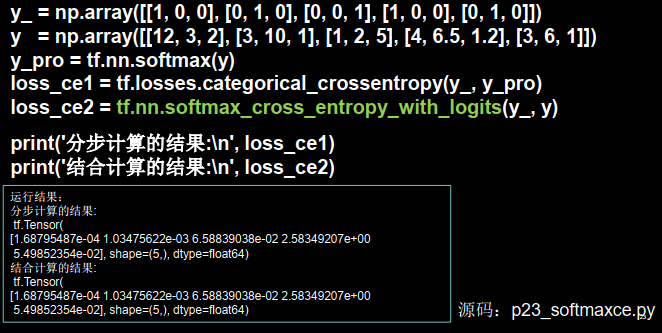
2.神经网络的分类模型的loss为什么用交叉熵
分类问题,都用onehot+cross entropy
在训练的过程中,分类问题用cross entropy;回归问题用mean squared error
训练之后,validation/testing时,使用classification error,更直观,而且是我们最关注的指标。
交叉熵描述更合理,能更好的贴近原标签的分布情况,而不是单纯的0,1误差进行计算,而且容易收敛,不会有很多局部极值点。用于分类问题,输出是一个概率分布,通过交叉熵更能反映分布的接近
下面是解释:
监督学习的 2 大分支:
- 分类问题:目标变量是离散的。
- 回归问题:目标变量是连续的数值。
本文讨论的是分类模型。
例如:根据年龄、性别、年收入等相互独立的特征, 预测一个人的政治倾向(民主党、共和党、其他党派)。
为了训练模型,必须先定义衡量模型好与坏的标准。
在机器学习中,我们使用 loss / cost,即, 当前模型与理想模型的差距。
训练的目的,就是不断缩小 loss / cost。
(1)为什么不能用classification error
大多数人望文生义的 loss,可能是这个公式
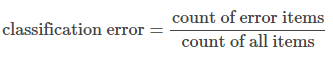
我们用一个的实际模型来看 classification error 的弊端。
使用 3 组训练数据。
computed 一栏是预测结果,targets 是预期结果(真实值)。 二者的数字,都可以理解为概率。 correct 一栏表示预测是否正确。

item 1 和 2 以非常微弱的优势判断正确,item 3 则彻底错误

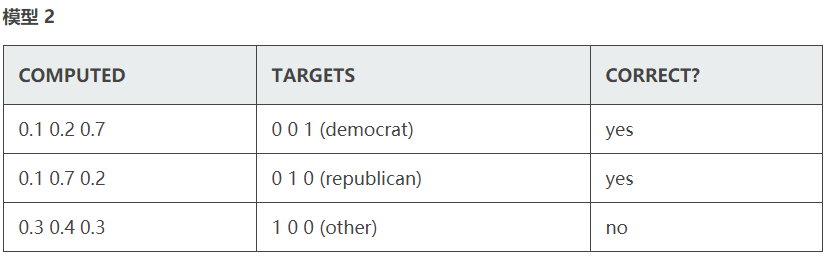
tem 1 和 2 的判断非常精准,item 3 判错,但比较轻

结论
2 个模型的 classification error 相等,但模型 2 要明显优于模型 1
classification error 很难精确描述模型与理想模型之间的距离
(2)cross-entropy的效果对比
如果使用 ACE ( average cross-entropy error )
TensoFlow 官网的 MNIST For ML Beginners 中 cross entropy 的计算公式是:
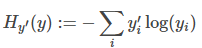
其中,yi'是真实值,yi是预测值
根据公式, 第一个模型中第一项的 cross-entropy 是:
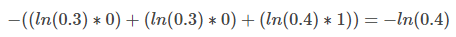
所以,第一个模型的 ACE ( average cross-entropy error ) 是
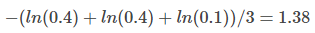
第二个模型的 ACE 是:
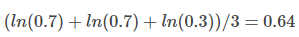
结论
ACE 结果准确的体现了模型 2 优于模型 1。
cross-entropy 更清晰的描述了模型与理想模型的距离。
(3)为什么不用Mean Squared Error(平方和)
若使用 MSE(mean squared error)
第一个模型第一项的 loss 是
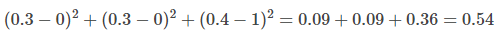
第一个模型的 loss 是

第二个模型的 loss 是
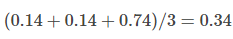
MSE 看起来也是蛮不错的。为何不用?
分类问题,最后必须是 one hot 形式算出各 label 的概率, 然后通过 argmax 选出最终的分类。 (稍后用一篇文章解释必须 one hot 的原因)
在计算各个 label 概率的时候,用的是 softmax 函数。
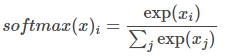
如果用 MSE 计算 loss, 输出的曲线是波动的,有很多局部的极值点。 即,非凸优化问题 (non-convex)
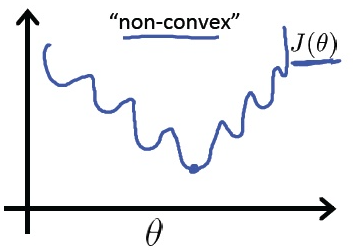
cross entropy 计算 loss,则依旧是一个凸优化问题,

用梯度下降求解时,凸优化问题有很好的收敛特性。
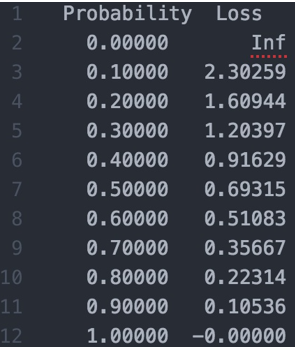
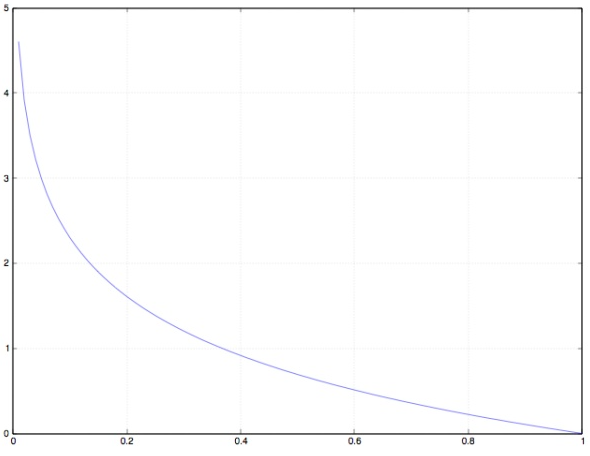
最后,定量的理解一下 cross entropy。 loss 为 0.1 是什么概念,0.01 呢?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号