神经网络的复杂度&指数衰减学习率&激活函数
1.神经网络复杂度（空间复杂度+时间复杂度）
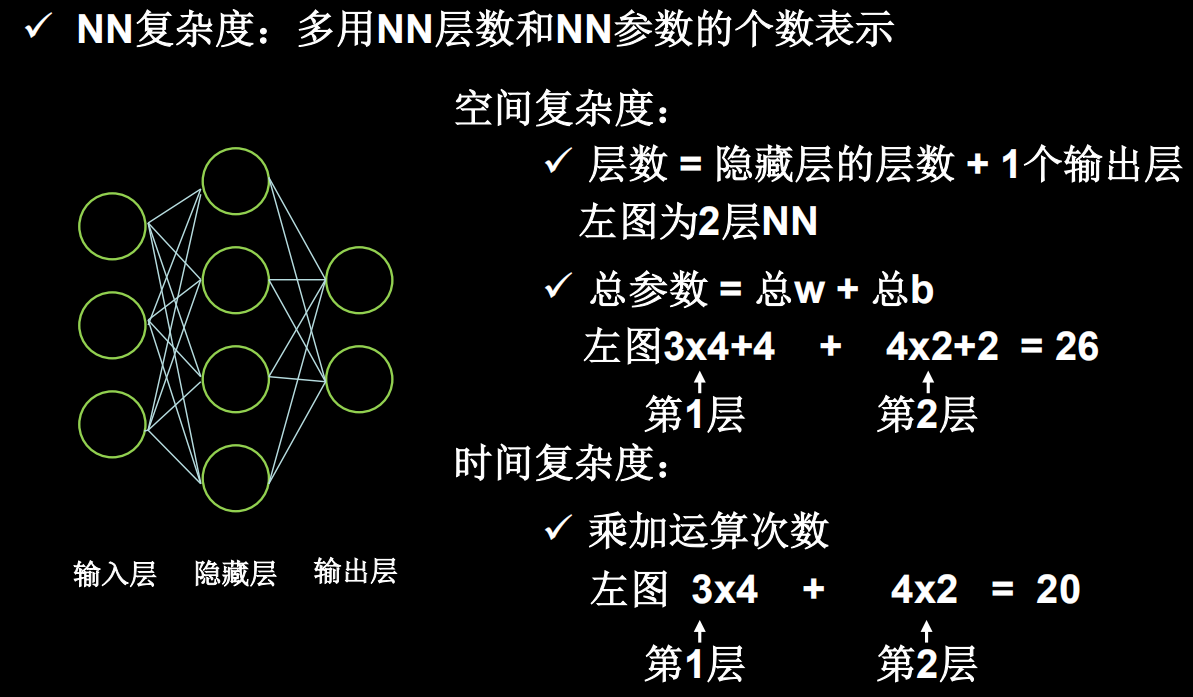
- 空间复杂度
空间复杂度用神经网络层数和神经网络中待优化参数的个数表示
我们计算神经网络层数时，只统计具有运算能力的层，输入层仅把数据传输过来，没有运算，所以在统计神经网络层数时，不把输入层算进来
输入层和输出层之间都是隐藏层
- 时间复杂度
时间复杂度可以用神经网络中的乘加运算的次数表示
有几条权重线，就有几次乘加运算
2.学习率
指数衰减学习率可以根据当前迭代次数，动态改变学习率的值
当前轮数有两种表示方法：
- epoch可以用当前迭代了多少次数据集
- global_step表示当前一共迭代了多少次batch
多少轮衰减一次：
迭代多少次数据集，或迭代多少次batch更新一次学习率，决定了学习率的更新频率
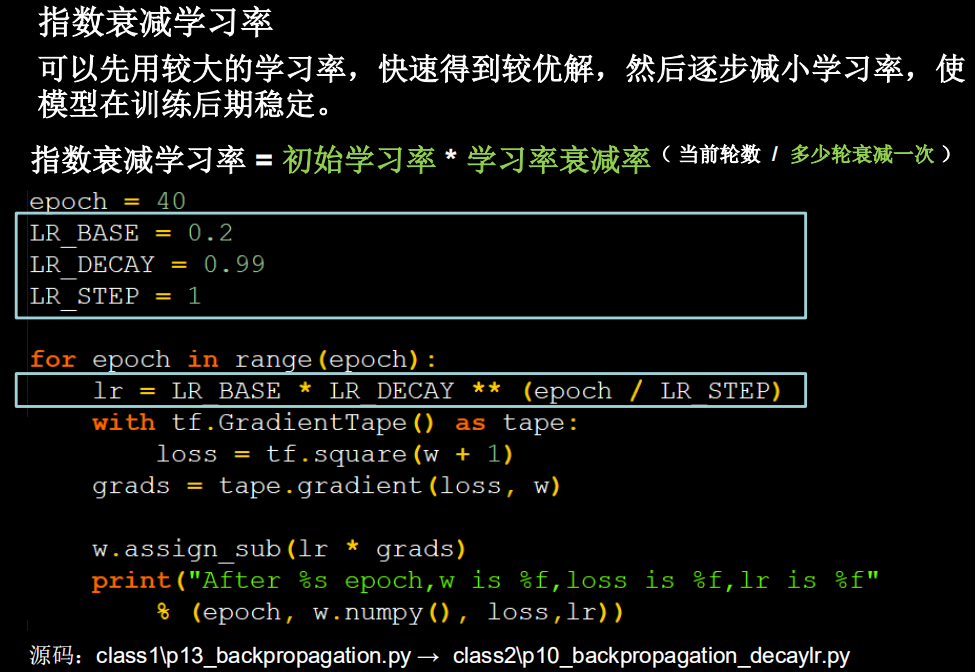
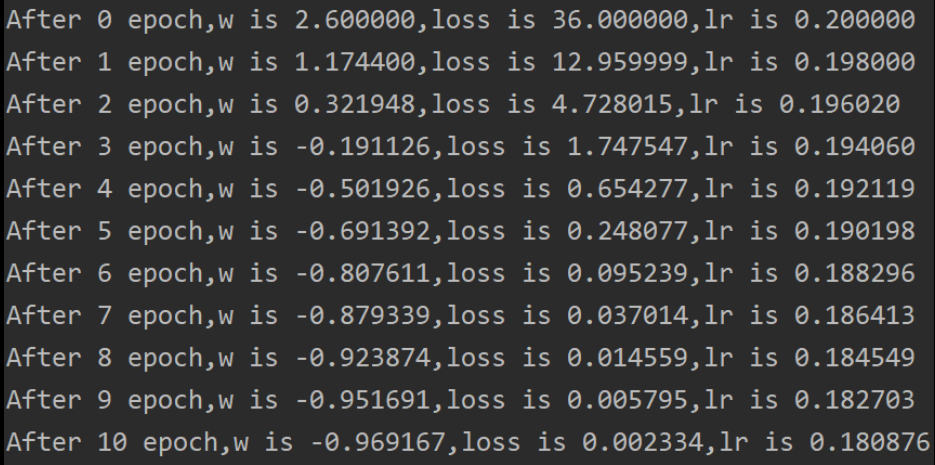
代码运行输出：
可以看到随着迭代轮数增加，学习率在指数衰减
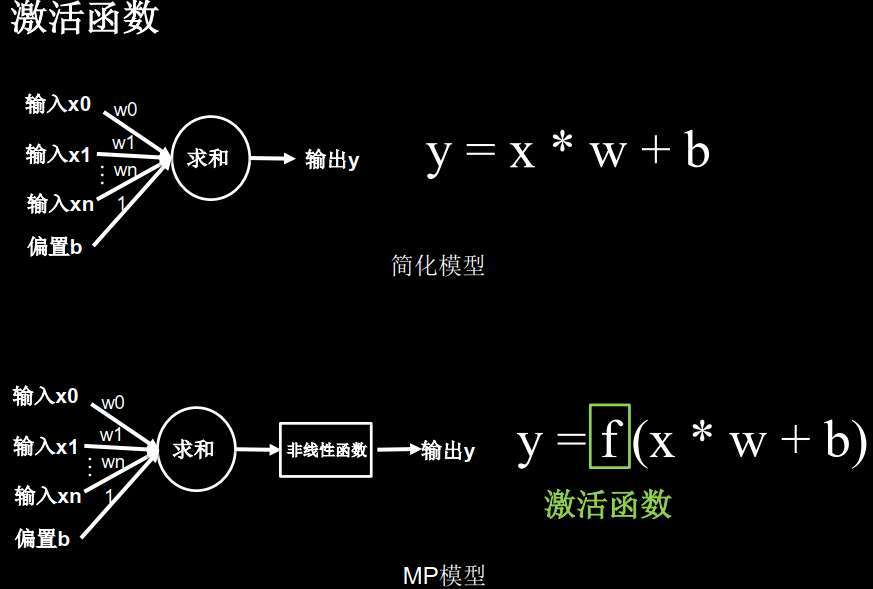
3.激活函数
激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。引入非线性激活函数，可使深层神经网络的表达能力更加强大
也正是非线性函数的加入，使得多层神经网络不再是输入x的线性组合，神经网络可以随层数的增加提升表达力了
举例说明：
神经元后面，要跟个激活层，从而引入非线性因素，这就像人的神经元一样，让细胞处于兴奋或抑制的状态。
数学模拟的形式就是通过激活函数，大于阈值就激活，反之抑制。
如果激活函数的输出为有限值，权重对特征的影响更显著，用梯度下降的方法更新参数会更稳定
如果激活函数的输出为无限值，参数的初始值对模型的影响非常大，要使用更小的学习率
优点：
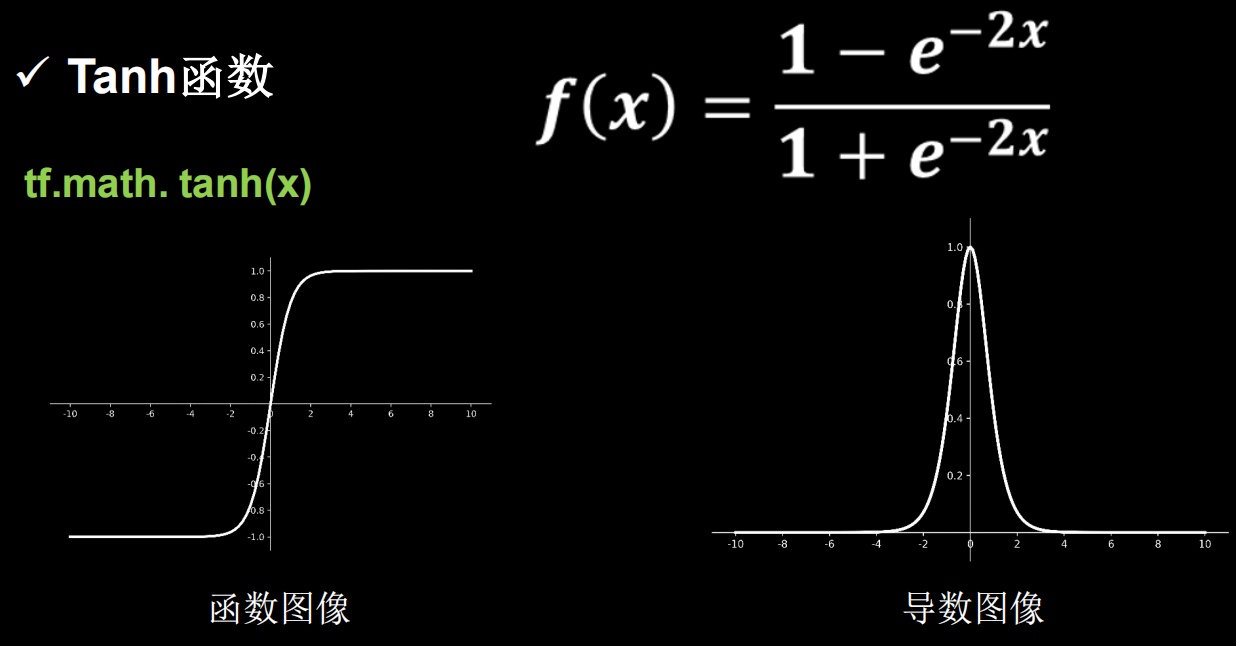
- 输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可用作输出层；
- 求导容易。
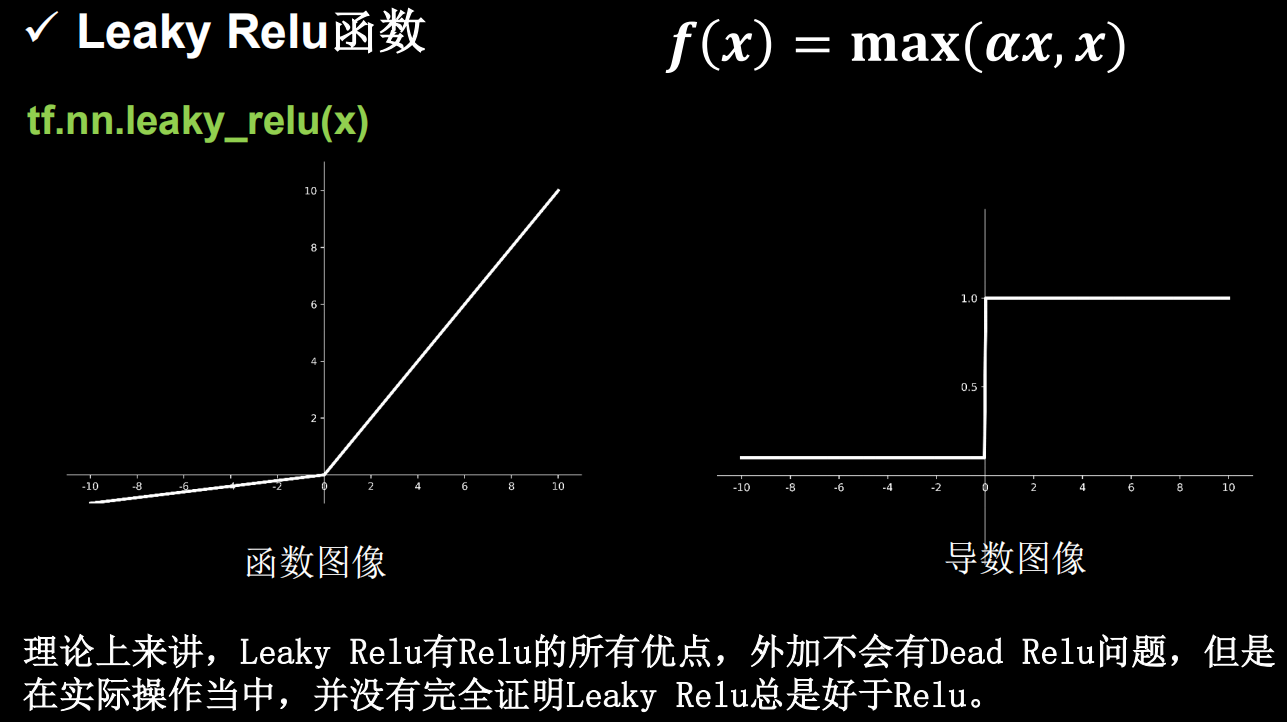
解释Dead Relu问题
送入激活函数的输入特征是负数时，激活函数的输出为0，反向传播得到的梯度是0，导致参数无法更新，造成神经元死亡。
其实造成神经元死亡的根本原因是经过relu函数的负数特征过多导致的，我们可以改进随机初始化，避免过多的负数特征送入relu函数，可以通过设置更小的学习率，减少参数分布的巨大变化，避免训练中产生过多的负数特征进入relu函数。
