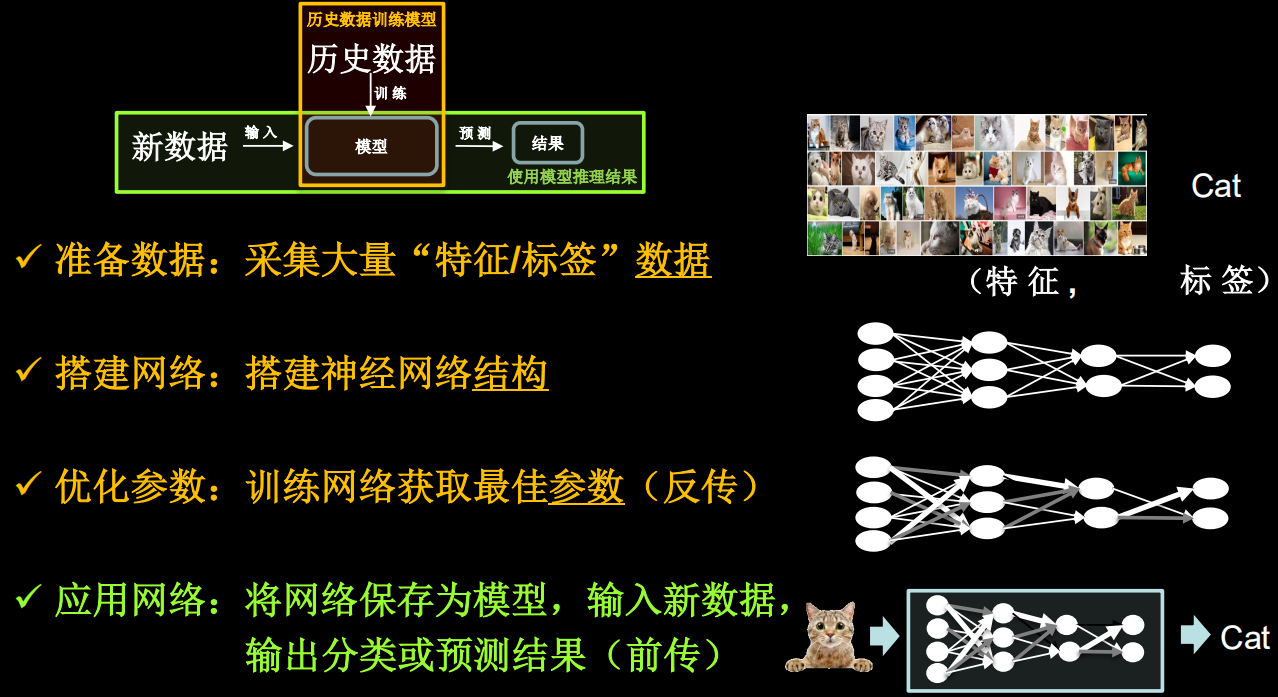
神经网络设计过程
1.背景：
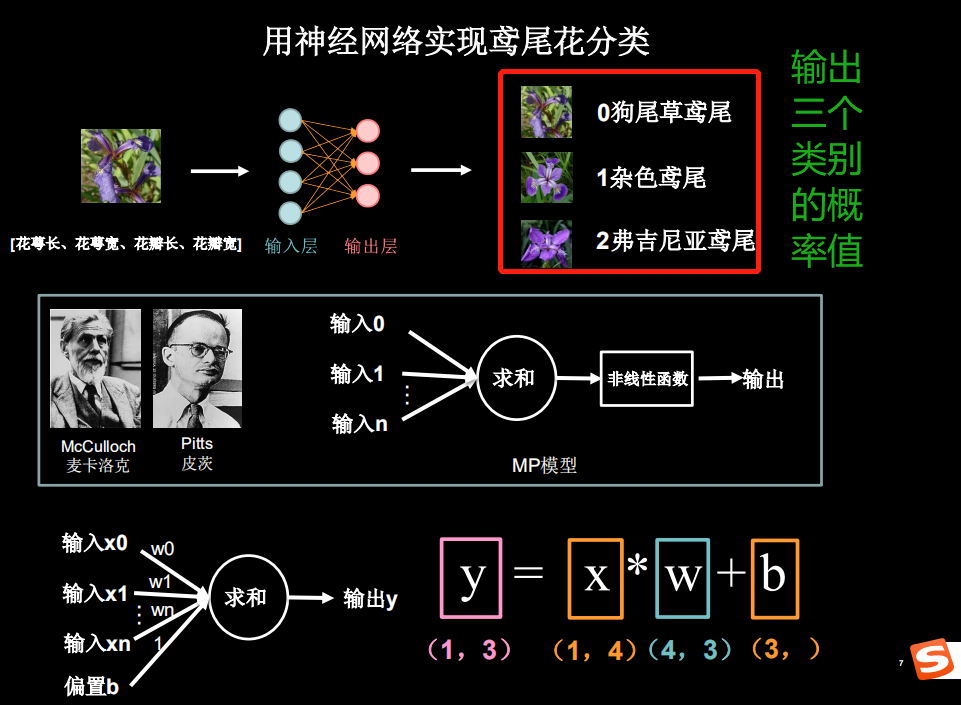
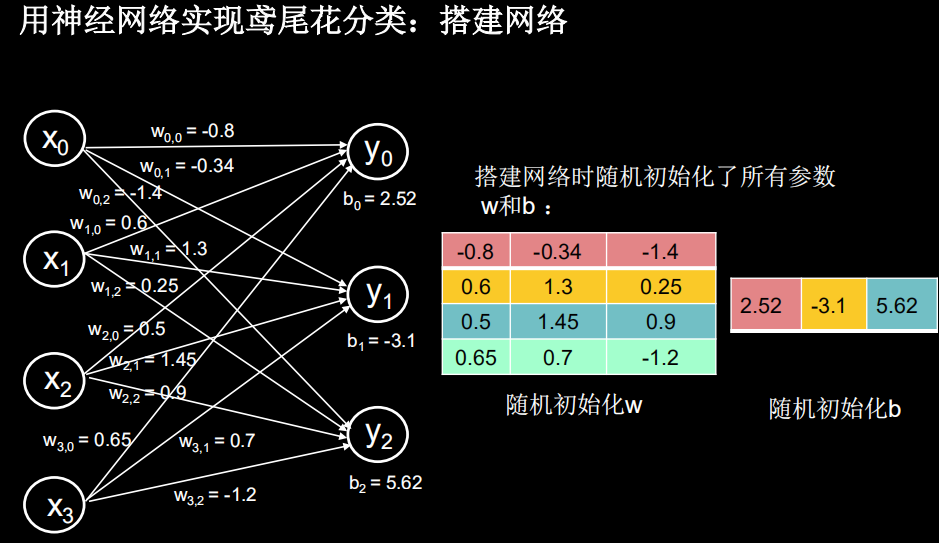
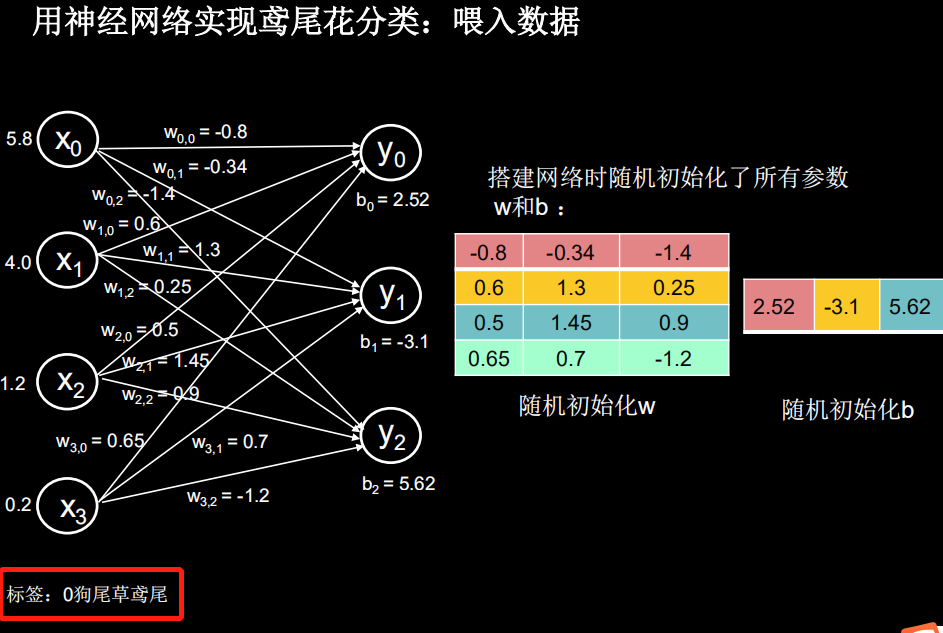
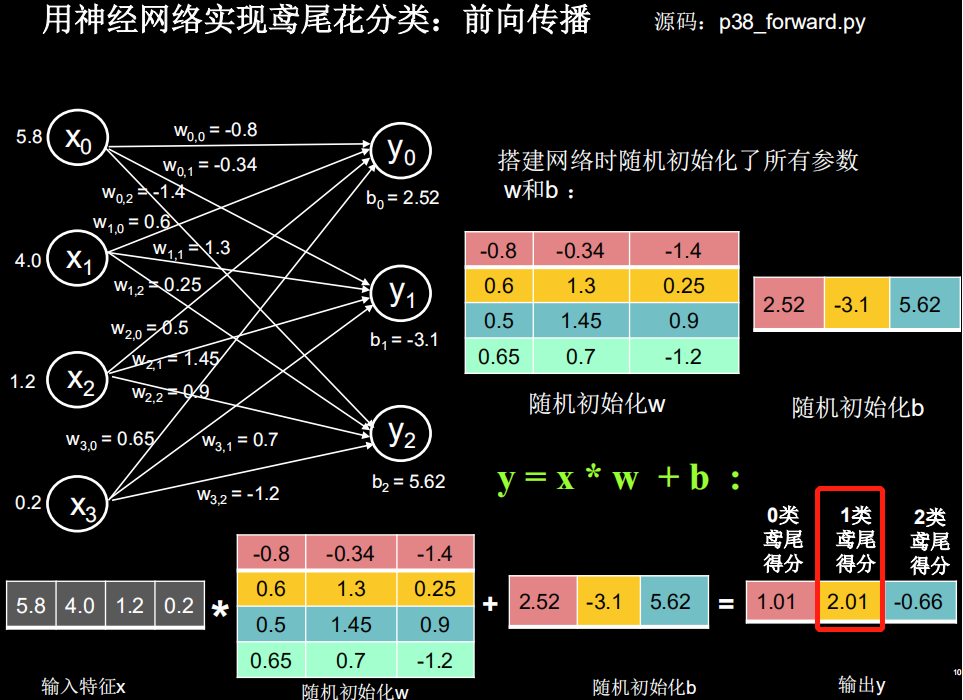
输出 y 中，1.01 代表 0 类鸢尾得分，2.01 代表 1 类鸢尾得分，-0.66 代表 2 类鸢尾得分。通过输出 y 可以看出数值最大(可能性最高)的是 1 类鸢尾，而不是标签 0 类鸢尾。这是由于最初的参数 w 和b 是随机产生的，现在输出的结果是蒙的
为了修正这一结果，我们用损失函数，定义预测值 y 和标准答案(标签) y_ 的差距，损失函数可以定量的判断当前这组参数 w 和b 的优劣，当损失函数最小时，即可得到最优 w 的值和b 的值。
损失函数的定义有多种方法，均方误差就是一种常用的损失函数，它计算每个前向传播输出 y 和标准答案 y_ 的差求平方再求和再除以 n 求平均值，表征了网络前向传播推理结果和标准答案之间的差距。
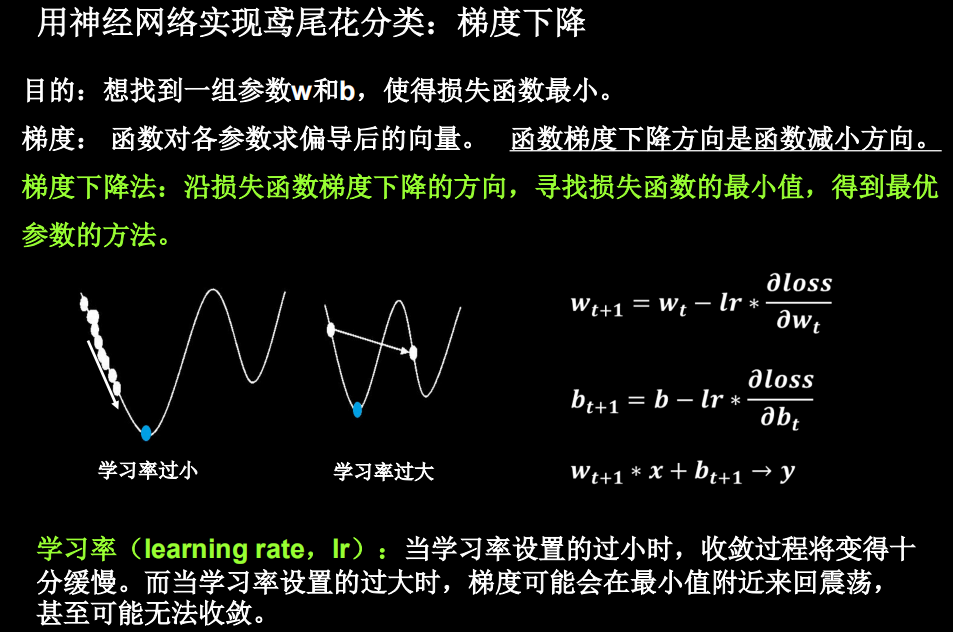
通过上述对损失函数的介绍，其目的是寻找一组参数 w 和b 使得损失函数最小。为达成这一目的，我们采用梯度下降的方法。损失函数的梯度表示损失函数对各参数求偏导后的向量，损失函数梯度下降的方向，就是是损失函数减小的方向。梯度下降法即沿着损失函数梯度下降的方向，寻找损失函数的最小值，从而得到最优的参数。梯度下降法涉及的公式如下
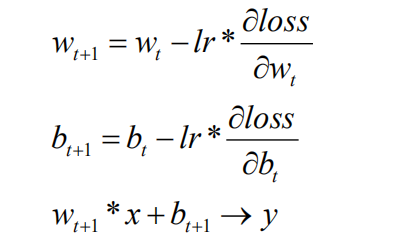
上式中，lr 表示学习率，是一个超参数，表征梯度下降的速度。如学习率设置过小，参数更新会很慢，如果学习率设置过大，参数更新可能会跳过最小值。
上述梯度下降更新的过程为反向传播，下面通过例子感受反向传播。利用如下公式对参数 w 进行更新。
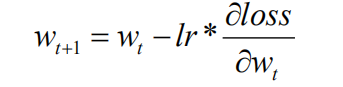
设损失函数为 (w+1)2 ，则其对 w 的偏导数为 2w+ 2 。设 w 在初始化时被随机初始化为 5，学习率设置为 0.2。则我们可按上述公式对 w 进行更新：
第一次参数为 5，按上式计算即5 − 0.2×(2×5 + 2) =2.6。
同理第二次计算得到参数为 1.16，第三次计算得到参数为 0.296……
画出损失函数 2 (w+1) 的图像，可知 w = −1时损失函数最小，我们反向传播
优化参数的目的即为找到这个使损失函数最小的 w = −1值
