BFS(找最短距离,最短路径)二叉树最小深度&打开转盘锁&对称二叉树
BFS 的核心思想应该不难理解的,就是把一些问题抽象成图,从一个点开始,向四周开始扩散。一般来说,我们写 BFS 算法都是用「队列」这种数据结构,每次将一个节点周围的所有节点加入队列。
BFS 相对 DFS 的最主要的区别是:BFS 找到的路径一定是最短的,但代价就是空间复杂度比 DFS 大很多
问题的本质就是让你在一幅「图」中找到从起点start到终点target的最近距离,这个例子听起来很枯燥,但是 BFS 算法问题其实都是在干这个事儿。
最短路径问题用BFS实现
分析思路:
首先明确下起点start和终点target是什么,怎么判断到达了终点?
显然起点就是root根节点,终点就是最靠近根节点的那个叶子节点,叶子节点就是两个子节点都是null的节点
if not tmp.left and not tmp.right:
// 到达终点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def minDepth(self, root: TreeNode) -> int:
if not root:
return 0
q = [root]
count = 1 # root 本身就是一层,count初始化为 1(count是深度)
while q:
for i in range(len(q)): # 遍历当前层的所有节点
tmp = q.pop(0)
if not tmp.left and not tmp.right: # 判断是否到达终点,发现叶子节点,返回当前层数(深度)
return count
# 队列中不放空节点
if tmp.left:
q.append(tmp.left)
if tmp.right:
q.append(tmp.right)
# 进入下一层,深度加1
count += 1
return count
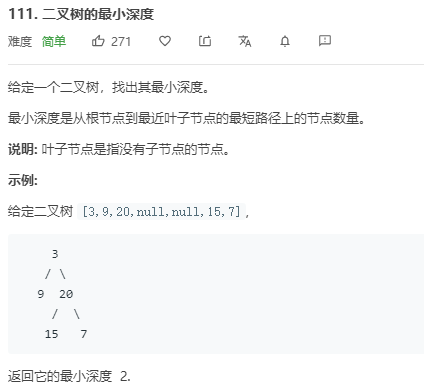
q = [root]打印出来的结果:
[TreeNode{val: 3, left: TreeNode{val: 9, left: None, right: None}, right: TreeNode{val: 20, left: TreeNode{val: 15, left: None, right: None}, right: TreeNode{val: 7, left: None, right: None}}}]
q初始的值
1、为什么 BFS 可以找到最短距离,DFS 不行吗?
首先,你看 BFS 的逻辑,depth每增加一次,队列中的所有节点都向前迈一步,这保证了第一次到达终点的时候,走的步数是最少的。
DFS 不能找最短路径吗?其实也是可以的,但是时间复杂度相对高很多。
你想啊,DFS 实际上是靠递归的堆栈记录走过的路径,你要找到最短路径,肯定得把二叉树中所有树杈都探索完才能对比出最短的路径有多长对不对?
而 BFS 借助队列做到一次一步「齐头并进」,是可以在不遍历完整棵树的条件下找到最短距离的。
形象点说,DFS 是线,BFS 是面;DFS 是单打独斗,BFS 是集体行动。这个应该比较容易理解吧。
2、既然 BFS 那么好,为啥 DFS 还要存在?
BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复杂度较低。
还是拿刚才我们处理二叉树问题的例子,假设给你的这个二叉树是满二叉树,节点总数为N,对于 DFS 算法来说,空间复杂度无非就是递归堆栈,最坏情况下顶多就是树的高度,也就是O(logN)。
但是你想想 BFS 算法,队列中每次都会储存着二叉树一层的节点,这样的话最坏情况下空间复杂度应该是树的最底层节点的数量,也就是N/2,用 Big O 表示的话也就是O(N)。
由此观之,BFS 还是有代价的,一般来说在找最短路径的时候使用 BFS,其他时候还是 DFS 使用得多一些(主要是递归代码好写)。
思路:用BFS解决这道题目,关键在于将题目转变成BFS的解题模式
BFS一般步骤:先确定一个搜索范围、起始点、标记和目标,然后写出相邻关系函数。先将起始点出列,马上与它相邻点入列,并标记为已访问,如此循环,直到列表为空。这样就能一直搜索,直到找到目标点。
题目特征:
搜索范围:0000至9999这一千个节点
起始节点:0000
相邻关系:4个位置每次只有一个能+1或者-1(0-1则为9)
目标节点:target
额外条件:节点不会在deadends中
class Solution:
def openLock(self, deadends: List[str], target: str) -> int:
# 生成器
def neighbors(node):
for i in range(0, 4):
x = int(node[i])
for d in (-1, 1):
y = (x+d) % 10
yield node[:i] + str(y) + node[i+1:]
import collections
queue = collections.deque([('0000', 0)])
dead = set(deadends)
seen = {'0000'} # 集合
while queue:
node, depth = queue.popleft()
if node == target:
return depth
if node in dead:
continue
else:
# neighbors(node) 生成器对象
for nei in neighbors(node):
if nei not in seen:
seen.add(nei)
queue.append((nei, depth+1))
return -1


# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
import collections
queue = collections.deque()
queue.append((root, root))
while queue:
left, right = queue.popleft()
if not left and not right:
continue
if not left or not right:
return False
if left.val != right.val:
return False
queue.append((left.left, right.right))
queue.append((left.right, right.left))
return True


 浙公网安备 33010602011771号
浙公网安备 33010602011771号