最大子序和（动态规划）

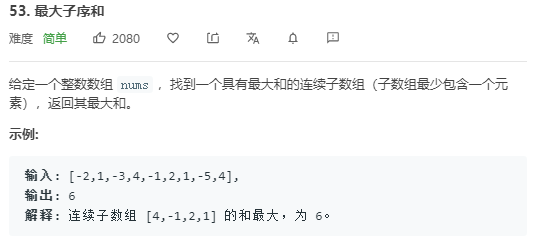
其实第一次看到这道题，我首先想到的是滑动窗口算法，因为我们前文说过嘛，滑动窗口算法就是专门处理子串/子数组问题的，这里不就是子数组问题么？
但是，稍加分析就发现，这道题还不能用滑动窗口算法，因为数组中的数字可以是负数。
滑动窗口算法无非就是双指针形成的窗口扫描整个数组/子串，但关键是，你得清楚地知道什么时候应该移动右侧指针来扩大窗口，什么时候移动左侧指针来减小窗口。
而对于这道题目，你想想，当窗口扩大的时候可能遇到负数，窗口中的值也就可能增加也可能减少，这种情况下不知道什么时机去收缩左侧窗口，也就无法求出「最大子数组和」。

解法一：动态规划思想

最重要的是理解dp数组所存储元素的含义：

明确 dp[i] 存储的不是从 0 到 i 这个范围内所得到的最大的连续子数组的和，而是以 nums[i] 为结尾的子数组所能达到的最大的和。

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        if len(nums) == 0:
            return 0
        if len(nums) == 1:
            return nums[0]
            
        # 下面是长度至少为2的情况
        dp = nums[:]  # 初始化dp数组，dp[i]存储的是以nums[i]结尾的子数组和的最大值
        for i in range(1, len(nums)):
            dp[i] = max(dp[i], dp[i-1] + dp[i])  # 更新dp[i]
        
        res = dp[0]
        for i in range(1, len(nums)):
            res = max(res, dp[i])  # 更新全局最大值
        return res

 

解法二：暴力解法

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        sum = 0
        tmp = nums[0]
        for i in range(len(nums)):
            if sum < 0:
                sum = nums[i]

            else:
                sum += nums[i]

            tmp = max(sum, tmp)

        return tmp