MATLAB解含参数方程、矩阵方程、二阶微分方程组
1、如下公式: 其中x、y、m、n为参数,a、b为未知数,利用MATLAB求解方程;
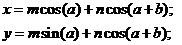
syms x y m n a b;
[a,b]=solve('x=m*cos(a)+n*cos(a+b)','y=m*sin(a)+n*sin(a+b)','a','b');
会得到四组解;对a(3)、b(3)、a(4)、b(4)进行化简,
simplify(a(3));
simplify(b(3));
simplify(a(4));
simplify(a(4));
得到:
a(3)= 2*atan((2*m*y - (- m^4 + 2*m^2*n^2 + 2*m^2*x^2 + 2*m^2*y^2 - n^4 + 2*n^2*x^2 + 2*n^2*y^2 - x^4 - 2*x^2*y^2 - y^4)^(1/2))/(m^2 + 2*m*x - n^2 + x^2 + y^2));
b(3)= 2*atan(((- m^2 + 2*m*n - n^2 + x^2 + y^2)*(m^2 + 2*m*n + n^2 - x^2 - y^2))^(1/2)/(- m^2 + 2*m*n - n^2 + x^2 + y^2));
a(4)= 2*atan((2*m*y + (- m^4 + 2*m^2*n^2 + 2*m^2*x^2 + 2*m^2*y^2 - n^4 + 2*n^2*x^2 + 2*n^2*y^2 - x^4 - 2*x^2*y^2 - y^4)^(1/2))/(m^2 + 2*m*x - n^2 + x^2 + y^2));
b(4)= -2*atan(((- m^2 + 2*m*n - n^2 + x^2 + y^2)*(m^2 + 2*m*n + n^2 - x^2 - y^2))^(1/2)/(- m^2 + 2*m*n - n^2 + x^2 + y^2));
以a(3)为例,假设x=20,其它参数未知,则:
a(3)=subs(a(3),x,20) ; 即可将x取值替换为20;
假设 x=20 , y=30 ,其它参数未知,则:
a(3)=subs(a(3),{x,y},{20,30});
2、求解矩阵方程:
a=[1 0;0 2];
b=[1;3];
syms x1 x2;
y=a*[x1;x2]+b;
s=solve(y(1),y(2),'x1','x2');
s.x1 %w2值
s.x2 %w2值
3、
Matlab求解二阶微分方程组:

m=1;
g=9.8;
k=100;
l0=1.1;
x0=[0.1 0 0 0]; %初始值;
% 定义 x(1)=l, x(2)=l', x(3)=a, x(4)=a';
dx=@(t,x)[x(2); (m*x(1)*x(4)^2-m*g*cos(x(3))-k*(x(1)-l0))/m; x(4); (-2*m*x(1)*x(2)*x(4) + m*g*x(1)*sin(x(3)))/(m*x(1)^2)];
[t,x]=ode15s(dx,[0 10],x0);
lstr = { '\itl', '{\itl}''', '\alpha', '\alpha''' };
for i=1:length(lstr)
subplot(2,2,i)
plot(t, x(:,i));
xlabel('Time')
ylabel( lstr{i} )
end



