poj3233 题解矩阵乘法矩阵快速幂

题意：求S = A + A² + A³ + … + A^k.(mod m)

这道题很明显可以用矩阵乘法，但是这道题的矩阵是分块矩阵，

　　分块矩阵概念如下：当一个矩阵A中的单位元素aij不是一个数值而是一个矩阵是A矩阵称为分块矩阵，在性质满足的前提下依然满足矩阵加法乘法。例如矩阵乘法A×B，将B按行分块，可以看成矩阵A乘列向量，其中B中每个元素是一个行向量；将A按列分块同理。

　　简单地说，就是矩阵里的元素还是个矩阵。这道题我们可以像这样构建矩阵：

　　　　　　　　∵S_n=S_n-1+A^k∴有如下转移图

　　　　　　　　写出邻接矩阵（下图用E表示单位矩阵也就是"1”，0表示全是0的矩阵也就是“0”，A即为输入的矩阵）

　　　　　　　　也就有：

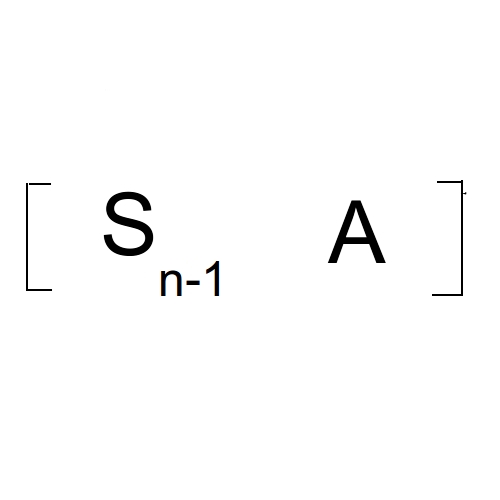
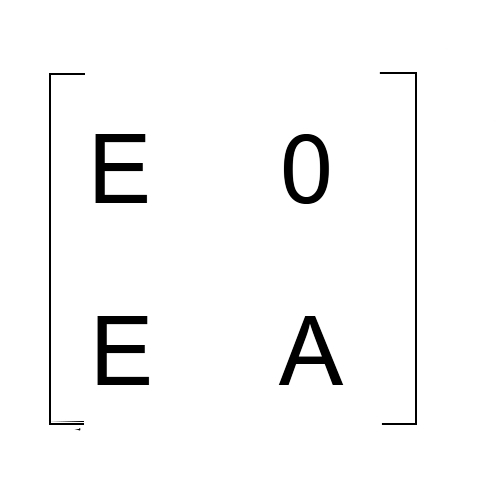
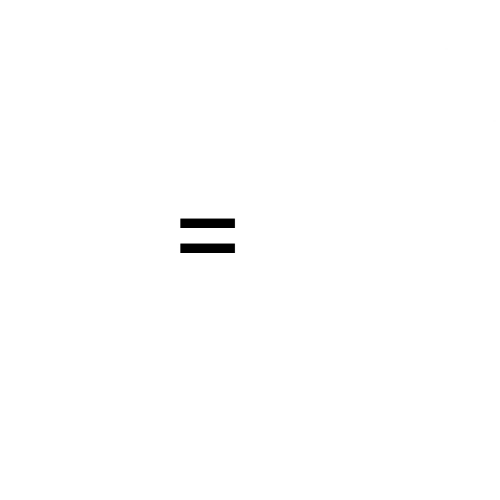
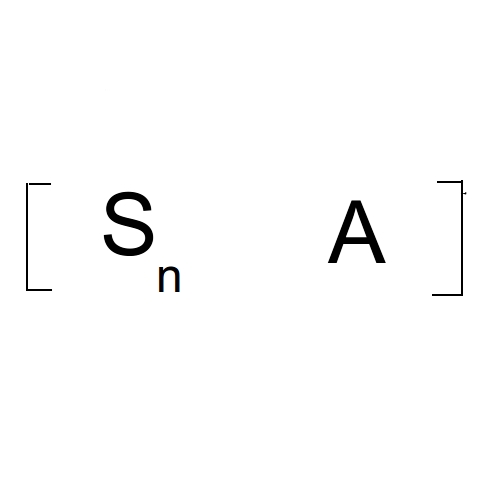
　　　　　　　　最终答案是：

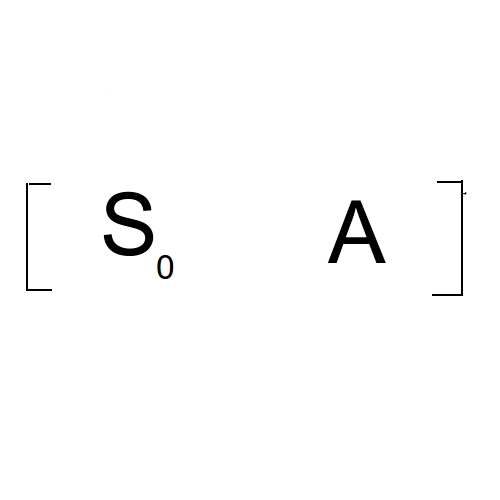
所以，最终C++程序只需要重载运算符就可以轻松AC了

而另一种做法，也就是二分加矩阵快速幂则需要较长时间（800+MS）

  1 #include <iostream>
  2 #include <algorithm>
  3 #include <cmath>
  4 #include <ctime>
  5 #include <cstring>
  6 #include <cstdio>
  7 #include <cstdlib>
  8 
  9 using namespace std;
 10 
 11 int    n,k,m;
 12 
 13 class Matrix
 14 {
 15     public:
 16     int    val[31][31];
 17     int    x,y;
 18 
 19     Matrix()
 20     {
 21         memset(val,0,sizeof(val));
 22         x=y=0;
 23         return ;
 24     }
 25     
 26     void    set_E()
 27     {
 28         int    i;
 29         for(i=1;i<=x;++i)
 30             val[i][i]=1;
 31         return ;
 32     }
 33     
 34     Matrix operator*(Matrix b)
 35     {
 36         int    i,j,k;
 37         Matrix    c;
 38         c.resize(x,b.y);
 39     
 40         for(k=1;k<=b.x;++k)
 41         for(i=1;i<=x;++i)
 42         if(val[i][k])//不加这行就要340+MS
 43         for(j=1;j<=b.y;++j)
 44             c.val[i][j]=(c.val[i][j]+val[i][k]*b.val[k][j])%m;
 45         return c;
 46     }
 47 
 48     Matrix    operator+(Matrix b)
 49     {
 50         Matrix    c;
 51         c.resize(max(x,b.x),max(y,b.y));
 52         int    i,j;
 53         
 54         for(i=1;i<=c.x;++i)
 55         for(j=1;j<=c.y;++j)
 56             c.val[i][j]=(val[i][j]+b.val[i][j])%m;
 57         
 58         return c;
 59     }
 60 
 61     void    resize(const int & _x,const int & _y)
 62     {
 63         x=_x,y=_y;
 64         return ;
 65     }
 66 }A;
 67 
 68 class    Matrix_Plus
 69 {
 70     public:
 71     Matrix    val[3][3];
 72     int    x,y;
 73     
 74     Matrix_Plus()
 75     {
 76         memset(val,0,sizeof(val));
 77         x=y=0;
 78         return ;
 79     }
 80 
 81     void    set_E()
 82     {
 83         int    i;
 84         for(i=1;i<=x;++i)
 85             val[i][i].set_E();
 86         return ;
 87     }
 88 
 89 
 90     Matrix_Plus operator*(Matrix_Plus b)
 91     {
 92         Matrix_Plus    c;
 93         int    i,j,k;
 94         c.resize(x,b.y);
 95         
 96         for(k=1;k<=b.x;++k)
 97         for(i=1;i<=x;++i)
 98         for(j=1;j<=b.y;++j)
 99             c.val[i][j]=c.val[i][j]+val[i][k]*b.val[k][j];
100         return c;
101     }
102     
103     Matrix_Plus operator^(int    p)
104     {
105         Matrix_Plus    r,base;
106         r.resize(2,2);
107         r.val[1][1].resize(n,n);
108         r.val[1][2].resize(n,n);
109         r.val[2][1].resize(n,n);
110         r.val[2][2].resize(n,n);
111         r.set_E();
112         base=*this;
113         
114         while(p)
115         {
116             if(p&1)
117                 r=r*base;
118             base=base*base;
119             p>>=1;
120         }
121         
122         return r;
123     }
124     
125     void    resize(const int & _x,const int & _y)
126     {
127         x=_x,y=_y;
128         return ;
129     }
130 
131 }S,A_;
132         
133 int main()
134 {    
135     int    i,j;
136     
137     scanf("%d%d%d",&n,&k,&m);
138     A.resize(n,n);
139     
140     for(i=1;i<=n;++i)
141     {
142         for(j=1;j<=n;++j)
143         {
144             scanf("%d",&A.val[i][j]);
145         }
146     }
147     
148     S.resize(1,2);
149     S.val[1][2]=A;
150     S.val[1][1].resize(n,n);
151     S.val[1][2].resize(n,n);
152     
153     A_.resize(2,2);
154     A_.val[1][1].resize(n,n);
155     A_.val[1][2].resize(n,n);
156     A_.val[2][1].resize(n,n);
157     A_.val[2][2].resize(n,n);
158     A_.val[1][1].set_E();
159     A_.val[2][1].set_E();
160     A_.val[2][2]=A;    
161     S=S*(A_^k);
162     
163     for(i=1;i<=n;++i)
164     {
165         for(j=1;j<=n;++j)
166             printf("%d ",S.val[1][1].val[i][j]);
167         printf("\n");
168     }
169     return 0;
170 }

posted @ 2015-08-04 20:44 Gster 阅读(440) 评论(1) 编辑收藏举报

刷新页面返回顶部

Gster

poj3233 题解 矩阵乘法 矩阵快速幂

公告

poj3233 题解矩阵乘法矩阵快速幂