dsu on tree(树上启发式合并)
一直都没出过算法详解,昨天心血来潮想写一篇,于是 dsu on tree 它来了
1、前置技能
1.链式前向星(vector 建图)
2.dfs 建树
3.剖分轻重链,轻重儿子
| 重儿子 | 一个结点的所有儿子中拥有最多子树的儿子 |
|---|---|
| 轻儿子 | 一个结点的所有儿子中不是重儿子的儿子 |
| 重边 | 父亲与重儿子的连边 |
| 轻边 | 父亲与轻儿子的连边 |
| 重链 | 一堆重边连接而成的链 |
| 轻链 | 一堆轻边连接而成的链 |
2、什么是 dsu on tree(树上启发式合并) ?
dsu on tree 其实就是个优雅的暴力算法,和它一起共被称为优雅暴力的算法还有莫队
所谓优雅的暴力大概是指:“优雅思想,暴力的操作”
例如莫队我们知道它是将整个区间分块,再将询问的区间排序,最后暴力的维护所有询问的区间
其中 "整个区间分块,询问的区间排序" 为优雅的思想,而 "暴力的维护所有询问的区间" 为暴力的操作
因为需要将询问的区间排序,我们就需要先将询问的区间保存下来,也就是要离线
dsu on tree 和莫队类似,也需要离线(它们同属于静态算法)
dsu on tree 优雅的思想:
对于以 u 为根的子树
①. 先统计它轻子树(轻儿子为根的子树)的答案,统计完后删除信息
②. 再统计它重子树(重儿子为根的子树)的答案 ,统计完后保留信息
③. 然后再将重子树的信息合并到 u上
④. 再去遍历 u 的轻子树,然后把轻子树的信息合并到 u 上
⑤. 判断 u 的信息是否需要传递给它的父节点(u 是否是它父节点的重儿子)
dsu on tree 暴力的操作
dsu on tree 暴力的操作体现于统计答案上(不同的题目统计方式不一样)
3、dsu on tree 的过程演示及代码
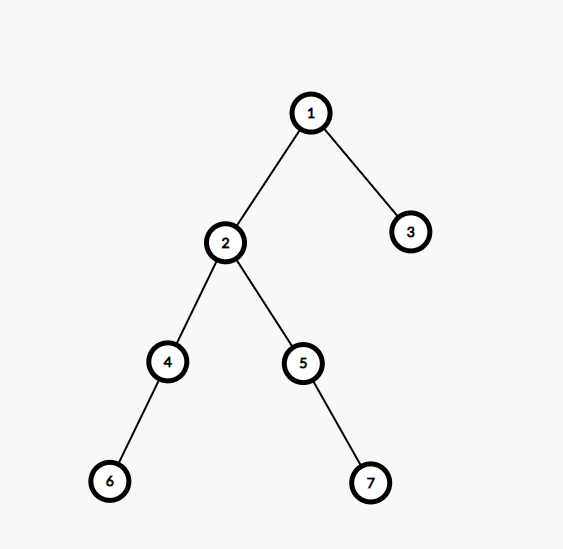
1.图示
1 的重儿子为 2,轻儿子为 3
2 的重儿子为 4,轻儿子为 5
3 没有重儿子,没有轻儿子
4 的重儿子为 6,没有轻儿子
5 的重儿子为 7,没有轻儿子
6 没有重儿子,没有轻儿子
7 没有重儿子,没有轻儿子
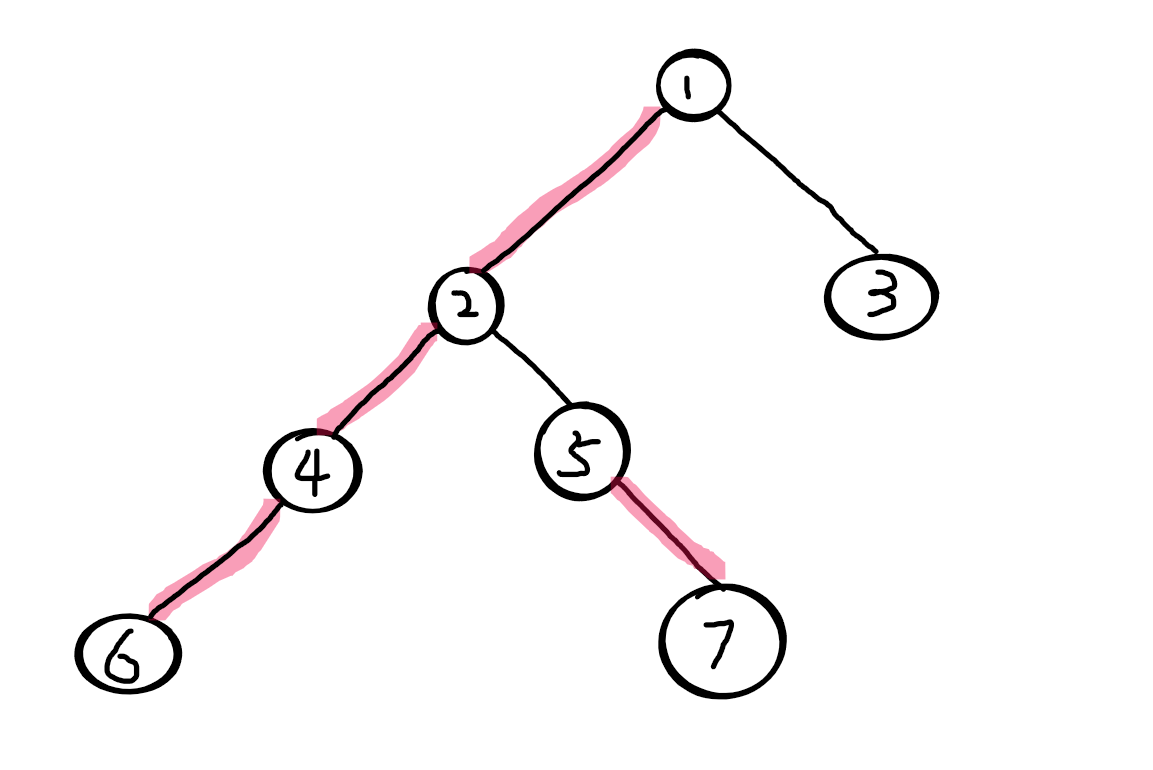
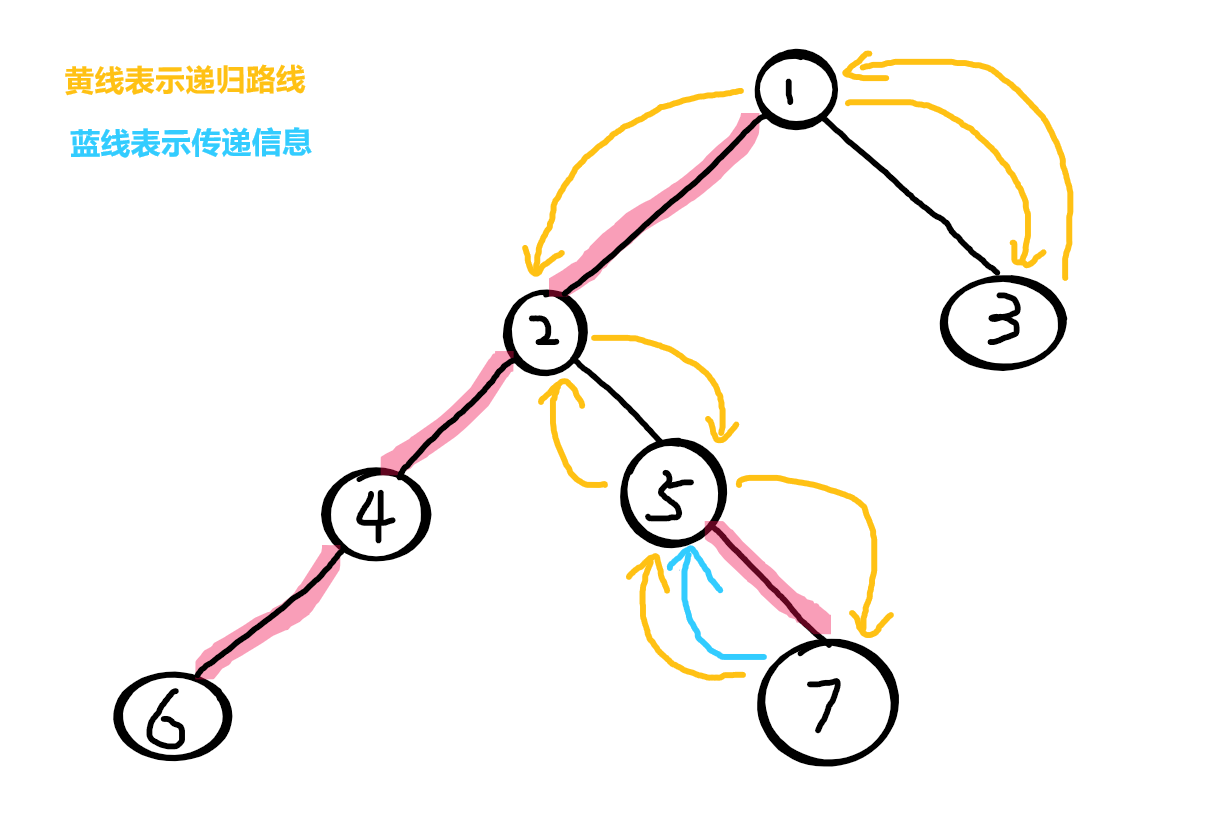
为了更好观看,我们将节点与其重儿子的连线描红
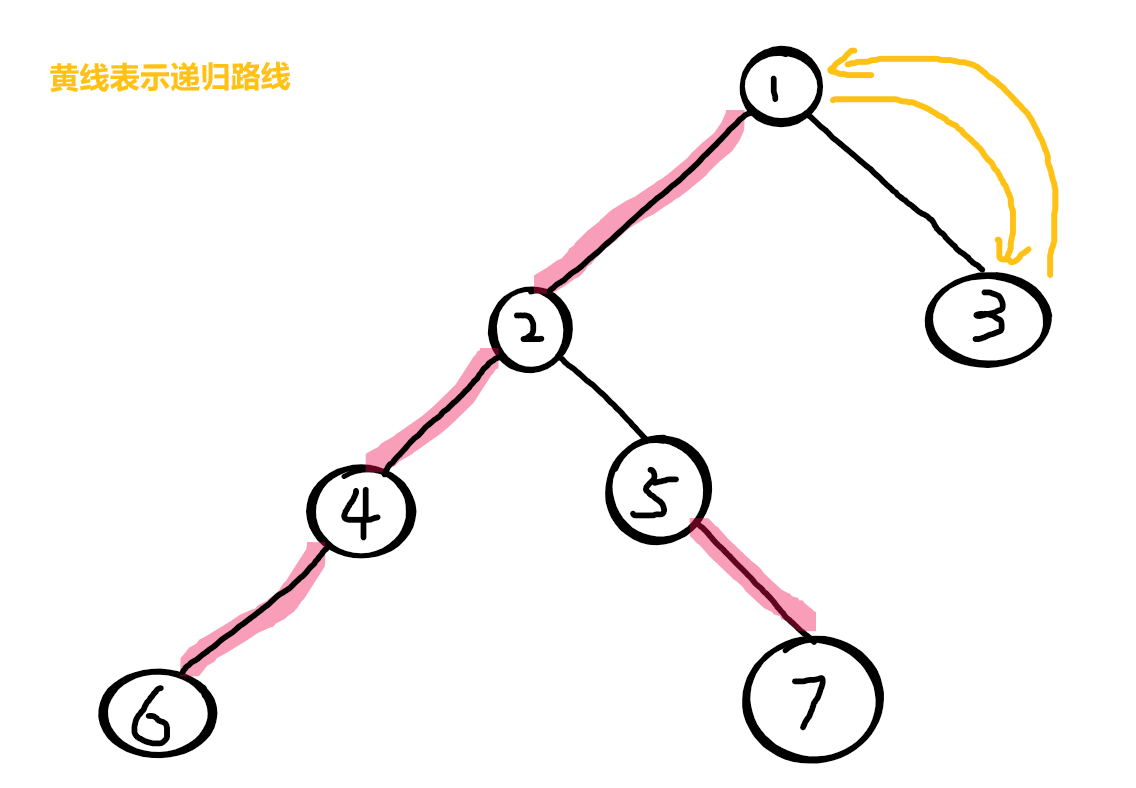
我们从根节点1进入,先找1的轻儿子,发现3,进入3
3没有别的儿子可以进入了,于是统计3的信息
统计完后即将返回父节点 1
因为1-3的边没有被描红边、3不是1的重儿子(不传递3的信息),所以删除3的信息再返回 1
发现1没有别的轻儿子了,就找重儿子,发现2,进入2
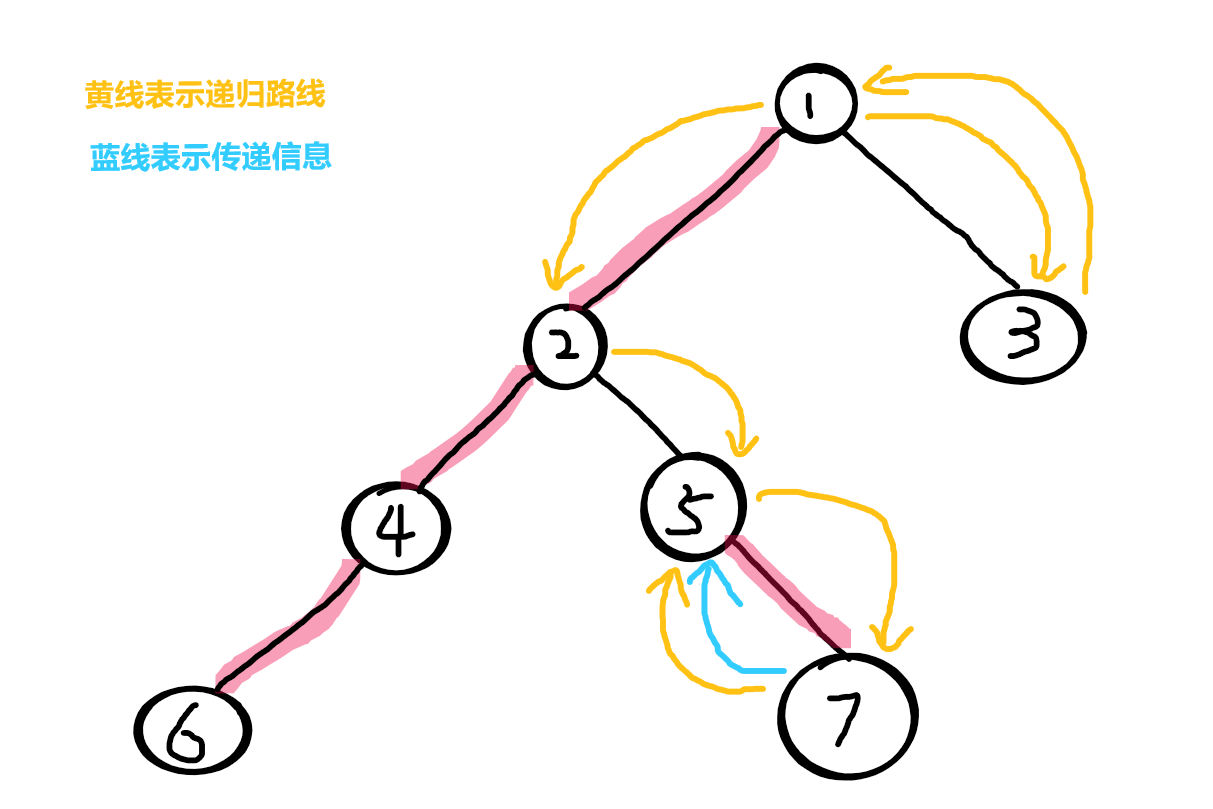
进入2后,再找2的轻儿子,发现5,进入5
发现5没有轻儿子了,就找重儿子,发现7,进入 7
7 没有别的儿子可以进入了,于是统计 7 的信息
统计完后即将返回父节点 5
因为边5-7 有被描红边、7是5的重儿子,所以保留7的信息直接返回 5(传递7的信息的给5)
5 所有儿子都进入过了,于是统计 5 的信息
统计完后即将返回父节点 2
因为边2-5 没有被描红边、5不是2的重儿子,所以删除5的信息再返回 2
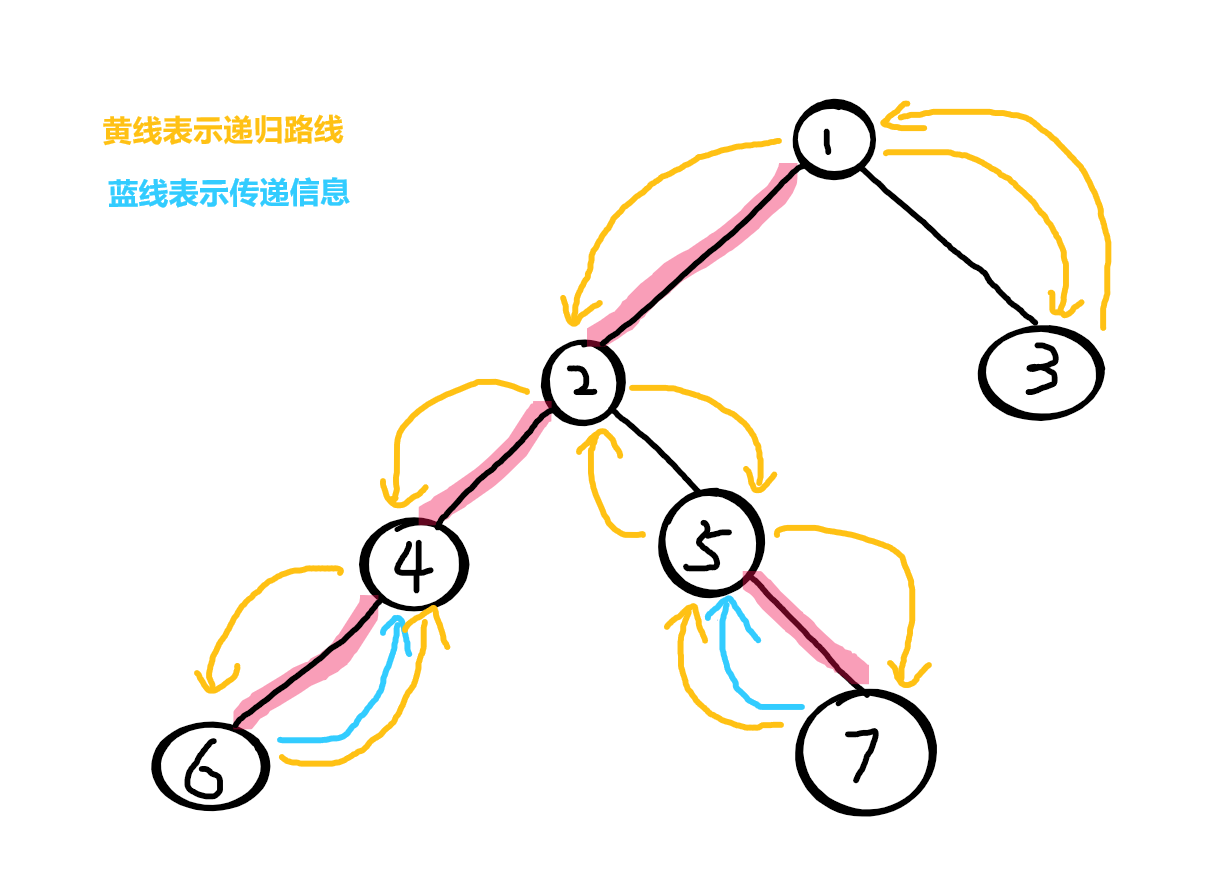
发现2没有其它轻儿子了,就找重儿子,发现4,进入4
发现4没有其它轻儿子了,就找重儿子,发现6,进入6
6 没有别的儿子可以进入了,于是统计 6 的信息
统计完后即将返回父节点 4
因为边4-6 有被描红边,6是4的重儿子,所以保留6的信息直接返回 4(传递6的信息的给4)
4 所有儿子都进入过了,于是统计 4 的信息
统计完后即将返回父节点 2
因为边2-4 有被描红边,4是2的重儿子,所以保留4的信息直接返回2(传递4的信息的给2)
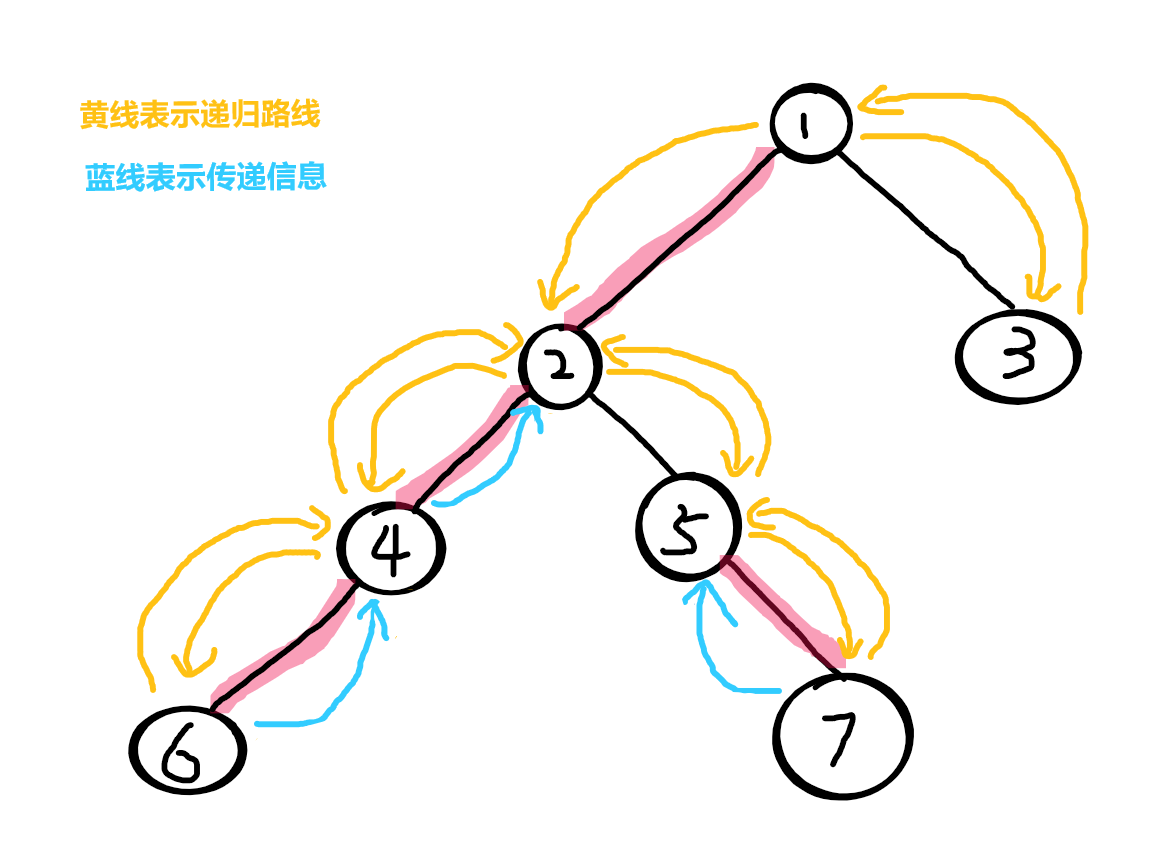
2 所有儿子都进入过了,于是统计 2 的信息
2 接受了4传递的信息,但是并没有接受5传递给它的信息(被删除了)
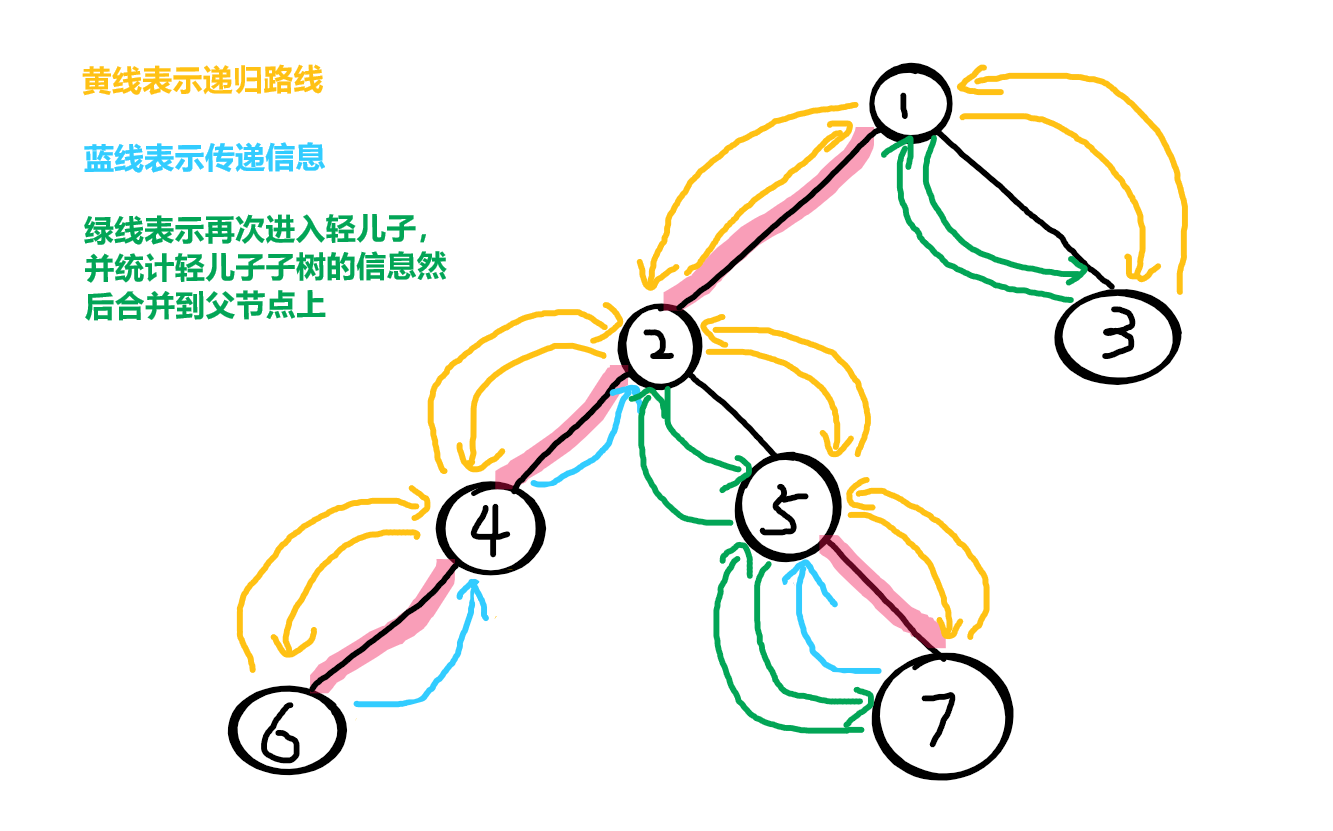
于是 2 再进入5(轻儿子),统计一遍以 5 为根的子树的信息,再将该信息合并到 2上
统计完后 2 后即将返回父节点 1
因为边1-2 有被描红边,2是1的重儿子,所以保留2的信息直接返回1(传递2的信息的给1)
1 所有儿子都进入过了,于是统计 1 的信息
1 接受了2传递的信息,但是并没有接受3传递给它的信息(被删除了)
于是 1 再进入3(轻儿子),统计一遍以 3 为根的子树的信息,再将该信息合并到 1 上
至此,整个 dsu on tree 的过程结束
2.代码
struct Edge{
int nex , to;
}edge[N << 1];
int head[N] , TOT;
void add_edge(int u , int v) // 链式前向星建图
{
edge[++ TOT].nex = head[u] ;
edge[TOT].to = v;
head[u] = TOT;
}
int sz[N]; // sz[u] 表示以 u 为根的子树大小
int hson[N]; // hson[u] 表示 u 的重儿子
int HH; // HH 表示当前根节点的重儿子
void dfs(int u , int far)
{
sz[u] = 1;
for(int i = head[u] ; i ; i = edge[i].nex) // 链式前向星
{
int v = edge[i].to;
if(v == far) continue ;
dfs(v , u);
sz[u] += sz[v];
if(sz[v] > sz[hson[u]]) hson[u] = v; // 选择 u 的重儿子
}
}
void calc(int u , int far , int val) // 统计答案
{
if(val == 1) ...; // val = 1,则添加信息
else ...; // val = -1,则删除信息
......
for(int i = head[u] ; i ; i = edge[i].nex)
{
int v = edge[i].to;
if(v == far || v == HH) continue ; // 如果 v 是当前根节点的重儿子,则跳过
calc(v , u , val);
}
}
void dsu(int u , int far , int op) // op 等于0表示不保留信息,等于1表示保留信息
{
for(int i = head[u] ; i ; i = edge[i].nex)
{
int v = edge[i].to;
if(v == far || v == hson[u]) continue ; // 如果 v 是重儿子或者父亲节点就跳过
dsu(v , u , 0); // 先遍历轻儿子 ,op = 0 :轻儿子的答案不做保留
}
if(hson[u]) dsu(hson[u] , u , 1) , HH = hson[u];
// 轻儿子都遍历完了,如果存在重儿子,遍历重儿子(事实上除了叶子节点每个点都必然有重儿子)
// op = 1 , 保留重儿子的信息
// 当前是以 u 为根节点的子树,所以根节点的重儿子 HH = hson[u]
calc(u , far , 1); // 再次遍历轻儿子统计答案
HH = 0; // 遍历结束 ,即将返回父节点,所以取消标记 HH
if(!op) calc(u , far , -1); // 如果 op = 0,则 u 对于它的父亲来说是轻儿子,不需要将信息传递给它的父亲
}
4.经典例题讲解
5.难题进阶
这是道较难的题,听说这也是 dsu on tree 的发明人专门为这个算法出的题
| 题目编号 | 题目链接 | 题解链接 |
|---|---|---|
| CF741D | https://codeforces.com/contest/741/problem/D | https://www.cnblogs.com/StarRoadTang/p/14028301.html |
┏┛ ┻━━━━━┛ ┻┓
┃ ┃
┃ ━ ┃
┃ ┳┛ ┗┳ ┃
┃ ┃
┃ ┻ ┃
┃ ┃
┗━┓ ┏━━━┛
┃ ┃ 神兽保佑
┃ ┃ 代码无BUG!
┃ ┗━━━━━━━━━┓
┃ ┣┓
┃ ┏┛
┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
┃ ┫ ┫ ┃ ┫ ┫
┗━┻━┛ ┗━┻━┛