牛客练习赛64 D宝石装箱

题面

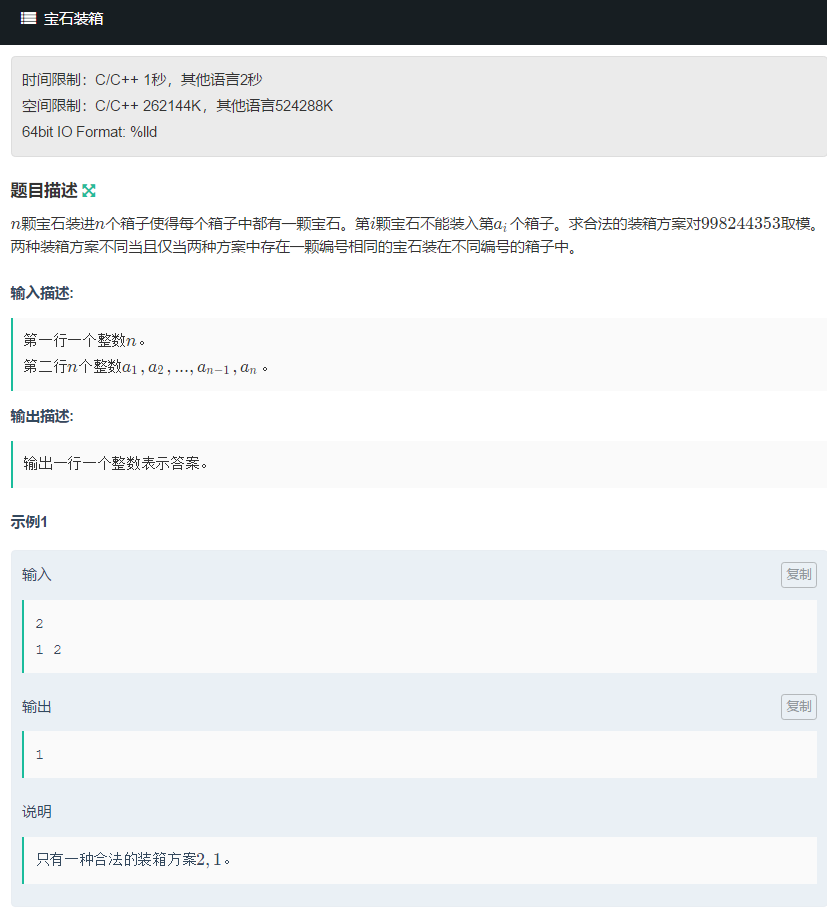
题目链接

https://ac.nowcoder.com/acm/contest/5633/D

题目大意

n 颗宝石装进 n 个箱子使得 , 每个箱子中都有一颗宝石

其中第 i 颗宝石不能装入第 ai 个箱子 , 求合法的装箱方案数。

解题思路

总的装箱方案为 N! ，答案 = 总方案数 - $\sum ^{n}_{i=1}f\left( i\right)  $ , 其中 f(x) 表示 x 个箱子不合法的方案数

我们定义 dp[i][j] 表示前 i 个箱子有 j 个放了不合法的宝石 , 其它 n - i 个箱子先不放宝石的方案数

那么 $dp_{ij}=dp_{i-1j}+dp_{i-1j-1}\times a_{i}$ , 前 n 个箱子至少有 i 个不合法的方案数为 $dp_{ni}\times \left( n-i\right) !$

于是根据容斥可得

\begin{aligned}ans=n!-\sum ^{n}_{i=1}\left( -1\right) ^{i}\times dp_{ni}\times \left( n-i\right) !\\
=\sum ^{n}_{i=0}\left( -1\right) ^{i}\times dp_{ni}\times \left( n-i\right) !\end{aligned}

因为我们最后只需要用到 dp[n][i]，而 dp[i][j] 又只会由 dp[i - 1][j] 、dp[i - 1][j - 1] 转移得到

所以我们可以用背包问题优化空间方法的方法优化它

AC_Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 8e3 + 10;
const int mod = 998244353;
int a[N] , fac[N] , dp[N];
void init()
{
    fac[0] = 1;
    for(int i = 1 ; i <= N - 10 ; i ++) fac[i] = fac[i - 1] * i % mod;
}
signed main()
{
    ios::sync_with_stdio(false);
    init();
    int n , m = 0;
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)
    {
        int x;
        cin >> x;
        a[x] ++ ;
    } 
    dp[0] = 1;
    for(int i = 1 ; i <= n ; i ++)
        for(int j = i ; j >= 1 ; j --)
            dp[j] += dp[j - 1] * a[i] , dp[j] %= mod;
    int ans = 0;
    for(int i = 0 ; i <= n ; i ++)
    {
        if(i & 1) ans -= dp[i] * fac[n - i] ; 
        else ans += dp[i] * fac[n - i];
        ans = (ans + mod) % mod;
    }
    cout << ans << '\n';
    return 0;
}