AtCoder Beginner Contest 158E 、164D

上次 Atcoder ABC164的 D 题写了个 dp 水过了

赛后P神在群里说D题是 ABC158 E 题弱化版，正解复杂度是O(n) / O(nlogn)

于是我拿我的 dp 尝试了下这道 E 题，果不其然超时了（我好菜T^T）

为了解决它，我又花了十分钟研究了一下，终于顺利用正解 A 掉啦

先上弱化版的

题面

题目链接

https://atcoder.jp/contests/abc164/tasks/abc164_d

题目大意

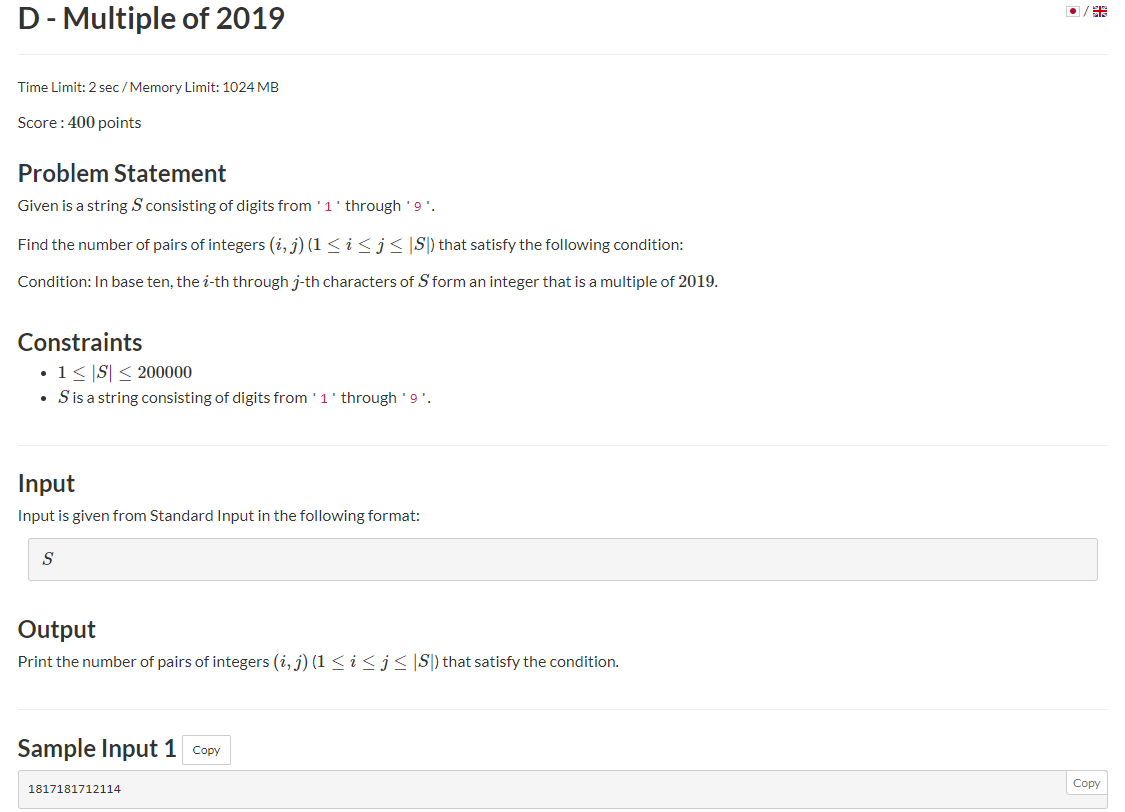
给你一个仅包含数字的字符串 S

问你有多少对 (i , j) 使得由 S[i]...S[j] 组成的数能被 2019 整除

解题思路

这题只讲下 dp 的做法

我们定义 dp[i][j] 表示前 i 个数构成以 i 结尾，模 2019 = j 的方案数

定义 nd = ( j * 10 + s[i] - '0' ) % 2019 ，那么 dp[ i ][ nd ] += dp[ i - 1 ][ j ] , ans += dp[ i ][ 0 ]

因为 dp[ i ] 只会由 dp[ i - 1 ] 转移得到

所以为了节省空间我们可以使用滚动数组，也可以另开两个数组 cnt 、pre 分别维护 dp[i] 和 dp[ i - 1 ]

复杂度 O ( 2019 * n )

AC_Code

#include<bits/stdc++.h>
using namespace std;
const int N = 3e3 + 10 , M = 2e5 + 10;
int pre[N] , cnt[N] , ans;
string s; 
signed main()
{
    cin >> s ;
    for(auto i : s)
    {
        int x = i - '0';
        memset(cnt , 0 , sizeof(cnt));
        for(int j = 0 ; j <= 2018 ; j ++)
        {
            int nd = (j * 10 + x) % 2019;
            if(!nd) ans += pre[j];
            cnt[nd] += pre[j];
        }
        cnt[x] ++ ;
        for(int j = 0 ; j <= 2018 ; j ++) pre[j] = cnt[j]; 
    }
    cout << ans << '\n'; 
    return 0;
}

接下来上强化版的

题面

题目链接

https://atcoder.jp/contests/abc158/tasks/abc158_e

题目大意

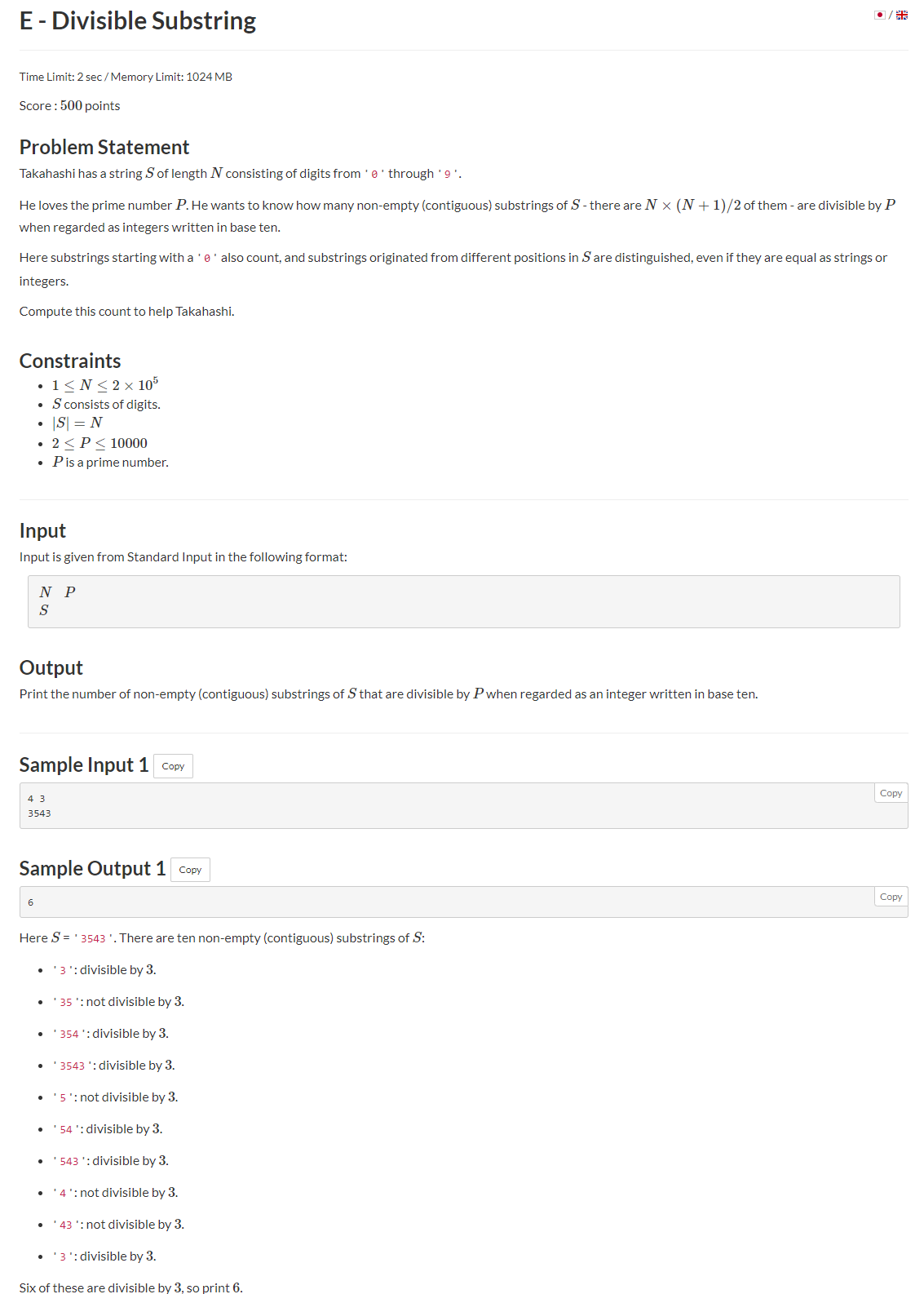
给你一个仅包含数字长度为 N 字符串 S 和 一个质数 P

问你有多少对 (i , j) 使得由 S[i]...S[j] 组成的数能被 P 整除

解题思路

这题就不能用上述做法了，因为 P 的范围为1e4 ， N 的范围为 2e5 

于是我们可以想到统计一个前缀来操作

即当前缀重复出现时，重复端点之间的区间构成的数字可被2019整除

我们用 sum 表示前 i 个数的前缀 , cnt 来维护前缀出现的次数，那么 ans += cnt [ sum[i] ]

是不是很简单呢？好吧这样其实是不行的，举个栗子：

当 S = 268646 ， P = 2019 时 ， 答案应该为 1 ，因为 68646 可以整除 2019

但是此时它的前缀模2019分别为 0 , 2 , 26 , 268 , 667 , 617 , 119

我们会发现它的前缀并没有重复出现的情况，为什么呢？

因为在我们统计到第一个 6 时，此时 i = 2，前缀为26，这个 6 是作为个位部分被统计的

而在 68646 中我们是希望它作为万位部分被统计，所以维护前缀是行不通的

但是，我们可以去维护它的后缀 suf ，即 ans += cnt [ suf[i] ] 

为什么维护后缀就可以呢？再举个栗子：当 S = 68646111

从后往前枚举，对于68646 我们希望第一个 6 是个位，最后一个 6 是万位

但若第一 6 是千位，最后一个 6 是千万位，则构成的数为 68646000

根据同余定理当 P 和 10互质时，若 xxxx0000 % p = 0 则 xxxx % p = 0，所以维护后缀是可以的

于是我们只要对 P = 2 || P = 5 时特判一下(判断个位是否整除P)，其它情况维护后缀就可以了

AC_Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n , mod , now , ans , base = 1;
string s;
map<int , int>vis;
signed main()
{
    cin >> n >> mod >> s ;
    if(mod == 2 || mod == 5)
    {
        for(int i = 0 ; i < n ; i ++)
        {
            int x = s[i] - '0';
            if(x % mod == 0) ans += i + 1 ;
        }
        return cout << ans << '\n' , 0;
    }
    reverse(s.begin() , s.end()) , vis[0] = 1;    
    for(auto i : s)
    {
        int x = i - '0';
        now = (now + x * base) % mod;
        ans += vis[now]; 
        vis[now] ++ , base *= 10 , base %= mod;
    }
    cout << ans << '\n';
    return 0;
}