Codeforces Round #613 (Div. 2)
A. Mezo Playing Zoma
题目链接:https://codeforces.com/contest/1285/problem/A
题意:
你的初始位置位于0,给你一串只包含 LR 的字符串,L表示你的位置可以-1(或者不变),R表示你的位置可以+1(或者不变),问你最多可以到达多少种不同地方
分析:
统计 LR 的个数 , 答案为 L + R + 1;

#include<bits/stdc++.h> using namespace std; #define rep(i , a , b) for(int i = a ; i <= b ; i ++) #define ios std::ios::sync_with_stdio(false); const int N = 2e5 + 10; char s[N]; int main() { ios; int n ; cin >> n; cin >> s + 1; int L = 0 , R = 0; rep(i , 1 , n) if(s[i] == 'L') L ++; else R ++; cout << L + R + 1 << '\n'; return 0; }
B. Just Eat It!
题目链接:https://codeforces.com/contest/1285/problem/B
题意:
总共有n个糖果,每个糖果都有自己的美味值(可能为负),有两个人,一个取全部,一个取片段(不能全取),如果取片段的最大美味值大于取全部的美味值输出YES,否则输出NO。
分析:
因为取片段的不能取全部,所以我们只要对 1 - (n - 1) 和 2 - n 的最大字段和进行操作再与sum判断即可

#include<bits/stdc++.h> using namespace std; #define rep(i , a , b) for(int i = a ; i <= b ; i ++) #define ios std::ios::sync_with_stdio(false); #define ll long long const int N = 2e5 + 10; ll dp[N] , a[N]; ll get(int l , int r) { memset(dp , 0 , sizeof(dp)); ll res = 0; rep(i , l , r) { dp[i] = max(dp[i - 1] + a[i] , max(0LL , a[i])); res = max(res , dp[i]); } return res; } int main() { ios; int t ; cin >> t; while(t --) { int n ; ll sum = 0; cin >> n; rep(i , 1 , n) cin >> a[i] , sum += a[i]; ll ans = get(1 , n - 1); ans = max(ans , get(2 , n)); if(sum > ans) cout << "YES" << '\n'; else cout << "NO" << '\n'; } return 0; }
赛后用二维dp也过了
其中dp[i][0]表示前i个数的最大字段和,dp[i][1]表示得到这个最大字段和一共用了多少个数也过了,然后遍历判断dp[i][0]是否大于sum&&dp[i][1]是否小于n

#include<bits/stdc++.h> using namespace std; #define ll long long const int N = 2e5 + 10; ll a[N] , dp[N][2]; int main() { ll t; cin >> t; while(t --) { ll n ; cin >> n; for(ll i = 1 ; i <= n ; i ++) dp[i][1] = dp[i][0] = a[i] = 0; ll sum = 0; ll flag = 0; for(ll i = 1 ; i <= n ; i ++) { cin >> a[i] , sum += a[i]; if(a[i] <= 0) flag = 1; } int cnt = 0; for(ll i = 1 ; i <= n ; i ++) { dp[i][0] = max(dp[i - 1][0] + a[i] , max(0LL , a[i])); if(dp[i][0] == 0) cnt = 0; if(dp[i][0] == a[i]) cnt = 1; else cnt = dp[i - 1][1] + 1; dp[i][1] = cnt; } ll ha = 0; for(ll i = 1 ; i <= n ; i ++) if(dp[i][0] >= sum && dp[i][1] < n) { ha = 1; break; } if(ha) cout << "NO" << '\n'; else cout << "YES" << '\n'; } return 0; }
C. Fadi and LCM
题目链接:https://codeforces.com/contest/1285/problem/C
题意:
给你一个 X,求得两个数 a , b 使得lcm(a , b) = X 并且 max(a , b) 尽可能小
分析:
因为 X 只有 1e12 , 所以直接暴力处理sqrt(X) 内X的所有因子是否为答案

#include<bits/stdc++.h> using namespace std; #define ll long long const int N = 2e5 + 10; ll a[N] , dp[N][2]; ll lcm(ll a , ll b) { return a * b / __gcd(a , b); } int main() { ll x; cin >> x; ll ans1 = 0x3f3f3f3f3f3fll; ll ans2 = 0x3f3f3f3f3f3fll; for(ll i = 1 ; i <= sqrt(x) ; i ++) { if(x % i == 0) { if(lcm(x / i , i ) == x && max(ans1 , ans2) > max(x / i , i)) ans1 = i , ans2 = x / i; } } cout << ans1 << " " << ans2 << '\n'; return 0; }
D. Dr. Evil Underscores
题目链接:https://codeforces.com/contest/1285/problem/D
题意:
给你一个含有 n 个元素的数组,让你求得一个数 X ,使得 X 异或这个数组中的每个数的最大值尽可能小
分析:
01字典树的模板题。
比赛的时候常规写法先 insert 后 search 因为要占用很大空间所以一直 runtime error,把空间改大又一直爆内存,所以这个问题卡了老久后直接换了种写法
用 dfs 查找从树根往下查找(其实就是边建树边search)。
自己用数组模拟过程写的巨丑,于是参考了一下别人的vector写法

#include<bits/stdc++.h> using namespace std; #define ll long long #define pb push_back const ll N = 2e5 + 10; ll n ; ll dfs(vector<ll> vec , ll now) { if(now < 0 || !vec.size() ) return 0; vector<ll>one , two; for(ll i = 0 ; i < vec.size() ; i ++) { if((vec[i] >> now) & 1) one.pb(vec[i]); else two.pb(vec[i]); } if(!one.size()) return dfs(two , now - 1); else if(!two.size()) return dfs(one , now - 1); else return (1LL << now) + min(dfs(one , now - 1) , dfs(two , now - 1)); } int main() { cin >> n; vector<ll>vec; for(int i = 1 ; i <= n ; i ++) { ll x; cin >> x; vec.pb(x); } cout << dfs(vec , 30) << '\n'; return 0; }
赛后又经过三次的runtime error 后把最初的写法也 AC 了。。。

#include<bits/stdc++.h> using namespace std; #define ll long long #define pb push_back const int N = 2e6 + 10; int tot = 0; int trie[N][31]; int a[N]; void insert(int x) { int root = 0; for(int i = 30 ; ~i ; i --) { int ch = x >> i & 1; if(!trie[root][ch]) trie[root][ch] = ++ tot; root = trie[root][ch]; } } int search(int root , int bit) { if(bit < 0) return 0; if(!trie[root][1]) return search(trie[root][0] , bit - 1); if(!trie[root][0]) return search(trie[root][1] , bit - 1); else return (1 << bit) + min(search(trie[root][1] , bit - 1) , search(trie[root][0] , bit - 1)); } int main() { int n ; cin >> n; for(int i = 1 ; i <= n ; i ++) cin >> a[i] , insert(a[i]); cout << search(0 , 30) << '\n'; return 0; }
E. Delete a Segment
题目链接:https://codeforces.com/contest/1285/problem/E
题意:
给你 n 个区间,每个区间有自己的 Li 和 Ri,如果区间相交则他们将合并为同一个区间,现在你可以任意删除一个区间,问删除后最大可以剩下多个个区间
分析:
开始我们先认为所有可合并的区间已经合并结束
然后我们创建一个数组 add ,其中add[i]表示删除i这个区间后会新增加几个区间
假设我们要删除的区间为 X , 那么和X有关的区间大致情况为以下几种
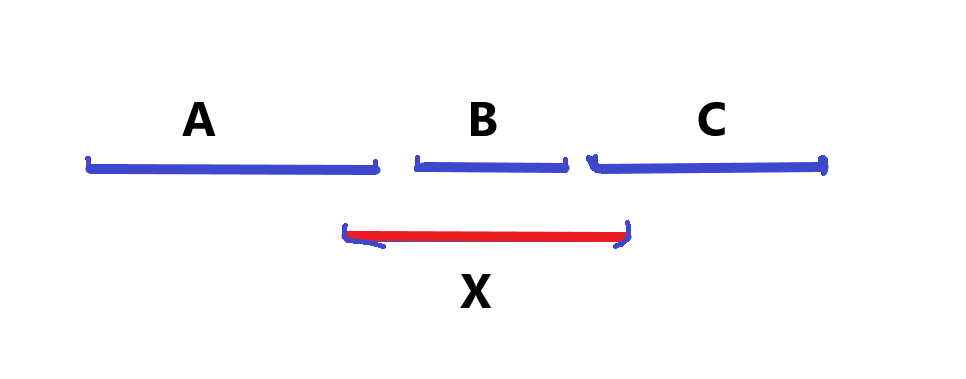
对于上图若删除 X 则会新增加三个区间,所以add[x] = 3,那么我们要怎么计算这个add[x]呢?
假设我们只考虑端点每个区间的左右端点。
首先我们观察A , B 会发现 La < Lx , Ra > Lx , 且 Ra的下一个端点为Lb(左端点),所以 X 连接了 AB。对于BC也一样。
当碰到Ra的时候,Lx已经出现过,且Ra的下一个端点Lb为左端点,所以A,B才能连接。
而在这个过程中,Rx是一直没有出现的。
当然还会有下面这样的情况。
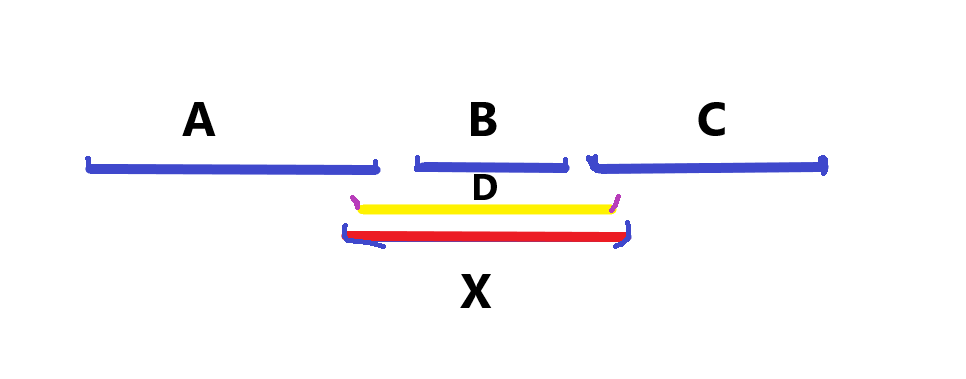
而对于这种情况我们会发现,当Ra出现时除了La外还有Lx、Ld存在,而实际上D区间对于AB的连接是多余的(有X在),当然也可以理解成X对AB的连接是多余的,对于这种情况不论我们删除哪一个都不会改变区间的数量。
One所以要满足X能唯一连接AB的条件为:①Ra的下一个端点为左端点 ②当Ra出现的时候,除了La,只能有一个端点存在(即把La删除后只剩下一个Lx)。对BC同理。
Two还有需要注意的是如果第i个区间是完全独立的区间,则删除区间 i 后区间个数会 -1,即下图中的E区间
贴代码(含注释)

#include<bits/stdc++.h> using namespace std; #define ll long long #define pb push_back const int N = 2e5 + 10; pair<int , int>a[N << 1]; multiset<int>ha; int add[N]; int main() { int t; cin >> t; while(t --) { ha.clear(); memset(add , 0 , sizeof(add)); int n; cin >> n; for(int i = 1 ; i <= n ; i ++) { int l , r; cin >> l >> r; a[i * 2 - 1] = make_pair(l , -i); // second 为负代表 左端点 a[i * 2] = make_pair(r , i); // second 为正代表右端点 } a[2 * n + 1].second = 0; sort(a + 1 , a + 1 + 2 * n); int cnt = 0; // cnt 表示把所有区间合并后的区间个数 for(int i = 1 ; i <= 2 * n ; i ++) { if(a[i].second < 0) ha.insert(-a[i].second); if(a[i].second > 0) ha.erase(a[i].second); if(ha.size() == 0) // 表示某一段区间合并结束 cnt ++ ; if(ha.size() == 1 && a[i].second > 0 && a[i + 1].second < 0) ///对应博客中的 One add[*ha.begin()] ++; if(ha.size() == 1 && a[i].second < 0 && -a[i].second == a[i + 1].second) ///对应博客中的 Two add[*ha.begin()] = -1; } int ans = -(0x3f3f3f3f); for(int i = 1 ; i <= n ; i ++) ans = max(ans , add[i]); cout << ans + cnt << '\n'; } return 0; }
如果我的题解帮助了您,可否赏个赞呢



