力学笔记

2024.6.12：力学考炸了

2024.6.19：没完全炸

非惯性系中的动力学

直线加速参考系中的惯性力

惯性力\(F^*=-ma\)，惯性力不是相互作用，不存在反作用力，只有在非惯性系中能观察到惯性力

转动参考系

用极坐标推更简单，下面是笔者自己最开始的想法：

下面考虑在转动参考系中多出来的力

在惯性参考系下，位置矢量为\(\vec{r_t}=x_t\vec{i}+y_t\vec{j}+z_t\vec{k}\)

角速度为\(\vec{\omega}\)，在转动参考系中坐标轴单位向量分别为\(\vec{i_t}\)、\(\vec{j_t}\)、\(\vec{k_t}\)

转动参考系位置矢量为（下面仅讨论第一维）\(\vec{r_t'}=x_t(\vec{i}-\int \vec{\omega}\times\vec{i_t}dt)\)

\[\begin{aligned}\frac{d\vec{r_t'}}{dt}&=\frac{dx_t}{dt} (\vec{i}-\int \vec{\omega}\times\vec{i_t}dt)-x_t\cdot \vec{\omega}\times\vec{i_t}\\ \frac{d^2\vec{r_t'}}{dt^2}&=\frac{d^2x_t}{dt^2} (\vec{i}-\int \vec{\omega}\times\vec{i_t}dt)-2\frac{dx_t}{dt}\cdot \vec{\omega}\times\vec{i_t}-x_t\cdot \vec{\omega}\times(\vec{\omega}\times \vec{i_t} )\\ &=\frac{d^2x_t}{dt^2} (\vec{i}-\int \vec{\omega}\times\vec{i_t}dt)-2\frac{dx_t}{dt}\cdot \vec{\omega}\times\vec{i_t}+x_t\cdot |\vec{\omega}|^2\times \vec{i_t}\\ &=\frac{d^2x_t}{dt^2} (\vec{i}-\int \vec{\omega}\times\vec{i_t}dt)+2\frac{dx_t}{dt}\cdot \vec{i_t}\times\vec{\omega}+x_t\cdot |\vec{\omega}|^2\times \vec{i_t}\\ \end{aligned}\]

可设想有两个额外的力\(F_1=m\cdot (2\frac{dx_t}{dt}\cdot \vec{i_t}\times\vec{\omega})\)、\(F_2=m\cdot (|\vec{\omega}|^2\times \vec{i_t})\)

我们称有惯性离心力\(F^*=m\omega^2r\)（\(r\)为转动参考系的位置向量），科里奥利力\(F_K^*=2mv\times \omega\)（\(v\)是转动参考系中的速度）

角动量

质点对于参考点的位置矢量与其动量的矢积：\(L=r\times mv=r\times p\)称为质点对该参考点的角动量。

对于动量\(p\)，其对时间的导数\(\frac{dp}{dt}\)为力\(F\)
相对的，角动量对时间的导数

\[\begin{aligned} \frac{dL}{dt}=\frac{d(r\times mv)}{dt}=\frac{dr}{dt}\times mv+r\times \frac{d(mv)}{dt}=v\times mv+r\times F=r\times F \end{aligned}\]

我们称\(M=r\times F\)为力矩

刚体力学

定义转动惯量\(I=\sum m_ir_i^2\)，\(L=I\omega\)

平行轴定理：\(I=I_c+md^2\)

刚体定轴转动的转动定理：\(\sum M=I\alpha\)

万有引力

质心运动定理

质点系质量与质心加速度的乘积总是等于质点系所受一切外力的矢量和

如果单独考虑地球和月亮的运动，由于无外力，故质点不变，所以地月实际上是绕着质点在转动。

无滑滚动

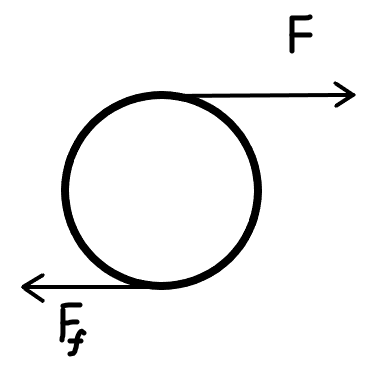
假设有拉力\(F\)以及摩擦力\(F_f\)，圆柱体无滑滚动（\(a=\alpha R\)），下面讨论其动能变化

由质心运动定理：

\[F-F_f=ma \]

由刚体定轴转动的转动定理：

\[(F+F_f)R=I_c\alpha \]

可得：

\[a=\frac{2F}{m+\frac{I_c}{R^2}} \]

故刚体动能为：

\[\begin{aligned} E_k&=\frac{1}{2}mv^2+\frac{1}{2}I_c\omega^2\\ &=\frac{1}{2}mv^2+\frac{1}{2}I_c\frac{v^2}{E^2}\\ &=\frac{1}{2}(m+\frac{I_c}{R^2})v^2\\ &=(m+\frac{I_c}{R^2})ax\\ &=2Fx\\ \end{aligned}\]

为何\(E_k=2Fx\)而不是\(Fx\)呢？

由于\(a=\alpha R\)，故\(F\)的作用点速度为质心速度的两倍，位移也为两倍

弹性体的应力和应变

应力：单位面积上受到的内力，单位：Pa

正应力：应力在面元外法线方向的投影，\(\sigma=\frac{F_n}{S}\)
切应力：应力在面元切向方向上的投影，\(\tau=\frac{F_{\tau}}{S}\)
线应变：\(\varepsilon=\frac{\Delta l}{l_0}\)
切应变：平行截面间相对滑动位移与截面垂直距离之比为剪切形变：\(\tan \gamma=\frac{\Delta x}{d}\)

拉/压形变的胡克定律

在应变较小时，应变与应力成正比

\(\sigma=E\varepsilon\)（\(E\)称为弹性模量，也称为杨氏模量）
又可表示为：\(\frac{F_n}{S}=E\frac{\Delta l}{l_0}\)。如果写成\(F_n=\frac{ES}{l_0}\Delta l=k\Delta l\)则为高中常见形式。

形变势能：\(A=\int_0^{\Delta l}\frac{ES}{l_0}x dx=\frac{ES}{l_0}\frac{1}{2}(\Delta l)^2=\frac{1}{2}E(\frac{\Delta l}{l_0})^2 Sl_0=\frac{1}{2}E\varepsilon^2 V\)

势能密度：\(E_p^0=A/V=\frac{1}{2}E\varepsilon^2\)

剪切形变的胡克定律

剪切形变的胡克定律：\(\tau=G\gamma\)

\(\gamma\approx \tan \gamma=\frac{\Delta x}{d}\)（\(G\)称为切变模量）

形变势能：
\(F=\frac{GS}{d}\Delta x\)
\(A=\frac{GS}{d}\int_0^{\Delta x}x dx=\frac{GS}{d}\frac{1}{2}(\Delta x)^2=\frac{1}{2}G(Sd)(\frac{\Delta x}{d})^2=\frac{1}{2}GV(\frac{\Delta x}{d})^2=\frac{1}{2}G\gamma ^2V\)

势能密度：\(E_p^0=A/V=\frac{1}{2}G\gamma^2\)

振动

\(\begin{aligned} &m\frac{d^2x}{dt^2}+kx=0\\ &\frac{d^2x}{dt^2}+\omega_0^2x=0（令\omega_0^2=\frac{k}{m}） \end{aligned}\)

解得\(x=A\cos(\omega_0t+\alpha)\)

\(\varphi=\omega_0t+\alpha\)叫做简谐振动的相位
两个振动的\(\varphi_1-\varphi_2\)称为相位差

波动和声

纵波方程为：

\[\frac{\partial^2y}{\partial t^2}=\frac{E}{\rho} \frac{\partial^2y}{\partial x^2} \]

张紧软绳的横波方程为：

\[\frac{\partial^2y}{\partial t^2}=\frac{F_T}{\rho_{线}} \frac{\partial^2y}{\partial x^2} \]

其中\(\rho_{线}S=\rho\)

平面简谐波方程：\(y=A\cos (\omega t\mp kx)\)（\(\omega=2\pi \nu\)，\(k=2\pi /\lambda\)）

\(\frac{\partial^2y}{\partial t^2}=-Ak^2v^2\cos k(vt-x)\)，\(\frac{\partial^2y}{\partial x^2}=-Ak^2\cos k(vt-x)\)

故有\(v_{横}=\sqrt{G/\rho}\)和\(v_{纵}=\sqrt{E/}\)

平面简谐波中的体元的振动和质点作简谐振动有什么不同？
体元振动的频率取决于波源的频率，而简谐振动的频率取决于系统本身性质

平面简谐波波速只与介质性质有关

速度\(u=\frac{\partial y}{\partial t}=-\omega A \sin( \omega(t-\frac{x}{v}))\)，动能\(dE_k=\frac{1}{2}\rho dVu^2\)

势能\(dE_p=dE_k\)，故\(dE=2dE_k=\rho dV \omega^2A^2\sin^2( \omega(t-\frac{x}{v}))\)

能量密度\(\varepsilon=dE/dV=\rho \omega^2A^2\sin^2( \omega(t-\frac{x}{v}))\)

\[\begin{aligned} \bar{\varepsilon}&=\frac{1}{T}\int_{0}^{T}\rho \omega^2A^2\sin^2( \omega(t-\frac{x}{v}))dt\\ &=\rho \omega^2A^2\frac{1}{T}\int_{0}^T \sin^2( \omega(t-\frac{x}{v}))dt\\ &=\rho \omega^2A^2\frac{1}{\omega T}\int_{0}^T \sin^2( \omega(t-\frac{x}{v}))d(\omega t)\\ &=\rho \omega^2A^2\frac{1}{\omega T}\int_{0}^{2\pi} \sin^2u du\\ &=\rho \omega^2A^2\frac{1}{\omega T}\pi\\ &=\frac{1}{2}\rho \omega^2A^2\\ \end{aligned}\]

平均能流密度（波的强度）：\(\bar{\varepsilon}v\)

波自波疏介质射向波密介质，反射波在相位上落后\(\pi\)，该现象称为半波损失

2. 多普勒效应：

假设波速为\(v\)，频率为\(\nu\)
设观测者向波源以\(v_{观}\)的速度走，波源向观测者以\(v_{源}\)的速度走（两速度参考系不同），则频率变化为\(\frac{v+v_{观}}{v-v_{源}}\nu\)

流体力学

静止流体

压强垂直于作用面

如果不垂直，则有沿作用面的切线有力，必破坏流体的平衡

一点的各个方向压强相等

\(p=p_0+\rho gh\)

狭义相对论

假设有一个惯性参考系\(K\)，在其中取一个空间直角坐标系Oxyz，并在各处安置一系列对\(K\)静止，且对\(K\)系来说是对准了的钟（称为\(K\)钟），在参考系\(K\)中一个事件用\((x,y,z,t)\)表示。
类似地，对于另一惯性参考系\(K'\)，也在各处安置一系列对\(K'\)系静止的，且对\(K'\)系来说是对准了的钟（\(K'\)钟），一个事件用\((x',y',z',t')\)。

\[x'=\frac{x-vt}{\sqrt{1-v^2/c^2}} \]

因为\(K\)系与\(K'\)系运动是相对的，将\(v\)换成\(-v\)，就有：

\[x=\frac{x'+vt'}{\sqrt{1-v^2/c^2}} \]

联立解出：

\[t'=\frac{t-xv/c^2}{\sqrt{1-v^2/c^2}} \]

相对论中的静止长度：在与物体相对静止的参考系中测量物体得到的长度

例题1：杆的静止长度为\(l_0\)，在\(S\)系中平行于\(x\)轴且以速率\(u\)沿\(x\)轴正向运动，求相对于\(S\)沿\(x\)轴正向以速率\(v\)运动的\(S'\)系中观测者测得的棒长。

假设\(S\)系中的事件设为\((x,t)\)，\(S'\)系中的事件设为\((x',t')\)

杆两端在\(S\)系中的坐标：\((ut,t)\)、\((ut+l_0\sqrt{1-u^2/c^2},t)\)（特别注意这里的\(l_0\)不再是原长）

\((x_1',t')\)对应\((x_1,t_1)\)，\((x_2',t')\)对应\((x_2,t_2)\)
有\(x_1'=\frac{x_1-vt_1}{\sqrt{1-\beta^2}}\),\(t'=\frac{t_1-vx_1/c^2}{\sqrt{1-\beta ^2}}\)
故\(x_2'-x_1'=\frac{(x_2-x_1)-v(t_2-t_1)}{\sqrt{1-\beta^2}}\)化简为\((x_2-x_1)\sqrt{1-\beta^2}\)

又\((1/u-v/c^2)x_1=\sqrt{1-\beta^2} t'\)，
\((1/u-v/c^2)x_2=\sqrt{1-\beta^2} t'+l_0\sqrt{1-u^2/c^2}/u\)

\(x_2'-x_1'=l_0\frac{\sqrt{(c^2-u^2)(c^2-v^2)}}{c^2-uv}\)

1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1