CF1450G
题意
有 \(n\) 名工人站成一排。用一个长度为 \(n\) 的字符串 \(s\) 表示他们的工作，其中第 \(i\) 个人的工作为\(s_i\)。给定一个有理数 \(k=\frac{a}{b}\)作为参数。
每次操作中，可以选择一个至少存在一名工人的工作 \(x\)。设所有工作为 xx 的工人的位置为 \(i_1,\dots,i_m(i_1<\dots< i_m)\)，若 \(k\cdot(i_m-i_1+1)\le m\)，则可以再选择另一个至少存在一名工人的工作 \(y\)，并将所有工作为 \(x\) 的人的工作替换成 \(y\)。
若可以通过若干次（含 \(0\) 次）操作将所有人的工作替换成 \(x\)，则称工作 \(x\) 是可达到的。求出所有可达到的工作。
\(1\le a\le b\le 10^5,n\le 5000\)，字符集大小\(\le 20\)，空间限制\(\text{32mb}\)。
做法
定义0：令\(C\)表示\(s\)中的字符集。
假设有一系列操作，最终字符转换为\(x\)。对于所有\(y\)转换为\(z\)的操作，让我们添加一条有向边\((y\rightarrow x)\)。其结构为一个以\(x\)为根的内向树。
定义1：对于一个字符\(y\)，用\(l_y\)表示第一次出现的位置，用\(r_y\)表示最后一次出现的位置。
定义2：对于任意非空的字符集合\(S\)，定义\(range(S)=[\min\limits_{y\in S}l_y,\max\limits_{y\in S}r_y]\)，定义\(cnt(S)\)为\(S\)中字符出现的次数。
对于有根树，对于非根节点\(y\)，令\(S_y\)表示\(y\)子树字符集，都满足：
定义3：对于树的每个节点，均满足以上条件，则称为有效树；对于一个森林的每个节点，均满足以上条件，则称为有效森林。
定义4：对于任意字符集\(M\)，令\(dp(M)\)为：\(M\)是否可以组成有效森林。
若\(dp(C\backslash\{x\})\)为真，则\(x\)可以成为答案。
两种转移
- 一棵树：\(M\)满足\((1)\)，且\(\exists y\in M,dp(M\backslash \{y\})\)为真，则\(dp(M)\)为真。
- 一个森林：\(M\)满足\((1)\)，且存在子集\(S\subset M\)使得\(dp(S)\)和\(dp(M\backslash S)\)为真，则\(dp(M)\)为真。
这样转移复杂度是\(O(3^{|C|})\)的。
观察：对于第二种转移，可以假设\(range(S)\cap range(M\backslash S)=\emptyset\)。
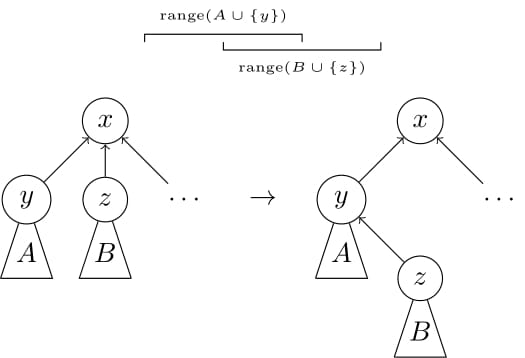
可以通过调整法，将有效树，转换为满足假设的有效树。
因为我们有：
\(\mathrm{cnt}(A\cup \{y\}\cup B\cup \{z\})= \mathrm{cnt}(A\cup \{y\})+\mathrm{cnt}(B\cup\{z\})\)
\(\ge k \cdot \left|\mathrm{range}(A\cup \{y\})\right| + k\cdot \left|\mathrm{range}(B\cup \{z\})\right|\ge k\cdot \left|\mathrm{range}(A\cup \{y\}\cup B\cup \{z\})\right|.\)
由此，第二种转移的个数缩减到了\(O(|C|2^{|C|})\)，可以通过此题。
