Codeforces Round #715 (Div. 1)

A

存在两个串，\(0\)的个数或者\(1\)的个数均大于\(n\)。
在\(0\)或\(1\)间把另外一个字符插进去。

B

结论：对于\(n\)阶排列，合法的方案数为\(2^{n-1}\)。

证明：
对于\(n\)阶排列，假设第一个位置填的是\(x\)，那么前缀会是\(x,x-1,\ldots,1\)。
令\(f_i\)为\(i\)阶排列合法方案数，\(f_0=1\)，有递推式：
\(f_n=\sum\limits_{i=1}^n f_{n-i}=2^{n-1}\)。

C

第五发才过...菜死了，我的做法相对较复杂，谨慎观看。

令\(w=\bigoplus\limits_{(u,v)\in E}w_{u,v}\)。

结论：存在最优解，需要填的边，除一条边权为\(w\)外，其他均为\(0\)。

证明：
若有两条边权不为\(0\)，将其中一条改变这两的异或，\(\text{MST}\)不会增大。

先搜出补图连通性：\(\text{cf920e}\)。

将补图连通的点先缩起来，用给出的边跑一个\(\text{MST}\)，用到的边权是必须用到的。

如果存在补图的某个连通块，边数\(\ge\)点数，那么在树的基础上将\(w\)放在另一条边，那么\(\text{MST}\)就为之前得到的。

那么现在要考虑补图的某条边边权为\(w\)，对\(\text{MST}\)的影响。
对于原图但不在\(\text{MST}\)的边，考虑其是否可能加入\(\text{MST}\)，将其与\(w\)取\(\min\)，在加上原\(\text{MST}\)，就为真正的\(\text{MST}\)。

• 如果其两端在补图中连通性相同，可以。
• 如果其两端在补图中连通性不同，其在\(\text{MST}\)中的路径如果存在补图的边，可以。

感觉讲得及其不清楚，就放下代码吧...

D

定义：点\(i\)简写为\(i\)，标签\(i\)简写为\(\hat{i}\)

观察1：对于\(a_i=i\)的点，若存在解，则一定存在没有操作过\(i\)的解。

证明：
若\(\hat{i}\)离开\(i\)，之后必定还要回到\(i\)，找到第一次离开\(i\)的操作与第一次回到\(i\)的操作，容易观察将这两次操作删除，不会对结果产生影响。

于是我们可以忽略所有\(a_i=i\)的所有点。

考虑如果一开始就是单轮换，该怎么做？

枚举任何一个点，作为中心，其他点与其连边。
这形成了一个菊花图，考虑中心的标签，将中心与上面标签数字的点交换，依次操作所有边后，显然合法。

但如果开始不是单轮换呢？
观察2：对于两个轮换，交换这两个轮换中任意两点的标签，会合并成一个轮换。

我们的大概思路是：将所有轮换合并成一个轮换，再将单轮换调整好。

我们依然枚举任意一个点，作为中心，对其他点极角排序，考虑相邻的两个点这种连边，即外围的蓝色边。
利用蓝色边，将多个轮换合并成一个轮换，这很容易实现。

但还有另外一种情况

如果选择的中心点在凸包上，是可能蓝色边与黄色边有交的。
考虑所有的点都在凸包上的情况。（否则选择不在凸包上的点，所有蓝色边有效）
但这样的蓝色边至多有一条，考虑是否可以忽略这条蓝边，以达到目的。
这相当于，对于一个凸包上的边，忽略两条相邻的边，是否可以通过其他边以达到目的，由于一个轮换至少有两个点，这是可行的。

综上，我们在\(O(n\log n)\)（极角排序），在最多\(1.5n\)次操作内解决了此问题。

E

定义：令点\(i\)上的标签为\(a_i\)。

总共\(n\)个过程，第\(i\)个过程为将\(i\)向下推。
在前\(i\)个过程结束后，将当前点的值\(\le i\)的看作绿色节点，其他的看作红色节点。

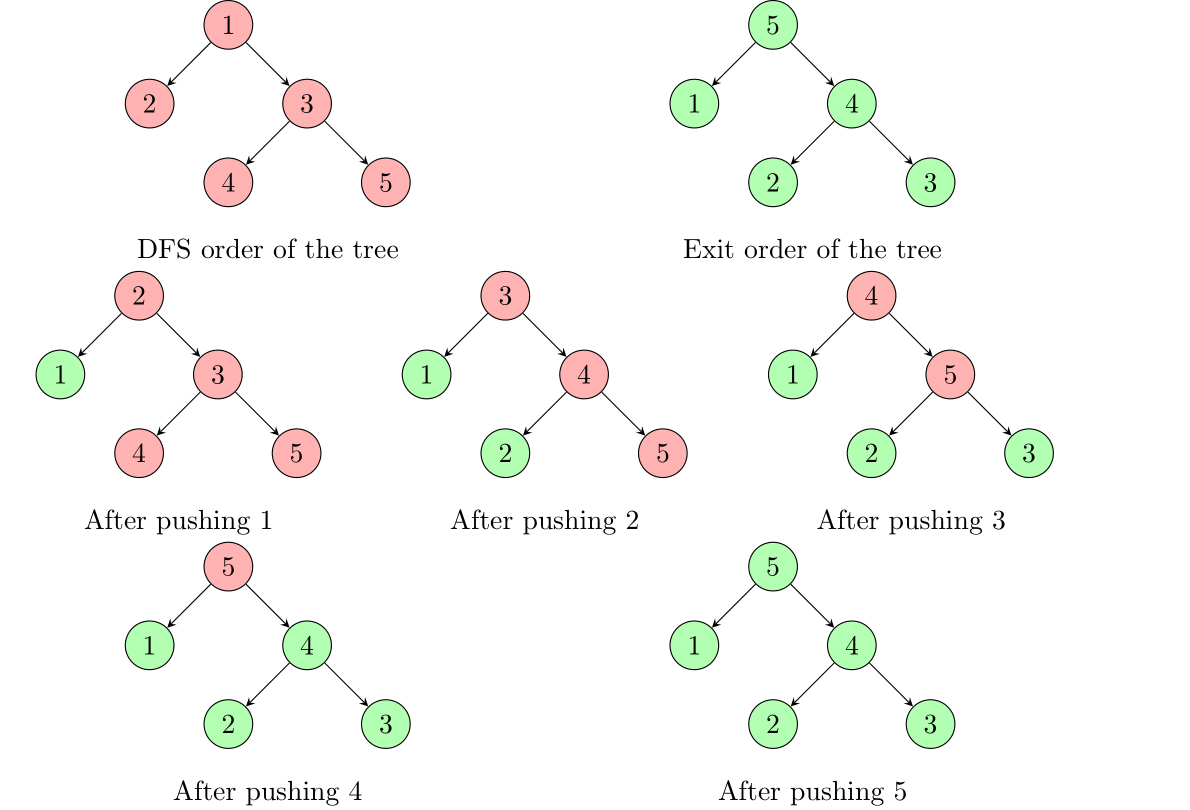
结论1：当前处在第\(\max(1,a_1-1)\)个过程。

结论2：在前\(i\)个过程结束后，红色节点值的相对顺序跟原来的相对顺序相同。

容易证明

推论：在任何时候，任意节点的子节点的值相对顺序不变。

结论3：在前\(i\)个过程结束后，经过的天数为现在点值为\(1\sim i\)的高度之和。

假设目前处在某一个过程恰好结束的时候，根据推论，容易求出所有绿点与红点的\(a_i\)。
假设目前处在过程\(dem=\max(i,a_1-1)\)，将\(a_i=dem\)的点移到根，以还原到前\(dem-1\)个过程恰好结束的时候。

考虑原来\(a_i=dem\)这个位置是否合法呢，找到最终\(a_j=dem\)的位置，判断\(j\)是否在\(i\)子树内即可。

感觉讲得非常不清楚...可以看下代码

F

题意：
给出一个\(n\)阶排列\(A\)，及\(q\)个区间\([l_i,r_i]\)。
定义排列\(B\)与\(A\)在\([l,r]\)相似，当且仅当在区间\([l,r]\)中，\(A\)和\(B\)的相对顺序相同。
定义排列\(B\)是\(\text{k}\)相似的，当且仅当对于\(1\le i\le k\)，\(B\)与\(A\)在\([l_i,r_i]\)均相似。
对于一个\(\text{DAG}\)图\(G\)，定义\(G\)是\(\text{k}\)相似的，当且仅当其拓扑序与\(\text{k}\)相似的排列一一对应。
输出\(q\)行，第\(k\)行输出\(\text{k}\)相似的图\(G\)的最小边数。
\(n\le 25000,q\le 100000\)。
时限：\(7s\)。

首先不考虑具体复杂度，可以构造出一个多项式复杂度算法：

对于目前的所有区间\([l_i,r_i]\)，对于每个区间\(l,r\)，令其长度为\(len=r-l+1\)，保留\(len-1\)条边（相对顺序相邻的点之间连边）。
然后对于有向边\((u,v)\)，若删掉\((u,v)\)后，\(u\)仍可以到达\(v\)则删除。

对于每个点，假设包含其的区间左端点最小为\(ld\)，包含其的区间右端点最大为\(rd\)。

与其相关的边至多有四条：
\([ld,i)\)中比其大的最小位置，比其小的最大位置
\((i,rd]\)中比其大的最小位置，比其小的最大位置
对于点对\((i,j)(i< j)\)，若其同时在\(i,j\)中都为相关的边，则保留，否则不保留。

正确性显然。

由于\(ld_i,rd_i\)增长的总次数为\(O(n^2)\)，故总复杂度\(O(n^2+q)\)。