jzoj5983

题意

给定\(n,m,k\)，求正\(n\)多边形中选\(m\)个点构成的凸包恰好有\(k\)个锐角的方案数。

做法

结论1：若\(k>4\)，则无解

证明：
凸多边形外角和等于\(360^{o}\)

结论2：若\(k=3\)，仅有可能\(m=3\)的时候可能有解

证明：
\(k=3\)时，若\(m>3\)，若有解，则会有两个锐角不相邻，选择一个，然后其底边的两端点与另一个三角形顶点连接。
显然这个四边形的对角和小于\(180^{o}\)，但正\(n\)多边形是能内接在圆内的，四边形的对角和为\(180^{o}\)

结论3：若选择\(3\)个点构成的三角形为钝角三角形，则一定存在某条直径是将三个点划分到同一侧的，且不会存在两个点恰好为直径的两端点

证明：
若所有直径三个点都不同侧，必然存在某条直径使得是将钝角顶点单独存在于一侧，根据直径与直角的那个性质结合调整法显然是不合理的

结论4：直径最多将正n多边形的\(\left\lfloor\frac{n}{2}\right\rfloor+1\)个点划分到同一侧

显然

• \(k=3,m=1\)，根据结论1、结论2****与结论3，有如下做法
  枚举某一点，在枚举另一点，显然两点间较短的圆弧上的所有点都能与其形成钝角三角形
  即一个点作为锐角的贡献为：\(\sum\limits_{i=1}^{\left\lfloor\frac{n}{2}\right\rfloor-1}i\)。然后还有些细节，就不讲了

• \(k=2\)，根据结论3，易得两个锐角是相邻的，有如下做法
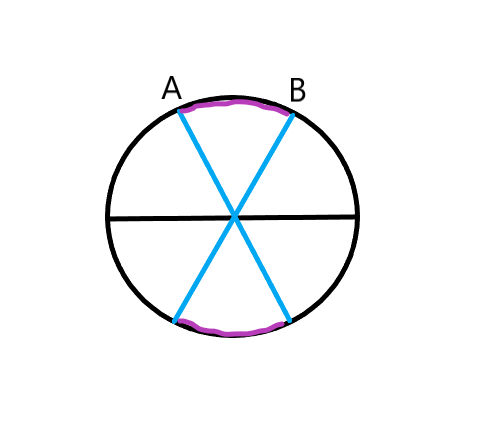
  假设顶点为\(A,B\)，如下图，显然剩下选择的点只能存在于紫色部分，且不能两个紫色均有点
  若\(m=3\)，显然不能选上面的
  然后就是二项式系数上指标求和
  

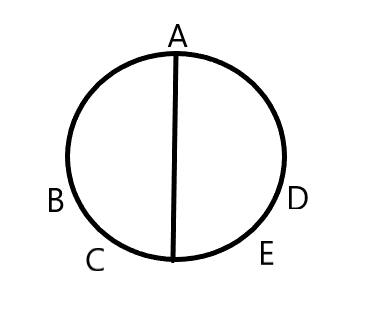
• \(k=1\)，根据结论3，令锐角为A，B与D的距离是被半圆限制的，为使得B与D不为锐角，还得存在两个点C与E分别存在于两个半圆
  可以这么做：枚举C与E中间的点个数，然后推一下式子