LeetCode 无序数组中的元素查找问题 数组问题
@
限定范围内的元素查找
41. 缺失的第一个正数 H
给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。Link
- 空间复杂度为O(n)的辅助数组解法
- 理论基础
- 1、假设数组中的元素个数为 n，则小于1的元素以及大于 n 的元素不会影响最小正整数的判断，因此此时最小正整数肯定取 1
- 2、[1, n] 区间范围内的正整数，其出现与否影响最小正整数的取值
- 实现思路
- 统计 [1, n] 区间范围内的正整数的出现情况，输出没出现的最小的正整数即可
- 1、若部分出现，输出第一个没出现的正整数
- 2、若全未出现，输出 1 即可
- 3、若全部出现，输出 n + 1 即可
- 1、2两种情况可进行合并，因为全未出现时，第一个没出现的正整数肯定为 1
class Solution {
public:
int minNumberDisappeared(vector<int>& nums) {
int n = nums.size();
vector<int> arr(n, 0);
for (int i = 0; i < n; i++) {
if (0 < nums[i] && nums[i] <= n) {
arr[nums[i] - 1] = nums[i]; // 记录有效区间范围内的正整数
}
}
for (int i = 0; i < n; i++) {
if (arr[i] != i + 1) return i + 1;
}
return n + 1;
}
};
- 空间复杂度为常数级别的原地置换方法
- 实现思路
- 1、将 [1, n] 区间范围内的正整数 num 交换至 num - 1位置
- 2、将 [1, n] 区间范围外的正整数、第 i 个位置的值为 i + 1 的情况均不做处理
- *若 [1, n] 区间范围内的正整数重复出现，可能会重复交换，陷入死循环，加条件判断：即判断其要交换的位置 i 是否满足值为 i + 1，若满足说明不用交换，直接跳过即可
- 3、重新遍历数组，第一个不满足位置 i 的值为 i + 1的时候，i + 1就是缺失的第一个正整数，如果均满足，则结果 n + 1
class Solution {
public:
int minNumberDisappeared(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n; i++) {
if (nums[i] == i + 1) continue;
// 数字在有效区间范围内，并且其要交换的位置还未得到合适的元素值
while (0 < nums[i] && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
swap(nums[i], nums[nums[i] - 1]);
}
}
for (int i = 0; i < n; i++) {
if (nums[i] != i + 1) return i + 1;
}
return n + 1;
}
};
287. 寻找重复数 M
给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。Link
- 将每个元素交换至其下标处，查找不符合对应条件的值即可
- 1、[1, n] 之间的值 i 交换至下标 i - 1处，除了重复值以外，其他元素均能一一对应
- 2、重新遍历数组，寻找不符合对应条件的那个值就是重复值
class Solution {
public:
int findRepeatNum(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n; i++) {
if (nums[i] == i + 1) continue;
while (nums[nums[i] - 1] != nums[i]) {
swap(nums[i], nums[nums[i] - 1]);
}
}
for (int i = 0; i < n; i++) {
if (nums[i] != i + 1) return nums[i];
}
return -1;
}
};
- 参考环形链表问题，不修改数组
- 1、建立下标和元素的映射关系，以 [1,3,4,2] 为例
- [1,3,4,2]
- [0,1,2,3]
- 从下标 0 开始，根据下标指向的元素遍历，则有 ‘0’ - 1 - 3 - 2 - 4 - NULL
- 2、若数组中存在重复的数字，则有
- [1,3,4,2,2]
- [0,1,2,3,4]
- 从下标 0 开始，则有 '0' - 1 - 3 - 2 - 4 - 2 - 4 - 2 ·····，进入死循环
- 3、类比环形链表的处理方法进行处理
- fast、slow 指向头节点 0
- fast 每次走两步，即 fast = nums[nums[fast]]
- slow 每次走一步，即 slow = nums[slow]
- 4、fast、slow相等则说明存在重复元素，即链表有环
- 5、fast 指向头节点，每次走一步，fast、slow再次相遇的位置即重复元素值，即入环点
class Solution {
public:
int findRepeatNum(vector<int>& nums) {
// 同一起点，快慢指针开始
int fast = 0, slow = 0;
fast = nums[nums[fast]];
slow = nums[slow];
while (slow != fast) {
fast = nums[nums[fast]];
slow = nums[slow];
}
// 找到入环点，即重复元素
fast = 0;
while (fast != slow) {
fast = nums[fast];
slow = nums[slow];
}
return fast;
}
};
与出现次数相关的元素查找
136. 只出现一次的数字
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。Link
- 位运算、异或
- 1、两个相同的数异或结果为0
- 2、一个数与 0 异或结果不变
- 3、使用 0 与数组中的所有数异或，最终结果就是出现一次的数字
int singleNumber(vector<int>& nums) {
int x = 0;
for (auto & num : nums) {
x = x ^ num;
}
return x;
}
260. 只出现一次的数字 III
给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。Link
- 位运算
- 假设两个出现一次的元素为 x、y，则数组所有数字异或的结果就等于 x ^ y，记为 z
- 1、z 中所有为 1 的位置是 x 或 y 中所独有的 1，取 mask 为 z 中第一个 1，这个 1 为 x 或 y 所独有的
- 2、利用数字与 mask 相与的结果分成两组，这样 x、y 可以落进不同的组中，转化为 260题的求解方式
-
& 的优先级低于 ==
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
int z = 0;
for (auto &num : nums) {
z ^= num;
}
int mask = 1;
// & 优先级低于 ==，此处必须对位运算的结果加括号
while ((mask & z) == 0) {
mask = mask << 1;
}
int x = 0, y = 0;
for (auto &num : nums) {
if ((num & mask) != 0) x ^= num;
else y ^= num;
}
return {x, y};
}
};
137. 只出现一次的数字 II
给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。Link
- 位运算
- 三个相同的数字，统计每一个二进制位上 1 的个数，必定为 3 的整数倍，对 3 取余便是只出现一次的那个二进制位，组合结果便为只出现一次的数字
- 1、统计每个二进制位上 1 的个数
- 2、对 3 取余，然后赋值给结果对应的二进制位上
class Solution {
public:
int singleNumber(vector<int>& nums) {
vector<int> cnt(32, 0);
for (int i = 0; i < nums.size(); i++) {
int num = nums[i];
unsigned int flag = 1;
for (int i = 31; i >= 0; i--) {
if ((num & flag) != 0) {
cnt[i]++;
}
flag = flag << 1;
}
}
int ans = 0;
for (int i = 0; i < 32; i++) {
ans = ans << 1;
ans = ans | (cnt[i] % 3);
}
return ans;
}
};
- 一种简化的版本：即求即算
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = 0;
for (int i = 0; i < 32; i++) {
int cnt = 0;
for (int num : nums) {
cnt += (num >> i) & 1;
}
if (cnt % 3) {
ans |= (1 << i);
}
}
return ans;
}
};
-
数字电路、状态机
-
1、各二进制位上 1 的个数除以 3 的余数共有三种状态：0、1、2，状态转换如图
-
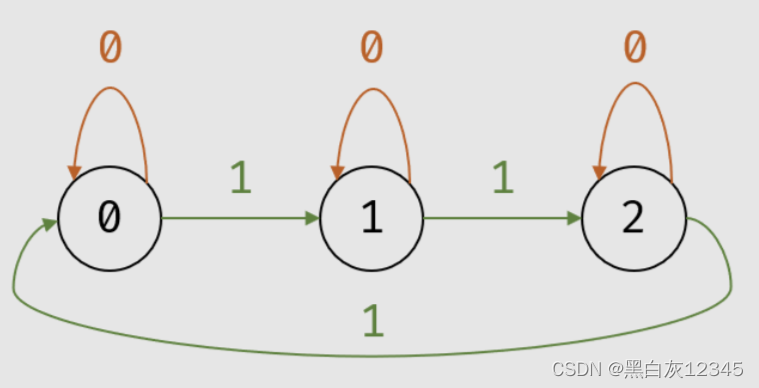
2、用两个比特 b a 表示这 3 种状态，即
-
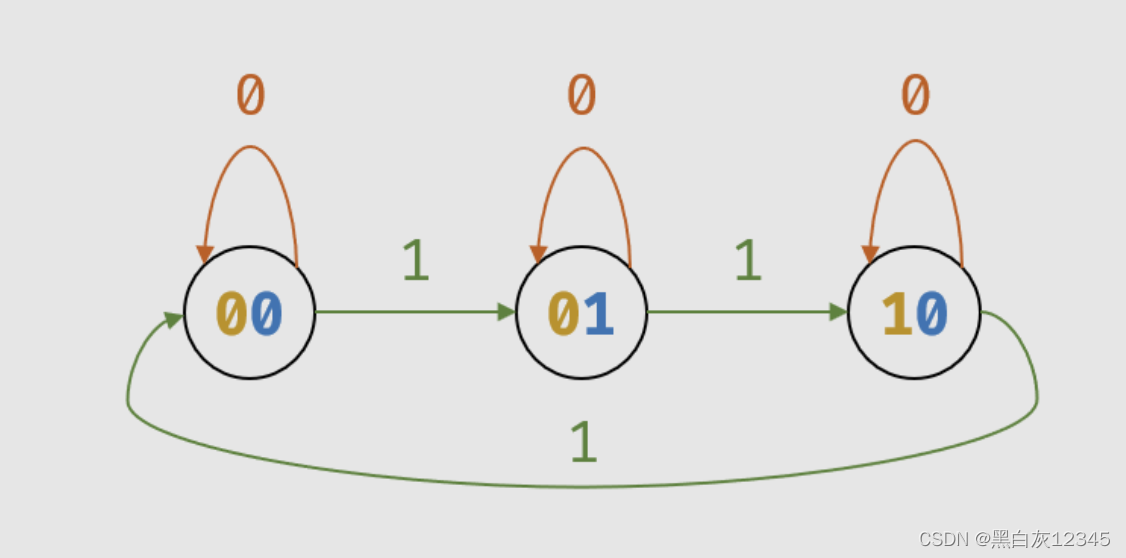
3、首先计算低位比特 a 的更新情况：a = a ^ x & ~b
-
4、比特 a 更新结束以后的状态转换为(假定输入 x 均为 1)
-
5、将 b a 的位置对调，并调整状态位置
-
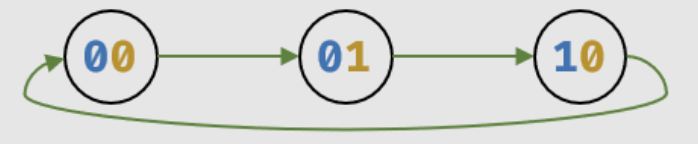
5、比特 b 的更新情况与 a 相同：b = b ^ x & ~ a
-
6、其与二进制位的更新情况相同
-
7、遍历结束，各二进制位的状态为 0 或 1，即 00、01，是由比特 a 记录的，因此返回 a 即可。
图片引用自LeetCode K神的题解，Link
class Solution {
public:
int singleNumber(vector<int>& nums) {
int b = 0, a = 0;
for (int x : nums) {
a = a ^ x & ~b;
b = b ^ x & ~a;
}
return a;
}
};
