这篇记录的内容来自于Andrew Ng教授在coursera网站上的授课。
1.不要浪费大量的时间在获得样本上。实际上,太多的样本数并不会使学习算法更加的优秀。要尝试调整你的系数:
1.使用更少的特征。
2.增加多项式。
3.调整$\lambda$。
2.诊断学习算法:
1.将样本打乱,并将其中一部分作为训练样本,剩下的作为测试样本,来判断是否出现了过拟合。
2.将样本划分为三类:训练集,交叉验证(cross validation,cv)集,测试集。对于线性回归,训练集来得出相应次数下的theta,交叉验证集来比较这些theta,获得最好的模型,测试集继续训练模型。
1.支持向量机(support vector machine,SVM):一种监督分类模型。它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,最终转化为一个凸二次规划问题来求解。
cost函数:$cost_1(x)=max(0,-\theta^{T}x+1)$
$cost_0(x)=max(0,\theta^{T}x+1)$
J函数:$J_{\theta}(x)=\sum_{i=1}^{m}(y^{(i)}cost_1(\theta^{T}x^{(i)})+(1-y^{(i)})cost_0(\theta^{T}x^{(i)}))+\lambda\sum_{i=1}^{n}{\theta_i^2}$
h函数:$h_{\theta}(x)=\begin{cases}1\quad if\quad \theta^{T}x\geq0\\0\quad otherwise\end{cases}$
直观感受:
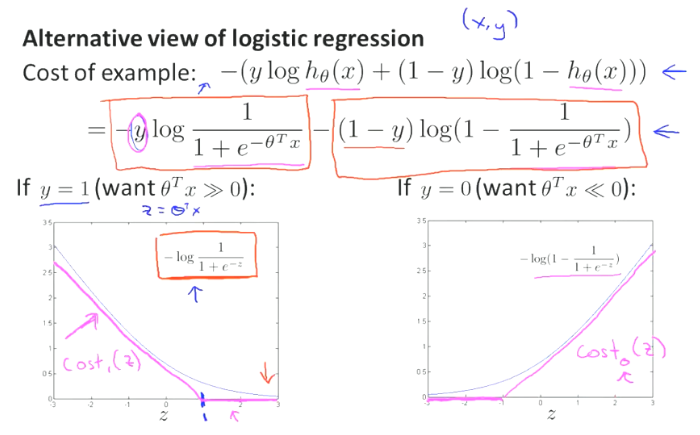
若y=0,只有cost0起作用,即右边的图,让它越往左越好。
若y=1,只有cost1起作用,即左边的图,让它越往右越好。
SVM在做什么?
直观感受:
对于逻辑回归,如果我们对以下样本进行分类,画出的决策边界可能是这样的:
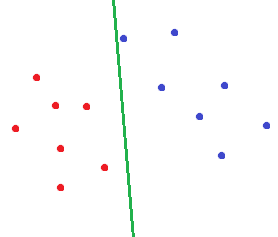
而对于SVM,会画出这样的决策边界: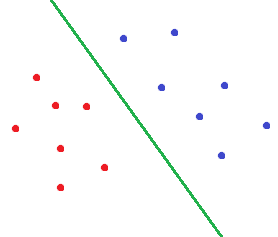
很明显,第二种决策边界是符合人的审美的。而这也就是间隔最大化。
为什么会这样?
我们容易发现,theta是这个超平面的法向量,内积的运算可以转化为矩阵乘法,相当于这里的$\theta^{T}x$,也等于到法向量的距离乘上“法向量”的模长(有符号)。正则项也可以看成是这个“法向量”模长的平方。
举例来讲,我们有以下两种情况:
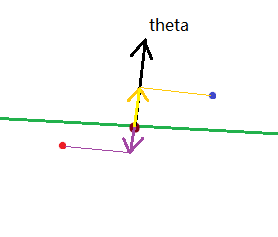
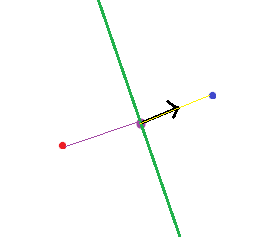
对于前一种情况,如果每个样本到超平面的距离都一定,我们就想要使法向量的模长尽可能大(这样才能对应于标签,减小代价函数的前一项)。但这时正则化项的代价也会上升,两者是相矛盾的。
对于后一种情况,法向量会尽可能缩小样本到它的距离,这样“法向量”的模长就能够减小了,同时正则化项的代价也会下降,两者是不矛盾的。
由此可见,缩小样本到法向量的距离、分开这两种类别是SVM的第一选择。
2.高斯核函数(Gaussian kernal):
记号:
$f_i$:第i个特征组合,为了方便表示像x1x2,x1x2x3这样的式子。
$K(x,l^{(i)})=exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2})$

 posted on
posted on

