这篇记录的内容来自于Andrew Ng教授在coursera网站上的授课。
1.多元线性回归(multivariate linear regression):
h函数:$h_{\theta}{(x)}=\theta_{0}+\sum_{i=1}^{n}{\theta_{i}x_{i}}$
为方便起见,每个样本的维度都设为n+1维,每一维都向后延一位,第一维是1。
则$$h_{\theta}{(x)}=\sum_{i=0}^{n}{\theta_{i}x_{i}}$$
$$h_{\theta}{(x)}={\theta}^{T}x$$
J函数为平方误差函数。
最小化$\frac{1}{2m}\sum_{i=1}^{m}{(h_{\theta}(x^{(i)})-y^{(i)})^2}$。
多元线性回归的梯度下降法:
$\theta_{i}:=\theta_{i}-\alpha\frac{1}{m}\sum_{j=1}^{m}{(h_{\theta}(x^{(j)})-y^{(j)})}x^{(j)}_{i}$
2.特征缩放(feature scaling):在梯度下降时有时会因为样本的某些特征相差了几个数量级,在一个区域内反复振荡,速度很慢。
让这些特征保持在一个相近的范围内了来提高速度,就是特征缩放。
范围不能太大,也不能太小。这只是一个实践性的结论。
使用特征缩放后的拟合函数来进行预测时,新的样本也要缩放一下。
3.均值归一化(mean normalization):对于特征缩放,考虑$$x^{(i)}:=\frac{x^{(i)}-\mu}{S}$$其中mu是平均值,S是最大值减去最小值,
1.梯度下降中学习率不要太大(发散),不要太小(太慢)。
若要求选取学习率,可以尝试将某些数量级的a试一遍。
学习率太大了:
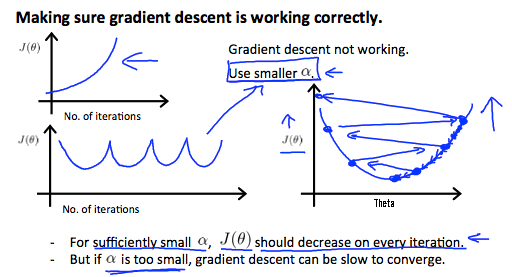
学习率太小了:

1.多项式回归(polynomial regression):$h_{\theta}{(x)}=\sum_{i=0}^{n}{\theta_{i}x_{i}^{i}}$。这里只有一个变量。
2.对于多项式回归,可以变为多元线性回归,但要注意特征缩放。
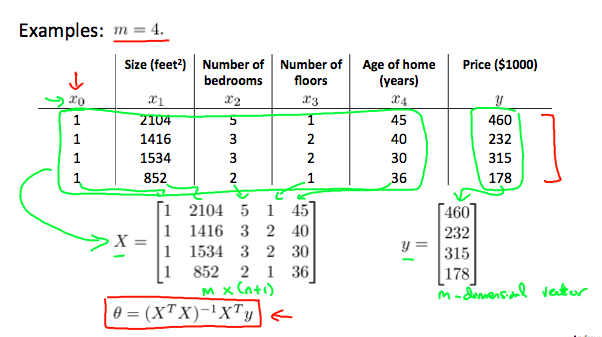
1.标准方程法:多元线性回归的精确解。$\theta=(X^TX)^{-1}X^TY$
Octave:pinv(X'*X)*X'*Y
如何构造X、Y:X为m样本的转置放在一个矩阵中,y就是样本的标签的向量。
证明:http://www.mamicode.com/info-detail-2662773.html
矩阵不可逆?:https://blog.csdn.net/DataAnalyst_ing/article/details/85859226
与梯度下降的比较:样本较少时,标准方程法快;样本较多时,梯度下降快。
标准方程得出的是精确解,梯度下降得出的是近似解。
python实现的多项式回归:
能自动调次数,有均值归一化。

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 import scipy.optimize as opt 5 import math 6 #############################方便起见,一个样本是一行n列的,theta也是一行n列的。 7 path="ex1data3.txt" 8 degree=11 9 ######################################################################代价 10 def cost(theta,x,y): 11 theta=np.matrix(theta) 12 x=np.matrix(x) 13 y=np.matrix(y) 14 z=np.power((x*theta.T-y),2) 15 return np.sum(z)/(2*len(x))###平方误差函数 16 ######################################################################更新函数 17 def gradient(theta,x,y): 18 theta=np.matrix(theta) 19 x=np.matrix(x) 20 y=np.matrix(y) 21 error=x*theta.T-y 22 m=x.shape[0] 23 n=x.shape[1] 24 temp=np.zeros(n) 25 for i in range(n): 26 z=np.multiply(error,x[:,i]) 27 temp[i]=np.sum(z)/m###梯度下降 28 return temp 29 ######################################################################处理数据 30 def process(data): 31 x=data.iloc[:,0] 32 now=x 33 data2=pd.DataFrame(np.zeros((data.shape[0],degree))) 34 mean=np.zeros(degree+2) 35 len=np.zeros(degree+2)###n+1项加上输出的1项。 36 for i in range(degree): 37 mean[i+1]=np.mean(now) 38 len[i+1]=now.max()-now.min()+1###计算平均值和差值,+1是防止除0。 39 data2[i]=(now-mean[i+1])/len[i+1] 40 now=now*x 41 x=data.iloc[:,1] 42 mean[degree+1]=np.mean(x) 43 len[degree+1]=x.max()-x.min()+1 44 data2[degree+1]=(x-mean[degree+1])/len[degree+1] 45 mean[0]=1 46 len[0]=1 47 return data2,mean,len 48 ######################################################################决策边界 49 def getBoundary(vector,L,R,mean,len): 50 x=np.linspace(L,R,100) 51 f=np.linspace(L,R,100) 52 for i in range(100): 53 sum=0 54 for j in range(degree+1): 55 k=degree-j 56 if(k==0): 57 sum+=vector[k]###theta_0不需要变化。 58 else: 59 sum+=vector[k]*(math.pow(x[i],k)-mean[k])/len[k] 60 f[i]=sum*len[degree+1]+mean[degree+1]###倒推 61 return x,f 62 ######################################################################主函数 63 def main(): 64 ################读入数据并处理 65 source=pd.read_csv(path,header=None,names=["population","profit"]) 66 data,mean,len=process(source) 67 data.insert(0,"Ones",1) 68 x=np.matrix(data.iloc[:,0:degree+1]) 69 y=np.matrix(data.iloc[:,degree+1:degree+2]) 70 vector=np.zeros(degree+1) 71 ################梯度下降 72 vector=opt.fmin_tnc(func=cost,x0=vector,fprime=gradient,args=(x,y))[0] 73 print(vector) 74 print(mean) 75 print(len) 76 #################画图 77 x,f=getBoundary(vector,source.population.min(),source.population.max(),mean,len) 78 fig,ax=plt.subplots(figsize=(12,8))###看清楚了 79 ax.plot(x,f,"r",label="prediction") 80 ax.scatter(source.population,source.profit,label="data") 81 ax.set_xlabel("population") 82 ax.set_ylabel("profit") 83 ax.set_title("Polynominal Regression") 84 plt.show() 85 ###################################################################### 86 if __name__=="__main__": 87 main()



 posted on
posted on
